Starea de echilibru stabil

Se spune despre un corp solid că se află în echilibru stabil dacă, după ce asupra lui intervine o perturbare exterioară modificându-i echilibrul, această modificare este eliminată prin simpla încetare a acţiunii elementului perturbator, încât corpul revine în starea iniţială.
În cazul barelor drepte solicitate la compresiune, dacă secţiunile lor transversale au dimensiuni relativ mici faţă de lungime, atunci axele lor tind să se curbeze şi forţele axiale care le încarcă produc îndoirea barelor, cu intensitate proporţională cu mărimile forţelor. Atunci când încărcările ating un anumit nivel (denumit critic), deformaţiile de încovoiere cresc peste limita de suportabilitate a barei, care cedează instantaneu, desigur nu din cauza depăşirii limitelor de rezistenţă ale materialului său, ci datorită unei stări de deformareelastică instabilă.

Fenomenul de flambaj longitudinal

În cazuri precum cel de mai sus nu este vorba despre cedarea sub o solicitare propriu-zisă, ci despre un fenomen particular, denumit flambaj, care are consecinţe catastrofale şi trebuie evitat. Fenomenul este periculos deoarece este ireversibil şi nu este pe deplin stăpânit prin metode de calcul. Ceea ce se poate stabili este doar nivelul solicitării critice (Fcr), având valori specifice fiecărei bare concrete; se admite că pentru încărcările mai mici decât acest nivel flambajul barei respective nu se produce.
Din necesităţi de calcul se defineşte şi tensiunea critică de flambaj (scr) a unei bare – tensiunea normală ce corespunde sarcinii ei critice. Este interesant că această tensiune se poate afla sub limita de proporţionalitate (sau de elasticitate) a materialului, caz numit flambaj elastic al barei, dar poate fi şi deasupra acestei limite – pentru care flambajul este elasto-plastic.

Problema flambajului elastic al barelor drepte a fost rezolvată, în privinţa calculelor, încă de la mijlocul secolului XVIII, de către savantul elveţian Leonard Euler. În schimb, pentru flambajul elasto-plastic, deşi s-au stabilit diferite soluţii teoretice, acestea au un caracter predominant empiric, fiind adică bazate exclusiv pe observaţiile experimentale.
Ideea fundamentală în calculele de flambaj este aceea că solicitarea reală (Fef) trebuie să se afle la o anumită distanţă (de siguranţă) faţă de sarcina critică (Fcr) a barei analizate. Această condiţie implică stabilirea unei valori minime impuse a raportului dintre cele două niveluri de încărcare, sub forma unui coeficient de siguranţă la flambaj (c). Această mărime poate fi definită atât în legătură cu forţele F, cât şi cu tensiunile normale, astfel:

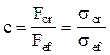                                      (1.1)

Coeficientul de siguranţă la flambaj este întotdeauna supraunitar, cu atât mai mare cu cât piesa este mai importantă la locul de utilizare sau în ansamblul din care face parte. Pentru corpurile de tip bară întâlnite în construcţiile de maşini valorile coeficientului se admit a fi cuprinse între 2,5 şi 28, dar în mod obişnuit el se limitează la 3-4 unităţi.

Calculul forţei critice în cazul flambajului elastic

Spre deosebire de calculele obişnuite de rezistenţă, calculele de stabilitate pornesc de la efectele fenomenului de flambaj către cauzele sale. Din acest motiv rezolvările au în vedere, în multe aspecte ale studierii fenomenului, cazuri particulare de producere a lui.
În privinţa flambajului elastic (pentru care scr este sub limita de proporţionalitate sp de pe curba caracteristică la compresiune a materialului barei) analiza porneşte de la apariţia solicitării de încovoiere pe barele comprimate lungi şi subţiri. Scriind ecuaţia fibrei medii (stabilită tot de Euler) pentru bara astfel deformată, se obţine o ecuaţie diferenţială, specifică modului în care este rezemată bara. Rezolvarea ecuaţiei, pe baza condiţiilor la limită, conduce la aflarea forţei critice de flambaj.

Fig. 1.1

Cazul barei articulate la ambele capete

Starea deformată a barei din fig. 1.1 indică apariţia, în orice secţiune transversală, a unui moment de încovoiere de forma
Miz(x) = F×v(x).
Prin urmare, ecuaţia lui Euler se poate scrie, pentru această stare de încărcare, astfel:

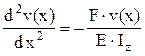                                         (1.2)

Dacă se trec toţi termenii în membrul stâng şi se face notaţia

                                                 (1.3)

atunci ecuaţia devine:      

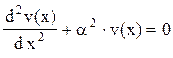
Soluţia acestei ecuaţii diferenţiale trebuie să fie de forma
v(x) = A sin ax + B cos ax ,
iar coeficienţii se pot determina impunând condiţiile de deformabilitate a barei (condiţiile la limită), date în acest caz de împiedicarea deplasării ei pe verticală în secţiunile de la capete:

Ultima condiţie rezultă din cerinţa de a se evita soluţia banală a ecuaţiei diferenţiale, v(x)=0, iar constanta k poate fi orice număr natural (diferit de zero). Dacă se ia în considerare prima soluţie posibilă (k=1), rezultă că bara deformată are aspect de sinusoidă, având ecuaţia:

Trebuie observat că în această expresie valoarea maximă (v max) a deplasării rămâne nedeterminată, ceea ce menţine posibilitatea de evoluţie catastrofală a fenomenului de flambaj.
Din condiţia (a×L=p) rezultă valoarea constantei a, care se poate înlocui în relaţia (1.3), astfel:
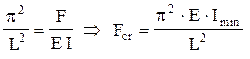                     (1.4)

Introducerea lui I min (cel mai mic dintre momentele de inerţie principale centrale ale secţiunii transversale) în formulă conduce la cea mai mică dintre posibilele forţe critice de flambaj ale barei studiate. De altfel, este uşor de intuit că încovoierea barei (sub forţă axială) se produce în mod preferenţial în jurul axei principale centrale (a secţiunii transversale) față de care momentul de inerţie (adică rezistenţa la încovoiere) are valoare minimă.
Relaţia (1.4), numită şi formula lui Euler pentru cazul fundamental de flambaj, se foloseşte la calculul forţei critice pentru bara comprimată ca în figura 1.1 de mai sus.
Atenţie: Forţa critică este nivelul solicitării de compresiune până la care se admite că nu se produce pierderea stabilităţii elastice a barei, adică trebuie evitate încărcările ce ar atinge această limită!

Desigur că se pot scrie noi soluţii ale ecuaţiei diferenţiale (1.2), dând lui k alte valori decât 1; dacă se adoptă k=2, se obţine că (a×L=2p) şi se ajunge la a doua forţă critică a barei:
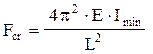                                        (1.5)

Această valoare corespunde situaţiei în care lungimea barei se înjumătăţeşte prin rezemare suplimentară, la mijlocul lungimii sale, cu o articulaţie mobilă (fig. 1.2); se observă că noua variantă de rezemare este o soluţie practică relativ simplă pentru a mări (de 4 ori) forţa critică de flambaj a barei, deci şi intervalul de funcţionare sigură a ei.
Pentru următoarele soluţii ale ecuaţiei diferenţiale (obţinute din condiţia a×L=kp) se deduce, cu un raţionament asemănător, că se introduc un număr de (k–1) reazeme mobile intermediare, obţinând creşterea de (k2) ori a forţei critice a barei. Trebuie însă observat că orice defectare a unuia sau unora dintre reazeme duce la scăderi importante ale forţei critice!

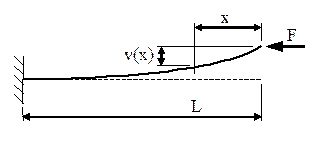Fig. 1.3

Calculul forţei critice pentru alte cazuri de rezemare

Pentru bara în consolă (fig. 1.3) se remarcă faptul că axa longi-tudinală se curbează rămânând tangentă la poziţia din momentul anterior producerii solicitării.
Efortul secţional de încovoiere se calculează la fel ca la bara articulată la capete:
Miz(x) = F×v(x).

Prin urmare, ecuaţia diferenţială a fibrei deformate se scrie tot sub forma (1.2) şi întregul raţionament făcut anterior se repetă aici, iar singura deose-bire apare în scrierea condiţiilor la limită (după cum s-a ales originea coor-donatei x, rezultă că sunt egale cu zero săgeata barei – în x=0 şi respectiv rotirea ei – în x=L):

Pentru cea de-a doua condiţie se observă că nici constanta A (care ar însemna că bara nu se curbează deloc) şi nici parametrul a nu pot fi nule, iar din egalitatea cu zero a funcţiei trigonometrice rezultă că argumentul ei trebuie să fie multiplu impar de (p/2). Folosind prima valoare posibilă, adică aL = p/2,  se ajunge la:

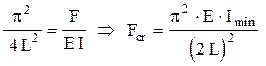                              (1.6)

   adică formula forţei critice de flambaj pentru bara în consolă.
Procedând analog (cu ecuaţii diferenţiale neomogene) se pot rezolva încă două cazuri de rezemare pentru barele comprimate – încastrare la ambele capete (fig. 1.4), respectiv încastrare la un capăt şi articulaţie la celălalt (fig. 1.5). Forţa critică se calculează, pentru fiecare caz, cu relaţia scrisă în dreptul figurii respective.

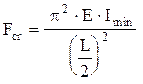  (1.7)

  (1.8)

Analizând relaţiile forţei critice pentru cazurile de rezemare studiate, se observă că ele se diferenţiază prin mărimea de la numitor; această mărime se notează cu (Lf2), desemnând “lungimea de flambaj” a barei pentru fiecare variantă de încărcare. Din relaţiile de mai sus se extrag lungimile de flambaj pentru situaţiile respective, astfel:

• pentru bara dublu articulată                   Lf = L
• pentru bara în consolă                            Lf = 2L
• pentru bara dublu încastrată                  Lf = L/2
• pentru bara articulată şi încastrată        Lf = 0,707×L

În acest mod se ajunge la o formă unică a relaţiei lui Euler, pentru calculul forţei critice în cele patru tipuri de rezemare:
                                            (1.9)
Observaţii:

1. Pentru toate discuţiile de faţă se admite că factorul EI (rigiditatea barei la încovoiere) este constant pe lungimea L a barei studiate, iar această lungime este practic egală, în starea deformată, cu cea iniţială! În plus, greutatea proprie a barei se neglijează.
2. Prezenţa la numitor a lungimii de flambaj arată că barele cu lungimi mari au forţe critice mici, deci un pericol mare de cedare prin flambaj.
3. Din compararea valorilor Lf pentru cele 4 cazuri de rezemare rezultă că bara în consolă se află în situaţia cea mai periculoasă, având cea mai mare lungime de flambaj (Lf = 2L), cea mai sigură fiind bara dublu încastrată (Lf = L/2).
4. Pentru barele care flambează elastic forţa critică depinde, în raport cu materialul barei, numai de modulul de elasticitate E, iar acesta are valori similare pentru cele mai multe oţeluri. Din acest motiv, pentru astfel de bare (la care flambajul este ameninţarea principală) nu este raţional să se folosească oţeluri aliate, care sunt scumpe, ele se fac din oţeluri laminate obişnuite!
5. Forţa critică a unei bare creşte proporţional cu momentul de inerţie al secţiunii sale faţă de axa de încovoiere. Secţiunile cele mai avantajoase sunt cele cu materialul dispus simetric (astfel ca Iz = Iy) şi la distanţă cât mai mare de axele de simetrie, pentru ca momentul de inerţie să fie maxim, la un consum de material dat.

Aplicabilitatea formulei lui Euler

S-a precizat că în toate cazurile de mai sus flambajul barelor este de tip elastic: pierderea stabilităţii tinde să se producă în domeniul deformabilităţii elastice a materialului barei, în care tensiunea maximă din piesă nu depăşeşte limita de proporţionalitate (sp) de pe curba caracteristică.
Dacă se defineşte, pe baza forţei critice dată de formula (1.9), o tensiune critică de flambaj scr (ca raport între forţa critică şi aria secţiunii transversale a barei), ţinând seama de relaţia de definiţie a razei de inerţie               rezultă că:
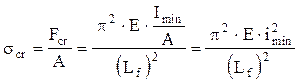                                   (1.10)
Această relaţie devine mult mai simplă dacă se face notaţia

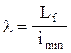    (1.11)
adică                     

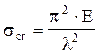                                                       (1.12)
Numărul l, coeficientul de subţirime (sau de zvelteţe) al barei analizate, este raportul între două lungimi (nu are dimensiuni!) şi reprezintă indicatorul principal al modului în care o bară concretă se calculează la flambaj.

Observaţii:

• Calculele de stabilitate elastică sunt specifice fiecărei bare, inclusiv în privinţa materialului şi încărcărilor ei.
• Coeficientul l introduce în calculele de flambaj influenţele exercitate asupra stabilităţii barei de lungimea, rezemarea, dar şi de forma şi dimensiunile secţiunii ei transversale.
• Două bare caracterizate prin aceeaşi valoare a coeficientului de subţirime îşi vor pierde stabilitatea elastică în acelaşi fel.

Pornind de la relaţia (1.12) se poate construi o curbă de dependenţă între tensiunea critică de flambaj şi coeficientul l. Principial, graficul acestei funcţii reprezintă o hiperbolă echilateră, dar trebuie remarcat că numai o porţiune din acest grafic este relevantă pentru calculul barei: deoarece relaţia (1.12) se referă la flambajul elastic, rezultă că forma hiperbolică a graficului (fig. 1.6) este valabilă numai în zona aflată sub limita de proporţionalitate a materialului (scr<sp). Graniţa acestei zone pe axa absciselor depinde exclusiv de caracteristicile materialului barei şi se obţine extrăgând din relaţia (1.12) valoarea lui l ce corespunde tensiunii limită sp:
                                     (1.13)

Prin urmare, deşi coeficientul l ţine seama în mod complex de bara concretă, graniţa l0 a domeniului în care bara se calculează cu formula lui Euler este dată numai de materialul barei; de exemplu, pentru oţelul laminat OL37 (având sp=190 şi E=21×104 [MPa]) această graniţă va fi:
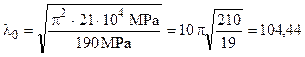                      (1.14)
Pentru calculele uzuale această valoare se admite a fi l0@105. Domeniul de pe grafic (fig. 1.6) aflat la dreapta acestei graniţe este pentru flambajul elastic, cel de la stânga urmând să descrie dependenţa dintre tensiunea critică şi coeficientul l în cazurile de flambaj elasto-plastic.
Observaţii:

• Pentru fiecare bară şi mod de rezemare există o singură valoare a lui l, deci oricărei situaţii concrete de încărcare îi corespunde un punct reprezentativ pe axa absciselor din graficul de mai jos; poziţia lui arată cum se fac calculele de stabilitate longitudinală pentru bara studiată!
• Cu cât materialul barei are o valoare mai mare a lui sp, cu atât valoarea limitei l0 va fi mai mică, adică domeniul în care bara flambează elastic va fi mai întins!

Trebuie observat şi că valoarea lui l este cu atât mai mare cu cât bara este mai zveltă (adică mai lungă faţă de dimensiunile transversale). Figura 1.6 arată că, dacă l creşte foarte mult, domeniul încărcărilor permise scade drastic, iar bara nu mai poate fi, practic, încărcată cu forţe de compresiune.
Rezultă că domeniul real de flambaj elastic trebuie limitat şi în partea sa dreaptă: barele nu pot avea coeficientul de subţirime mai mare decât un anume l2, ales în funcţie de aplicaţia concretă analizată. Astfel, pentru barele din oţeluri obişnuite, folosite în construcţii de maşini sau construcţii metalice, această limită se admite, în principiu, a fi cuprinsă între valorile 180 și 200.

Tensiunea critică pentru flambajul elasto-plastic

S-a constatat că dependenţa (hiperbolică) dintre scr şi l în cazul flambajului elastic modelează corect datele obţinute în practică, pentru toate tipurile de materiale. În schimb, pentru domeniul elasto-plastic nu există o exprimare matematică unică a acestei dependenţe. Modelările realizate au ca punct de pornire rezultatele experimentale (deci au un caracter empiric) şi sunt exprimate prin funcţii specifice fiecărei categorii de materiale.
De exemplu, pentru oţelurile de duritate medie, Tetmajer şi Iasinski au propus o lege de dependenţă liniară descrescătoare, sub forma:
                                                           (1.15)
în care coeficienţii a şi b (care trebuie să se măsoare în unităţi pentru tensiuni) depind de caracteristicile de rezistenţă ale oţelului considerat.
Pentru oţelurile laminate se admite că a=304 şi b=1,12  [MPa].
Pentru oţelurile aliate valorile coeficienţilor conduc la tensiuni critice mai mari (deci la o probabilitate mai mică de producere a flambajului elasto-plastic!): de exemplu, pentru un oţel aliat cu 5% Ni se iau a=461 şi b=2,26, iar l0=86. Prin urmare, barele făcute din oţeluri cu calităţi bune de rezistenţă sunt avantajoase – dacă flambajul lor este de tip elasto-plastic!
Pentru alte materiale, legea de modelare a flambajului elasto-plastic, precum şi coeficienţii incluşi în acea funcţie, se pot găsi în cărţi sau în diverse baze de date, ca şi valorile limită ale lui l care mărginesc domeniile de pe graficul tensiunii critice de flambaj.
Desigur că relaţiile de tip (1.15) nu sunt valabile pentru întregul domeniu de pe grafic aflat la stânga limitei l0: dacă pentru o bară tensiunea critică de flambaj se află deasupra limitei de curgere a materialului ei (scr³sc), atunci bara va ceda prin pierderea capacităţii de rezistenţă la compresiune, iar problema flambajului nu mai trebuie pusă.
Prin urmare, aşa cum se observă în fig. 1.6, porţiunea modelată empiric a graficului se ia în considerare numai la dreapta valorii l1 de pe abscisă (corespunzând limitei de curgere a materialului), iar între origine şi l1 tensiunea limită permisă în bară va fi egală, practic, cu sc.
Valoarea de graniţă l1 depinde şi ea de caracteristicile materialului barei, întrucât se obţine din egalarea limitei lui de curgere sc cu tensiunea critică dată de relaţia (1.15), de unde rezultă:

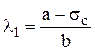
De exemplu, folosind coeficienţii recomandaţi mai sus pentru oţelurile laminate se obţin pentru limita l1 valorile 57,1 – dacă sc=240MPa, 39,3 – pentru sc=260MPa, respectiv 21,4 – dacă sc=280MPa. Pe această bază se recomandă ca l1 să fie ales, pentru oţelurile obişnuite, între 20 şi 60.

Etape de lucru la calculele de flambaj longitudinal

Pentru o bară comprimată complet cunoscută, valoarea coeficientului ei de subţirime determină modul în care se studiază probabilitatea de pierdere a stabilităţii sale elastice. Poziţia lui l pe axa absciselor din graficul tensiunii critice va arăta unde se încadrează bara, deci şi relaţiile de calcul potrivite.
Principiul pe care se fundamentează calculele de stabilitate este că funcţionarea sigură a barei se obţine dacă valoarea efectivă (cef) – dată de relaţia (1.1) – a coeficientului de siguranţă la flambaj este cel puţin egală cu valoarea impusă prin enunţul problemei sau prin tema de proiectare.
În funcţie de cerinţele problemei, etapele de lucru sunt următoarele:

A. Pentru cazurile în care se cunosc caracteristicile barei

• Se stabileşte coeficientul l, folosind relaţia (1.11).
• Dacă l<l1 – bara cedează prin compresiune, deci calculele de rezistenţă se fac ca la solicitările axiale.
• Dacă lÎ[l1; l0) – flambajul se produce în domeniul elasto-plastic; se calculează scr, cu relaţia (1.15), apoi din relaţia (1.1) se obţine forţa maximă aplicabilă barei, sau se verifică bara, din condiţia cef³cimpus.
• Dacă lÎ[l0; l2] – flambajul barei este de tip elastic; forţa critică se determină cu relaţia (1.9), apoi se face verificarea sau calculul forţei capabile (după cum se cere în problemă), ca mai sus.
• Dacă l>l2 – bara a fost incorect dimensionată şi trebuie regândită.

B. Pentru dimensionarea secţiunii transversale a barei

• Nu se cunosc dimensiunile secţiunii transversale (deşi se cunoaşte forma ei), deci coeficientul de zvelteţe nu poate fi stabilit.
• Se presupune că bara flambează în domeniul elastic (adică valoarea efectivă a lui l este situată la dreapta limitei l0).
• Din relaţia (1.9) se obţine valoarea minimă necesară a momentului de inerţie al secţiunii transversale, din care se calculează o valoare de pornire a dimensiunii secţiunii (se pre-dimensionează bara).
• Cu această valoare (rotunjită prin adaos!) se calculează coeficientul de zvelteţe lef al barei.
• Dacă lef³l0 – bara este dimensionată corect şi problema este rezolvată, adică dimensiunea stabilită mai sus este cea finală.
• Dacă lef<l0 – presupunerea iniţială nu a fost corectă, iar bara trebuie verificată, după regulile flambajului elasto-plastic. În principiu se obţine un coeficient de siguranţă insuficient, astfel încât dimensiunile secţiunii trebuie mărite treptat, refăcând calculele de verificare, până când condiţia de siguranţă este îndeplinită.

Aplicaţii

1.1. Să se calculeze forţa de compresiune pe care o poate suporta o tijă, având lungimea L şi secţiunea transversală de forma şi dimensiunile din desenul alăturat, ştiind că este încastrată şi articulată la capete şi solicitată ca în fig. 1.5.
Tija este din OL37, cu modul de elasticitate E=21×104MPa şi are parametrii dimensionali L=0,6m şi t=4mm. Coeficientul de siguranţă la flambaj se impune a fi c=4.

Rezolvare

Secţiunea transversală are două axe de simetrie, care sunt şi axele principale centrale de inerţie ale secţiunii, iar momentele principale centrale vor fi:

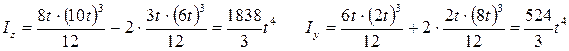
Observaţie: Pentru momentul faţă de axa z s-a făcut scăderea între momentul secţiunii brute şi al celor două dreptunghiuri “verticale” (3t×6t); faţă de axa y s-a descompus secţiunea în două dreptunghiuri “orizontale” (8t×2t) şi unul vertical – “inima” profilului – (2t×6t).

Momentul minim se obţine faţă de axa y (axa de flambaj!), iar aria secţiunii este A=44t2, încât raza minimă de inerţie este:

Din modul de rezemare rezultă lungimea de flambaj Lf=0,707×L, prin urmare coeficientul de zvelteţe pentru tija analizată este:

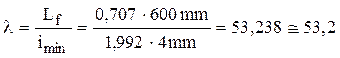
Această valoare arată că bara flambează elasto-plastic, cu tensiunea critică dată de relaţia (1.15) şi coeficienţii indicaţi. Din relaţia (1.1) rezultă formula forţei maxime pe care o poate suporta tija:

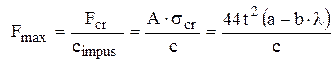
Observaţii:

• Dacă valoarea coeficientului de zvelteţe ar fi fost mai mare decât 105, atunci forţa critică s-ar fi calculat cu relaţia lui Euler.
• Se remarcă efectuarea calculelor sub formă literală, până la obţinerea relaţiei finale, singura în care (cu excepţia determinării lui l) s-au făcut înlocuiri numerice.

1.2. Să se dimensioneze o bară verticală, articulată la capete, solicitată după schema din fig. 1.1, dacă are secţiunea de formă dreptunghiulară, cu raportul laturilor h/b=2. Bara este din oţel, cu E =21×104MPa, are lungimea L=0,5m, forţa pe care trebuie să o suporte este Fef=104N, iar coeficientul de siguranţă la flambaj se va lua c=3.

Rezolvare

Coeficientul efectiv de zvelteţe nu poate fi calculat, încât se începe de la presupunerea că flambajul se produce în domeniul elastic al materialului barei (adică lef³100). Din definiţia (1.1) a coeficientului de siguranţă se scrie că Fcr = c×Fef, iar din relaţia (1.9) se obţine momentul de inerţie minim al secţiunii, sub forma:

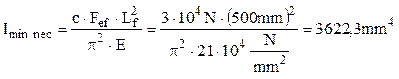
Exprimat în funcţie de dimensiunile secţiunii, cel mai mic dintre momentele de inerţie principale centrale se scrie astfel:

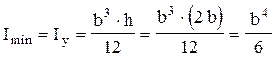
   iar din egalarea celor două valori rezultă dimensiunea preliminară a secţiunii transversale:
b = 12,142mm.
Pentru simplitate se adoptă valoarea rotunjită:
b = 15mm.
Această valoare ar putea fi dimensiunea finală a secţiunii, cu condiţia să fie îndeplinită presupunerea iniţială, în legătură cu coeficientul l.

Aria secţiunii transversale este A = 2b2, iar raza ei minimă de inerţie va fi

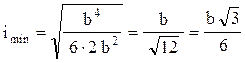
Pe aceste baze, valoarea efectivă a lui l se calculează astfel:

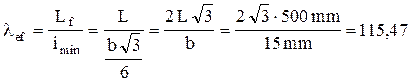
Prin urmare, coeficientul de zvelteţe real se află în domeniul flambajului elastic de pe graficul tensiunii critice (fig. 1.6). Presupunerea iniţială a fost corectă, iar dimensionarea barei este valabilă: secţiunea transversală trebuie să aibă dimensiunile b=15mm,   h=30mm.

1.3. Să se verifice stabilitatea elastică a unui stâlp din oţel, cu înălţimea de 3 metri, încastrat la partea de jos, care trebuie să susţină pe capătul liber o încărcare de 900kN şi este realizat în două variante de secţiuni, ca în figură.

Rezolvare

Pentru ambele variante constructive trebuie urmate etapele date mai sus, cu referire la problemele de verificare: se calculează aria transversală A, apoi momentul de inerţie minim al secţiunii Imin, raza de inerţie imin, respectiv coeficientul lef (ţinând seama că lungimea de flambaj este 2L=6m), care stabileşte relaţia de calcul pentru coeficientul de siguranţă la flambaj.
a) Pentru prima variantă de secţiune se obţine:

Momentul de inerţie minim se calculează faţă de axa orizontală de simetrie, în raport cu care materialul secţiunii este aşezat mai aproape:


Stâlpul flambează elasto-plastic, deci coeficientul său de siguranţă este:

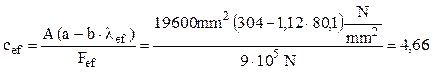
adică stâlpul nu este în pericol să-şi piardă stabilitatea elastică.

b) În cazul secţiunii inelare calculele se fac astfel:


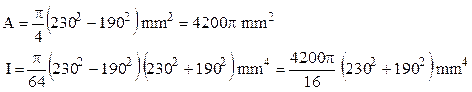
Din nou flambajul este de tip elasto-plastic, adică:

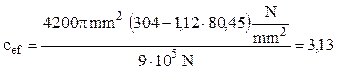
Această variantă de secţiune asigură stâlpului stabilitatea elastică cu un coeficient de siguranţă 3. Dacă se are în vedere o siguranţă mai mare, atunci trebuie redimensionată secţiunea inelară a barei.

1.4. Un stâlp vertical, din OL37, analog celui din problema anterioară, are înălţimea H = 4 metri şi trebuie să suporte pe capătul liber o forţă de 600kN, cu un coeficient de siguranţă c = 3. Se propun două variante de secţiuni transversale, ca în figura de mai jos, constante pe înălţimea stâlpului: una pătrată cu gol (raportul laturilor celor două pătrate fiind 4/5), cealaltă pătrată plină. Să se dimensioneze stâlpul în ambele variante şi să se stabilească cum se modifică, de la una la alta, volumul de material consumat pentru realizarea stâlpului.

Rezolvare

Cele două variante de secţiune au în comun valoarea momentului minim necesar de inerţie, care se calculează pornind de la presupunerea că stâlpul flambează elastic, de unde rezultă că se poate folosi formula lui Euler pentru forţa lui critică:

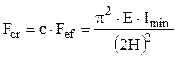
Introducând direct valorile numerice ale mărimilor se obţine:

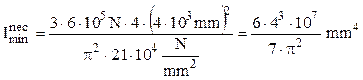
Această valoare poate fi lăsată în această formă, întrucât nu este un rezultat final, iar introducerea ei în calcule ulterioare permite efectuarea unor eventuale simplificări.
Dimensionarea iniţială a celor două tipuri de secţiuni se face egalând ultimul rezultat cu expresia literală a momentului de inerţie, în funcţie de dimensiunile precizate în figura de mai sus. Se observă că ambele variante au câte o singură valoare a momentului de inerţie, faţă de toate axele care trec prin centrele lor de greutate!

a) Pentru secţiunea tubulară expresia este:

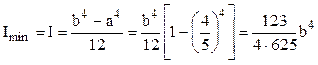
Egalând cu valoarea de mai sus se obţine b = 183,4mm, pe baza căreia se adoptă b = 184mm, de unde rezultă a= 0,8·b ≈ 147mm. Pentru ca aceste dimensiuni să fie cele finale, este nevoie să fie verificată ipoteza iniţială că stâlpul flambează în domeniul elastic.
Se urmează procedura cunoscută pentru calculul coeficientului λ:

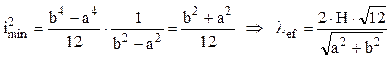
Înlocuind valorile din problemă se obţine λef = 117,67 > λ0 = 105, adică se confirmă flambajul elastic şi dimensiunile adoptate sunt corecte.

b) Pentru secţiunea pătrată fără gol mărimile caracteristice sunt:


Şi pentru acest caz se confirmă flambajul elastic al stâlpului, deci dimensiunea secţiunii a fost adoptată corect.

Pentru a calcula diferenţa dintre consumurile de material implicate de cele două variante de secţiuni se observă că, lungimea fiind aceeaşi în ambele cazuri, variaţia de volum este dată de creşterea ariei transversale în cazul secţiunii pline, în raport cu secţiunea tubulară. Prin urmare, este suficient să se facă direct raportul dintre variaţia ariei şi aria secţiunii pline: