Definirea subiectului

Construcţiile (static determinate) denumite grinzi cu zăbrele sunt formate din bare drepte prinse articulat în noduri şi alcătuind structuri (schelete) plane sau spaţiale; acestea pot înlocui cu succes plăci sau volume structurale masive, faţă de care au capacităţi similare de a prelua încărcări mecanice, dar consumuri mult mai mici de material şi implicit greutăţi mult reduse.

Exemple de construcții cu zăbrele:

Prezentarea de faţă se referă numai la construcţiile plane, la care forţele exterioare sunt aplicate exclusiv în noduri; principiile de calcul rămân valabile şi pot fi extrapolate cu relativă uşurinţă la celelalte categorii de grinzi. Trebuie observat că rezemarea articulată a barelor componente şi existenţa exclusivă a forţelor care le încarcă la capete determină ca ele să fie solicitate preponderent la întindere sau comprimare.
Într-o primă instanţă, necunoscutele dintr-o problemă de grinzi cu zăbrele sunt eforturile secţionale din bare, care se calculează prin două metode analitice de bază, descrise mai jos. Fiecare dintre ele porneşte de la secţionarea imaginară a barelor grinzii, pentru a fi puse în evidenţă eforturile necunoscute.

Principii de secţionare

Se face convenţia ca existenţa eforturilor secţionale să fie semnalată prin săgeţi, aşezate pe axa fiecărei bare secţionate, în apropierea traseului de secţionare indicat pe desenul grinzii. Sensul săgeţii se ia, în toate situaţiile, pornind de la nodul care prinde bara şi mergând către tăietura făcută, ceea ce fizic arată că bara respectivă este solicitată la întindere.
Se reaminteşte că – la studiul solicitărilor axiale – se consideră negative eforturile din barele comprimate. În acelaşi fel, eforturile din barele unei grinzi cu zăbrele vor rezulta cu semn pozitiv, pentru barele întinse, iar despre barele pentru care se obţin eforturi negative se va înţelege că sunt solicitate la comprimare.
Pentru identificarea precisă a acestor eforturi se începe prin a fi marcate, cu numere sau cu litere mari, nodurile grinzii analizate, astfel că se va nota cu Nij efortul din bara care are la capete nodurile „i” şi „j”. Desigur că ordinea în care se scriu aceşti indici nu are importanţă, dar se preferă ordonarea lor crescătoare, respectiv alfabetică.
Este interesant de remarcat că de obicei unghiurile formate între barele unei grinzi cu zăbrele au valori diverse şi ele influenţează scrierea ecuaţiilor de echilibru pe baza cărora se calculează eforturile necunoscute. Trebuie însă subliniat că mărimile propriu-zise ale acelor unghiuri nu contează, în calcule apar doar valorile unor funcţii trigonometrice ale lor, care pot fi aflate de regulă prin metode geometrice simple!

Criterii constructive

Grinzile cu zăbrele trebuie să fie static determinate şi nelabile (să nu aibă comportare de mecanism). Statica determinare se referă şi la rezemarea grinzilor, care deci trebuie făcută cu cel mult un reazem simplu şi o articulaţie. Stabilirea eforturilor din bare necesită inclusiv cunoaşterea reacţiunilor din reazeme, adică acestea trebuie calculate încă de la începutul rezolvării problemelor.
Cele două condiţii constructive ale oricărei grinzi cu zăbrele se consideră verificabile, în principiu, prin două criterii distincte, ce trebuie îndeplinite simultan:

• întrucât în fiecare nod se pot scrie două ecuaţii de echilibru, iar necunoscutele sunt eforturile din bare şi cele trei reacţiuni din reazemele grinzii, rezultă că numerele N (de noduri) şi B (de bare) ale construcţiei trebuie să verifice relaţia

2 N = B + 3                                        (2.1)

• construcţia să fie alcătuită pornind de la trei bare, prinse într-un triunghi, la care să se adauge succesiv câte două bare noi, prinse într-un nod comun (care nu exista înainte de adăugarea lor).

În plus, aceste condiţii sunt verificate şi de construcţiile obţinute prin reunirea a două grinzi cu zăbrele viabile, dacă sunt legate printr-un nod comun şi o bară ce uneşte câte un nod din fiecare grindă, sau conectate prin trei bare care nu sunt nici toate paralele şi nici toate concurente între ele (două câte două pot să fie în aceste situaţii!).

Calcule de rezistenţă

În momentul în care se cunosc toate eforturile din bare, acestea pot fi calculate din două considerente:

• rezistenţa la solicitarea axială propriu-zisă, ceea ce presupune calculul la întindere sau comprimare pentru bara cu efortul secţional cel mai mare, în valoare absolută;
• stabilitatea elastică longitudinală, verificată pentru bara cu efortul de comprimare de valoarea cea mai mare.

Ca principiu ar trebui să se facă pre-dimensionarea barelor, din solicitarea axială, urmată de verificarea la flambaj a barei cu comprimarea cea mai mare. Dacă însă aceasta este chiar bara cu solicitare maximă din grinda cu zăbrele, atunci se poate face direct dimensionarea ei la flambaj.
La finalul calculelor se adoptă dimensiunea transversală finală a barelor grinzii, în mod obişnuit cu aceeaşi valoare pentru toate barele, inclusiv pentru cele care, eventual, nu sunt deloc solicitate (au efortul axial egal cu zero!). Este important că aceste bare nu pot lipsi din construcţia analizată, iar eventuala lor deteriorare (din cauze diverse) poate provoca cedarea întregii structuri!

Calculul deplasării unui nod al grinzii cu zăbrele

La fel ca la orice structuri elastice, se poate calcula cu ce cantitate şi pe ce direcţie se deplasează un nod oarecare dintr-o grindă cu zăbrele, sub acţiunea încărcărilor ei exterioare. Teoretic, metoda de calcul se bazează pe principiul lucrului mecanic virtual (al lui d’Alembert), dar în aplicare ea se apropie foarte mult de calculul deplasărilor, la solicitările simple, folosind teorema Mohr-Maxwell.
Este necesar să fie cunoscute lungimile Li şi rigidităţile axiale EiAi ale celor N bare ale grinzii (i=1 ,..., N), dar şi eforturile Ni din bare, produse atunci când grinda suportă încărcările ei reale. Se desenează apoi o stare fictivă de solicitare, cu grinda încărcată doar cu o forţă egală cu 1 (fără dimensiuni!), aşezată (cu sens arbitrar!) în nodul de calcul P, pe direcţia Δ pe care trebuie calculată deplasarea. Se calculează eforturile ni din toate barele, după care se scrie relaţia pentru calculul deplasării cerute:
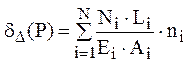                                 (2.2)
Se observă că fracţia de sub sumă are dimensiuni de lungime, iar factorul ni este adimensional (pentru că aşa este şi forţa fictivă!), deci rezultatul acestui calcul este pertinent, din acest punct de vedere. Desigur că eventualul semn pozitiv al rezultatului arată că deplasarea nodului respectiv se produce chiar în sensul ales pentru forţa fictivă de mărime unitară.
Mai este interesant de semnalat că, atunci când se calculează deplasări în mai multe noduri ale unei grinzi cu zăbrele, fracţia de sub sumă din relaţia (2.1) rămâne neschimbată (se modifică doar factorul ni, obţinut din încărcarea fictivă, care este proprie calculului respectiv)!

Dacă trebuie stabilită deplasarea totală δtot a unui nod P, atunci se aplică algoritmul de două ori, calculând pe două direcţii perpendiculare între ele, alese în mod convenabil. De obicei se folosesc verticala şi orizontala, iar relaţia finală va fi:
                            (2.3)
Folosind aceste valori se poate determina şi direcţia pe care se produce deplasarea lui P; dacă se notează cu α unghiul pe care îl face cu verticala direcţia deplasării totale, atunci se poate calcula tangenta unghiului α, folosind chiar definiţia acestei funcţii trigonometrice:
                                       (2.4)

Stabilirea eforturilor secţionale

Cele două metode analitice pentru calculul eforturilor din bare pornesc de la secţionarea imaginară a unui număr de bare, după care se scriu ecuaţii de echilibru, care conţin eforturile din barele secţionate. Principalele deosebiri între metode provin din modul de secţionare, din care rezultă tipul de ecuaţii de echilibru care pot fi scrise – doar sume ale proiecţiilor de forţe, la prima metodă, respectiv numai ecuaţii de momente, la cea de-a doua. Ilustrarea practică a aplicării acestor metode de calcul se face în aplicaţiile plasate după acest paragraf.

A. Metoda izolării nodurilor

Aceasta este cea mai simplă dintre metode şi poate fi folosită chiar şi singură, pentru găsirea eforturilor secţionale din orice fel de grindă cu zăbrele. Din denumire se poate intui că secţionările se fac, succesiv, pentru barele care se întâlnesc în jurul câte unui nod al grinzii. Eforturile având direcţii concurente, momentele lor faţă de nodul comun se echilibrează de la sine, încât singurele ecuaţii de echilibru semnificative se obţin proiectând (şi sumând) eforturile (inclusiv eventualele forţe exterioare – adică chiar şi reacţiunile – care acţionează în nodul pentru care se face calculul!) pe două direcţii reciproc perpendiculare, convenabil alese (de obicei orizontala şi verticala).
Rezultă astfel câte două ecuaţii de echilibru pentru fiecare nod, din rezolvarea cărora se găsesc pe rând eforturile din bare. Eficienţa maximă a calculelor se obţine dacă succesiunea nodurilor se alege astfel încât între barele secţionate să fie mereu cel mult două cu eforturi necunoscute (deci primul nod abordat trebuie să fie unul în care se întâlnesc doar două bare!).
Observând din nou condiţia (2.1), respectată de orice grindă cu zăbrele, se înţelege că se vor obţine 3 ecuaţii în plus faţă de numărul total de bare (pentru că reacţiunile se calculează din ecuaţii de echilibru globale ale construcţiei). Prin urmare, după ce se calculează valorile tuturor eforturilor, ultimele 3 ecuaţii de echilibru (care ar fi bine să corespundă, dacă este posibil, cu nodurile cele mai „complicate” ale grinzii!) vor putea fi folosite pentru verificarea rezultatelor obţinute până în acel moment.

B. Metoda secţiunilor arbitrare (Ritter)

De această dată traseul de secţionare (care taie în două părţi, de mărimi arbitrare, grinda cu zăbrele) poate fi ales după dorinţă, condiţia de bază fiind ca maximum trei dintre barele secţionate să conţină eforturi necunoscute. Se pot face oricâte astfel de secţiuni, iar pentru fiecare dintre ele se scriu câte trei ecuaţii de echilibru, mai precis ecuaţii de momente, calculate faţă de puncte convenabil alese situate oriunde, în planul construcţiei.
După marcarea eforturilor din bare, fiecare ecuaţie se scrie pentru numai una dintre părţile din construcţie obţinute prin secţionare, incluzând eforturile din toate barele secţionate, plus încărcările exterioare (deci și reacţiunile) care acţionează în partea aleasă. Calculul este uşurat dacă punctul faţă de care se calculează momentul este ales la intersecţia a două dintre barele cu eforturi necunoscute, efortul din cea de-a treia rămânând astfel singura necunoscută din ecuaţie.
De obicei calculul complet al grinzii prin această a doua metodă este mai laborios, în comparaţie cu prima, dar ea are avantajul că permite calculul direct al efortului din orice bară a grinzii (de exemplu pentru barele aflate la mijlocul unor construcţii cu deschideri mari), în locul paşilor „din aproape în aproape” de la metoda izolării nodurilor.

Câteva concluzii despre grinzile cu zăbrele

Panourile din grinzi cu zăbrele sunt extrem de avantajoase, ca înlocuitoare ale unor structuri masive, mult mai grele dar echivalente ca portanţă, întrucât permit realizarea unor deschideri ample (ca la podurile de cale ferată), înălţimi mari (ca la scheletul macaralelor) şi forme constructive diverse, în condiţii de economicitate maximă.
Dezavantajul lor principal este că sunt foarte sensibile la orice deteriorare a elementelor (barelor) care le compun: dacă una singură dintre barele grinzii cedează, chiar dacă este dintre cele cu eforturi secţionale nule, este foarte probabil că întreaga construcţie îşi va pierde, în mod catastrofal, capacitatea de a prelua încărcările pe care le susţine.

Aplicaţii

2.1. Să se dimensioneze barele construcţiei din figura următoare, ştiind că sunt făcute din oţel laminat cu E=21×104 şi σa=160 [MPa]. Barele orizontale şi verticale au toate aceeaşi lungime a=0,8m, cele patru forţe exterioare sunt fiecare de mărime F=3×104 N, iar coeficientul de siguranţă la stabilitatea longitudinală trebuie să fie c=3. Toate barele au secţiune pătrată, de latură t.

Rezolvare

Pe desen au fost deja numerotate cele 10 noduri ale grinzii, s-au marcat lungimile a ale barelor, ca şi valorile celor două reacţiuni din reazeme: în nodul 2 se află o articulaţie, în care însă reacţiunea orizontală nu are oponent pe grindă, adică este nulă! Pe de altă parte, construcţia este simetrică, la fel ca şi încărcarea ei, dată de cele 4 forţe F, de unde rezultă că reacţiunile verticale din reazeme trebuie să fie egale între ele, având mărimea 2F.
Grinda este static determinată şi nelabilă – criteriile de construcţie sunt îndeplinite – întrucât N=10 şi B=17, de unde rezultă 2×10=17+3, iar compunerea structurii poate fi urmărită începând de la oricare triunghi şi adăugând mereu câte două bare prinse în câte un nod comun.

a. Calculul eforturilor din bare – prin metoda izolării nodurilor
Pentru a nu încărca prea mult desenul, au fost marcate doar primele două secţionări, făcute în nodurile de pe latura din stânga a construcţiei.
Nodul 1 are ecuaţii de echilibru foarte simple, pentru care nu sunt necesare explicaţii suplimentare:

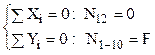
Acestea sunt eforturile din primele două bare ale grinzii.
Observaţii:

• După cum s-a arătat mai sus, calculul se începe de la un nod în care se întâlnesc doar două bare şi se continuă, pe cât posibil, cu noduri în care să apară numai câte două eforturi necunoscute! În vecinătatea nodului 1 doar nodul 10 respectă această cerinţă, deci va fi nodul următor abordat.
• Toate triunghiurile care formează construcţia (în număr de 8) sunt de tip dreptunghic isoscel, de unde rezultă că toate barele oblice sunt înclinate la 45° faţă de verticală şi de orizontală.

Nodul 10 este intersecţia a trei bare, pentru care reprezentarea simplificată şi ecuaţiile de echilibru se prezintă astfel:

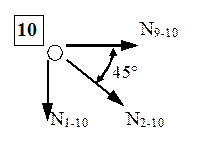
Folosind un rezultat anterior se obţine că:

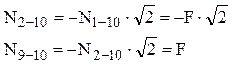
Nodul 2 conţine 4 bare (două având eforturi necunoscute), iar în ecuaţii apare şi reacţiunea verticală din acel punct:

Folosind rezultatele anterioare rezultă:

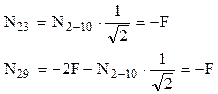
Nodul 9 conţine tot 4 bare:

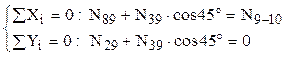
De aici rezultă:

Nodul 8 are, pe verticală, două componente, care dau: N38=-F.
Acesta este efortul din cea de-a opta bară a grinzii cu zăbrele, care închide jumătatea din stânga a construcţiei. Se poate spune că este ultimul rezultat util al acestui calcul, întrucât simetria constructivă şi de solicitare se reflectă în identitatea eforturilor din barele plasate simetric în raport cu axa globală a grinzii, care corespunde cu axa longitudinală a barei 38. O confirmare se obţine chiar din ecuaţia de echilibru scrisă pentru proiecţiile orizontale ale forţelor din nodul 8:   N78 = N89 = 0   (conform rezultatului anterior).
Pe de altă parte, rezultă că ecuaţiile de echilibru din ultimul nod semnificativ – nodul 3 – se folosesc pentru verificarea datelor deja obţinute; trebuie remarcat că echilibrul proiecţiilor pe orizontală ale forţelor din nodul 3 se verifică de la sine, întrucât barele 23 şi 39 sunt simetrice, respectiv, cu barele 34 şi 37!
Ecuaţia proiecţiilor verticale se scrie astfel:

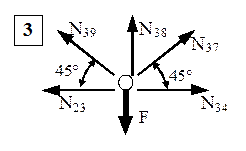
Folosind rezultatele anterioare rezultă:

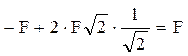
Aceasta este o identitate, care deci arată că datele obţinute sunt corecte.
Folosind legăturile de simetrie menţionate mai sus, se pot scrie valorile eforturilor secţionale din toate cele 17 bare ale grinzii, aşa cum sunt prezentate în tabelul de sinteză din pagina următoare.

b. Calculul eforturilor din bare – prin metoda secţiunilor arbitrare

Pe desen au fost reprezentate, cu liniile ondulate I-I şi II-II, două trasee de secţionare duse arbitrar prin grinda cu zăbrele considerată, singura condiţie fiind ca în barele intersectate să apară doar 3 eforturi necunoscute.

Tabel de sinteză cuprinzând eforturile calculate în problemă

Condiţia este respectată prin faptul că fiecare traseu intersectează numai câte trei bare ale grinzii, cele pentru care s-au notat pe desen simbolurile Nij ale eforturilor secţionale. Pentru simplitate, fiecare simbol a fost trecut o singură dată, deşi eforturile respective apar de ambele părţi ale secţiunilor reprezentate.
Aşa cum s-a arătat, fiecare parte de grindă obţinută prin secţionarea imaginară poate fi folosită, împreună cu eforturile secţionale figurate şi cu forţele exterioare care o încarcă, pentru scrierea a trei ecuaţii de echilibru ale momentelor, calculate în raport cu puncte arbitrare din planul desenului, alese convenabil pentru reducerea numărului de necunoscute din ecuaţie.
A. Dacă se utilizează secţionarea după traseul I-I, ecuaţiile se pot scrie în două variante:
   A1. pentru partea din dreapta a construcţiei – în care apar forţa exterioară F din nodul 5, reacţiunea 2F din nodul 4 şi eforturile necunoscute N34, N37 şi N78, rezultă

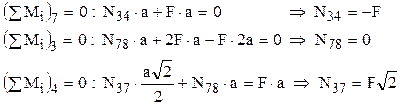
Observaţii

• Pentru fiecare termen din aceste ecuaţii, semnul momentului este dat de sensul figurat pe desen pentru acel efort, în partea din dreapta faţă de tăietura imaginară prin grindă.
• La primele două ecuaţii reperul a fost ales la intersecţia a câte două dintre barele secţionate, astfel încât fiecare ecuaţie a rămas să conţină o singură necunoscută. La ultima ecuaţie nu se mai poate evita apariţia unuia dintre eforturile calculate anterior, încât punctul de calcul a fost plasat în nodul 4 al grinzii.
• Distanţa faţă de punctul 4 a efortului N37 este notată pe desen prin segmentul 4-11 şi se obţine ca valoare, în modul cel mai simplu, scriind în două feluri aria triunghiului dreptunghic 3-4-7, ceea ce folosind segmentele de pe desen duce la

• Valorile obţinute pentru cele trei eforturi calculate mai sus coincid cu rezultatele de la metoda izolării nodurilor.

   A2. pentru partea din stânga a construcţiei – în care apar trei forţe exterioare F, reacţiunea 2F din nodul 2 şi aceleaşi eforturi necunoscute N34, N37 şi N78, rezultă

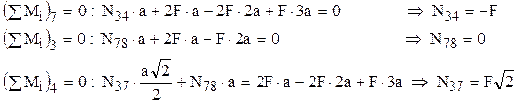
Se observă că ecuaţiile sunt ceva mai complicate faţă de cazul de mai sus, pentru că apar mai multe eforturi care produc momente, dar rezultatele sunt aceleaşi; este deci suficient să se abordeze una dintre părţile construcţiei secţionate, pentru scrierea ecuaţiilor de momente.

B. Dacă se utilizează secţionarea după traseul II-II, având o orientare oblică faţă de axele construcţiei, ecuaţiile se pot scrie tot în două variante:
   B1. pentru partea din stânga a construcţiei – în care apar forţa exterioară F din nodul 1, reacţiunea 2F din nodul 2 şi eforturile necunoscute N23, N29 şi N9-10, rezultă

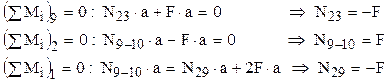
   B2. pentru partea din dreapta a construcţiei – în care apar trei forţe exterioare F, reacţiunea 2F din nodul 4 şi aceleaşi eforturi necunoscute N23, N29 şi N9-10, rezultă

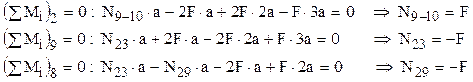
Toate observaţiile făcute anterior rămân valabile şi pentru aceste calcule, iar această metodă se poate aplica pentru aflarea tuturor eforturilor din barele grinzii, făcând numărul necesar de secţionări care să respecte condiţiile menţionate mai sus. Totuşi, se poate afirma că metoda izolării nodurilor este mai expeditivă, cel puţin pentru barele situate la extremităţile construcţiei.

c. Calculul de rezistenţă – pentru barele grinzii cu zăbrele

Din tabelul de valori se observă că solicitarea cea mai periculoasă are loc în cele patru bare oblice ale grinzii, în care efortul secţional are valoarea maximă Nmax = . Calculul se va face pentru barele 46 şi 2-10, la care acest efort are semn negativ, adică produce comprimare. Aşa cum s-a arătat, dimensionarea acestor bare se face din condiţia de stabilitatea elastică longitudinală (flambaj).
Barele sunt de secţiune pătrată cu latura t şi au lungimea L =  (care coincide cu lungimea lor de flambaj Lf).
Ipoteza de pornire este că barele flambează elastic, adică pot fi calculate cu formula lui Euler pentru forţa critică de flambaj:

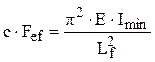
de unde se poate obţine o valoare a momentului de inerţie, respectiv a dimensiunii transversale a secţiunii barelor, sub forma:

Folosind datele numerice din problemă se obţine că:

adică tmin = 31,164mm, din care se adoptă valoarea t = 32mm.
Aceasta poate fi dimensiunea finală a barelor grinzii numai dacă se respectă ipoteza iniţială, prin valoarea coeficientului de zvelteţe efectiv al barelor. Se poate observa că pentru problema de faţă avem:

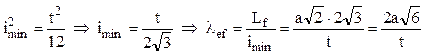
Valorile numerice ale problemei conduc la:

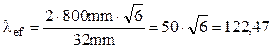
Această valoare este mai mare decât 105, care reprezintă limita la stânga, pentru oţelurile laminate obişnuite, a domeniului în care se poate folosi formula lui Euler pentru forţa critică de flambaj, deci calculele făcute au fost corecte şi grinda cu zăbrele poate fi construită din bare cu secţiunea pătrată cu latura t = 32mm.

d. Calculul deplasărilor, pe verticală – pentru nodurile 3 şi 5 ale grinzii

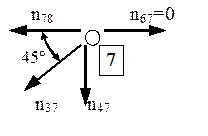
Folosind un rezultat anterior se obţine:

Desigur că toate valorile obţinute sunt valabile şi pentru barele simetrice cu cele calculate, în raport cu axa mediană verticală a construcţiei, iar aceste eforturi fictive nij sunt cuprinse şi ele în tabelul de mai sus al rezultatelor problemei de faţă.
Echilibrul eforturilor din ultimul nod semnificativ – nodul 3 – se scrie simplu, întrucât doar două bare, cele oblice, au eforturi diferite de zero. Proiecţiile lor orizontale sunt de la sine în echilibru, datorită poziţiei simetrice a acestor bare în grinda cu zăbrele considerată, iar suma proiecţiilor verticale ale forţelor se scrie astfel:

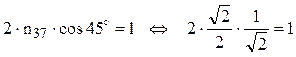
Ecuaţia este verificată, deci valorile calculate pot fi admise ca fiind corecte; folosind datele din tabelul de sinteză (coloanele 2, 3 şi 4) şi relaţia de calcul (2.2), cu observaţia că barele au aceeaşi rigiditate axială (E·A), deplasarea pe verticală a nodului 3 al grinzii se stabilește astfel (termenii dintre paranteze sunt trecuţi în ordinea din tabelul de mai sus a barelor, fiind neglijaţi cei pentru care unul dintre factori este nul!):

Observaţii

• Din tabelul cu rezultate se deduce că pentru 13 dintre cele 17 bare ale grinzii cu zăbrele considerate are valoarea zero cel puţin unul dintre eforturile secţionale (cel real Nij, respectiv cel din starea de încărcare fictivă nij), astfel încât în suma din paranteza de mai sus apar numai termenii care corespund celor 4 bare cu eforturi de valori semnificative – acestea sunt simetrice în perechi – 37 cu 39 şi 47 cu 29, de unde factorul 2 din fiecare termen din paranteză.
• Rezultatul calculelor este pozitiv, deci deplasarea nodului 3 se produce în jos (în sensul forţei unitare fictive care s-a introdus în acel nod).

Folosind datele numerice ale problemei se poate stabili şi valoarea concretă a deplasării calculate mai sus, astfel:

Calculul deplasării pe verticală a nodului 5 este ceva mai laborios, deoarece solicitarea din starea fictivă nu mai este simetrică şi trebuie stabilite eforturile (care se notează cu n*ij) din toate cele 17 bare ale grinzii.

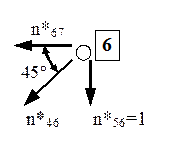
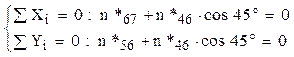
Folosind rezultatul anterior rezultă:

Nodul 4

  
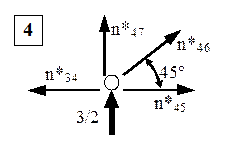
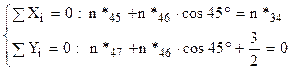
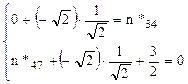
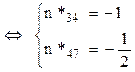
Nodul 7

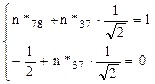
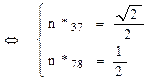
Nodul 8

Aici rezultatele se obţin imediat: n*89 = n*78 = ½,   respectiv   n*38 = 0

Nodurile 1 şi 10

Ecuaţiile din aceste noduri dau valorile: n*12 = n*1-10 = n*2-10 = n*9-10 = 0

Nodul 2

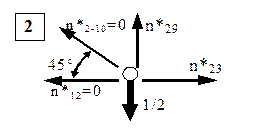
Ecuaţiile din acest nod conţin doar trei termeni de forţă, întrucât cele două componente din partea stângă a figurii sunt egale cu zero, astfel că se obţine:

n*23 = 0,   respectiv   n*29 = ½

Nodul 9

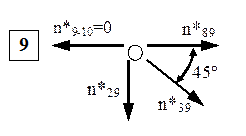
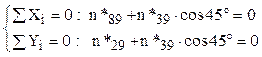
de unde rezultă
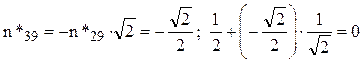Cea de-a doua ecuaţie reprezintă deja una de verificare şi se observă că este o identitate, arătând că valorile pe care le include sunt corecte.
Verificarea finală se face în ultimul nod al grinzii, singurul în care se întâlnesc cinci bare:

Nodul 3

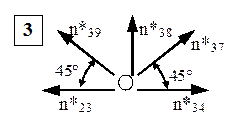
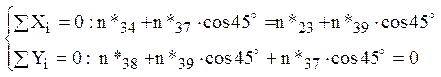
Folosind rezultatele anterioare rezultă:

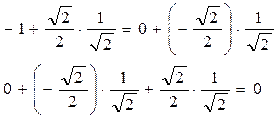
Fiecare dintre aceste relaţii este o identitate, deci se poate admite că valorile eforturilor, obţinute prin metoda izolării nodurilor, sunt corecte. Aşa cum deja s-a arătat, toate aceste valori se regăsesc în ultima coloană din tabelul de rezultate de mai sus.
Urmărind datele din tabel se observă că pentru a calcula, folosind relaţia (2.2), deplasarea pe verticală a nodului 5, termenii semnificativi (la care ambele eforturi secţionale – cel real Nij şi cel fictiv n*ij – sunt nenule) sunt daţi de numai 8 dintre barele care compun construcţia, cele numerotate cu 34, 56, 67, 29, 39, 37, 47 şi 46. Termenii respectivi apar, în această ordine, între parantezele drepte din expresia următoare:


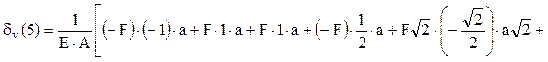
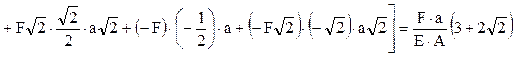
Rezultatul este şi de această dată pozitiv, arătând că nodul 5 se deplasează în jos, adică în sensul forţei unitare din starea de încărcare fictivă. Folosind acum datele numerice din problemă se poate calcula valoarea reală a acestei deplasări, astfel:

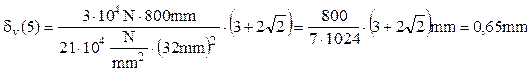
Se poate spune că valorile ambelor deplasări calculate sunt cu totul pertinente şi nu periclitează plasarea în domeniul elastic a deformaţiilor pe care le capătă barele grinzii cu zăbrele, sub acţiunea încărcărilor pe care trebuie să le suporte.
2.2. Să se calculeze valoarea maximă Fmax a forţei pe care o poate suporta construcţia din figura alăturată, cunoscând că toate barele care o compun au secţiuni circulare pline cu diametrul d = 30mm şi sunt din oţel laminat obişnuit, cu E=21×104 MPa şi σa=160MPa.
Parametrul de lungi-me este a = 400mm, iar coeficientul de stabilitate elastică longitudinală c = 2,5.
Să se determine şi valoarea deplasării pe verticală a nodului 3, atunci când încărcarea este egală cu forţa maximă de mai sus.

Rezolvare

La fel ca în cazul precedent, nodurile au fost numerotate şi reacţiunile din reazeme deja calculate şi trecute pe desen (cu sensurile lor reale), această operaţie fiind una foarte simplă. Tot simplu se face verificarea criteriilor constructive: sunt 7 bare şi 5 noduri, care îndeplinesc condiţia 2×5 = 7+3; în plus, analizând structura pornind de la triunghiul 125, se poate admite că au fost adăugate barele 24 şi 54, prinse în nodul 4, apoi barele 23 şi 43, prinse în nodul 3. Ambele criterii sunt îndeplinite, construcţia este static determinată şi nelabilă, adică i se pot aplica metodele de rezolvare descrise pentru grinzile cu zăbrele.

a. Calculul eforturilor din bare – prin metoda izolării nodurilor
Expresiile din nodul 1 sunt banale:   N12 = 0,   respectiv   N15 = 2F

Nodul 5 este intersecţia a trei bare, pentru care reprezentarea simplificată şi ecuaţiile de echilibru se prezintă astfel:

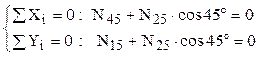
Folosind un rezultat anterior se ajunge la:

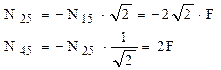
Pentru nodul 4 se scrie simplu că:   N34 = N45 = 2F,   respectiv   N24 = 0

Nodul 3 conţine doar două bare şi forţa exterioară F, aspectul particular fiind unghiul α dintre bare; după cum s-a arătat, mărimea acestui unghi nu este necesar să fie stabilită, fiind suficient să fie cunoscute valorile funcţiilor sale trigonometrice. Acestea pot fi calculate, de exemplu, din triunghiul dreptunghic 234, folosind relaţiile lor de definiţie:

Cunoscând, din trigonometrie, relaţia , rezultă:

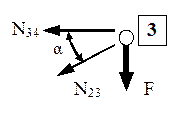
Folosind rezultatele anterioare se obţine:

Se observă că ultima valoare confirmă un rezultat de mai sus, cea de-a doua ecuaţie din nodul 3 fiind deja una suplimentară, de verificare, deoarece au fost calculate toate eforturile secţionale din bare. Tot pentru verificare se vor scrie şi ecuaţiile din nodul 2, lăsat la urmă ca fiind cel mai complex, singurul în care se întâlnesc 4 bare ale construcţiei:

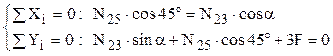
De aici rezultă:

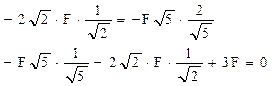
S-au obţinut două identităţi, adică se poate admite că valorile calculate mai sus ale eforturilor Nij din bare sunt corecte. Ele sunt cuprinse în tabelul care urmează, împreună cu eforturile nij care corespund stării fictive de încărcare pentru calculul deplasării pe verticală în nodul unde acţionează forţa F.

b. Calculul de rezistenţă

Valorile eforturilor secţionale arată că solicitarea periculoasă pentru barele grinzii este de comprimare şi are loc în bara oblică 25, pentru care avem:
Nmax = N25 = -   şi   Lf = .
De această dată construcţia barelor este cunoscută – ele au secţiuni circulare pline, cu diametrul d = 30mm şi parametrul a = 400mm, deci poate fi stabilit modul în care bara 25 tinde să-şi piardă stabilitatea elastică. Cunoscând că raza de inerţie a secţiunilor circulare este un sfert din diametrul lor, rezultă:

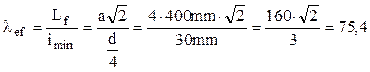
Această valoare a coeficentului de zvelteţe arată că bara tinde să flambeze în domeniul elasto-plastic, pentru care coeficentul de siguranţă se scrie:

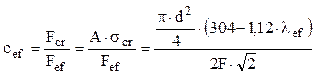
De aici rezultă forţa maximă care poate fi preluată de grinda cu zăbrele:

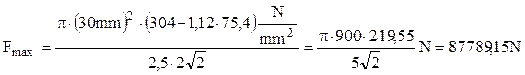
Pentru simplificarea calculelor finale, adoptăm   Fmax = 87700N.

c. Calculul deplasării, pe verticală, a nodului 3 al grinzii cu zăbrele

Pentru situaţia de faţă, în care calculul trebuie făcut chiar în punctul şi pe direcţia în care acţionează singura forţă exterioară F de pe grindă, starea fictivă este perfect echivalentă stării reale de solicitare, în care însă trebuie luată valoarea F = 1 (număr fără dimensiuni).
În aceste condiţii, eforturile secţionale fictive nij au valorile incluse în tabelul de rezultate de mai sus, în care sunt trecute (în funcţie de parametrul a) şi lungimile tuturor barelor grinzii cu zăbrele. Folosind relaţia (2.2) şi reamintind că barele au aceeaşi rigiditate axială EA, deplasarea cerută se calculează astfel:


Aceste calcule arată că nodul 3 se deplasează (în jos!) cu 0,236mm.