|
Starea de tensiuni în jurul unui punct
Atunci când un corp solid oarecare se află sub acţiunea unui sistem arbitrar de încărcări mecanice, legăturile fizice dintre particulele de material care îl alcătuiesc sunt puse la încercare, cu o intensitate (numită tensiune mecanică) ce depinde de tipul şi de nivelul solicitărilor care se produc, dar şi de poziţia, în volumul corpului, a punctului în care se face analiza, precum şi de direcţia pe care se cuantifică tensionarea materialului.
S-a arătat anterior că tensiunea se notează, în mod generic, cu litera p, că se măsoară în unităţi de presiune (1MPa = 1N/mm2) şi că se studiază de obicei prin componentele sale – normală (σ), respectiv tangenţială (τ) – pe planul pe care tensiunea respectivă acţionează.
Se înţelege că valorile acestei mărimi rezultă diferite, atunci când se măsoară (sau se calculează) pe direcţii diferite, în jurul punctului în care se face analiza. Ansamblul acestor valori formează starea de tensiuni din acel punct al corpului studiat.
Observaţie: Procedând în mod analog, dar cu referire la schimbările de poziţii şi de dimensiuni ale segmentelor de particule din jurul unui punct, din volumul unui corp solicitat mecanic, se defineşte starea de deformaţii specifice din acel punct. Componentele pe care se bazează studiul sunt alungirile specifice (ε) şi lunecările specifice (γ), iar analiza prezintă multe similitudini cu ceea ce se va prezenta mai jos pentru stările de tensiuni.
Tensorul tensiunilor
Se imaginează trei plane, reciproc perpendiculare (ce vor determina axele de coordonate folosite în cursul analizei), care se intersectează în punctul arbitrar P, ales pentru studiu. Pe baza acestor plane se construieşte un paralelipiped drept, având laturi care se consideră de dimensiuni infinit mici, adică fiind reductibil, la limită, la însuşi punctul P.
Admiţând că solicitările exterioare duc la apariţia unor componente de tensiuni pe orice direcţie, în jurul lui P, adică starea de tensiuni din acel punct este spaţială (tri-dimensională), rezultă că pe fiecare faţă a paralelipi-pedului pot fi identificate câte trei componente ale tensiunilor – una de tip normal şi două de tip tangenţial, fiecare în parte paralelă cu câte una dintre axele de coordonate (respectiv cu muchiile paralelipipedului), ca în figura 3.1.a de mai jos.
|
Aşa cum se arată în figură, componentele de tip tangenţial se notează cu doi indici, primul pentru axa care este perpendiculară pe planul acelor tensiuni, al doilea pentru axa cu care componenta respectivă este paralelă. Pe această bază, tensiunile normale ar trebui scrise cu câte doi indici identici, astfel că s-a convenit ca indicele să fie scris o singură dată.
Starea de tensiuni din punctul P se consideră cunoscută în totalitate dacă sunt cunoscute cele 9 componente din fig. 3.1.a; valorile acestora se prezintă de obicei sub formă de matrice, notaţie denumită tensorul tensiunilor din P:
(3.1)
Observaţie: Noţiunea de tensor (având 9 componente) este cunoscută din matematică şi fizică, unde este definită ca generalizare a noţiunii de vector (caracterizat prin trei componente – proiecţiile pe axele de coordonate).
Desigur că, în funcţie de specificul unei stări concrete de tensiuni, o parte dintre cele nouă componente de tensiuni pot avea valoarea zero; în aceeaşi ordine de idei, dacă starea de tensiuni este plană, având adică valori nenule pentru doar patru componente, paralele cu două dintre axele de coordonate (ca în fig. 3.1.b), tensorul tensiunilor se scrie simplu:
(3.2)
Observaţie: Figura 3.1 conţine, pentru starea spaţială de tensiuni, doar componentele de pe feţele vizibile ale volumului elementar considerat; acelor componente însă le corespund, în mod evident, perechi ale lor care acţionează pe feţele nevizibile, aşa cum se poate vedea în reprezentarea alăturată a stării plane de tensiuni (fig. 3.1.b).
Studiul stărilor plane de tensiuni
Pentru a se înţelege cum apare o astfel de stare de solicitare, se poate imagina o placă de grosime constantă, dintr-un material oarecare, în al cărei plan median acţionează un sistem de forţe coplanare, aflate în echilibru: efectele solicitării sunt identice în toate planele paralele cu cel median, iar tensiunile ce apar în material sunt cuprinse chiar în planul în care acţionează forţele exterioare.
Trebuie precizat că starea de deformaţii specifice implicată de această solicitare nu este, în mod necesar, tot plană! În schimb, dacă placa este plasată, de exemplu, între doi pereţi rigizi, paraleli cu planul ei median, atunci este împiedicată producerea deformaţiilor pe direcţii perpendiculare pe acest plan şi starea de deformaţii specifice este plană!
O primă problemă importantă în studiul stărilor plane de tensiuni este calculul componentelor σα şi τα ale tensiunii care acţionează pe un plan definit arbitrar, în jurul punctului oarecare P în care se face analiza, atunci când sunt cunoscute componentele de pe planele care au ca normale axele de coordonate, ca în figura 3.1.b.
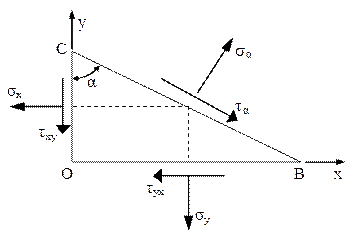 Fig. 3.2 |
Volumul elementar se alege de forma unei prisme cu bază triunghiulară (fig. 3.2), iar pe feţele ei se plasează cele 6 componente de tensiuni. Aria feţei înclinate a prismei se notează cu dA, astfel că faţa orizontală (ce conţine pe OB) are aria (dA·sinα), iar faţa verticală - (dA·cosα).
Admiţând că elementul de volum se află în echilibru sub acţiunea efectelor de tip forţă produse de aceste componente ale tensiunilor, proiecţiile acestor forţe pe direcţiile lui σα şi τα se scriu astfel:
Toţi termenii acestor ecuaţii de echilibru au rezultat din înmulţirea componentelor de tensiuni cu ariile feţelor pe care ele acţionează asupra volumului elementar şi apoi din proiectarea acestor mărimi fizice (de tip forţă) pe direcţiile componentelor de pe faţa înclinată.
Situaţia de încărcare din figura 3.2 respectă principiul dualităţii tensiunilor tangenţiale, de unde rezultă că τxy = τyx şi ţinând seama că ambele ecuaţii pot fi împărţite prin dA – cantitate strict pozitivă, se obţin următoarele expresii pentru componentele de tensiuni de pe faţa înclinată a elementului de volum considerat:
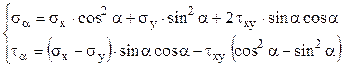(3.3)
Aceste relaţii pot fi scrise şi în funcţie de unghiul (2α), astfel:
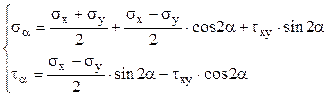(3.4)
Pentru a găsi valorile extreme (principale) ale tensiunilor normale din jurul punctului P ales pentru studiu, se derivează prima dintre aceste relaţii, în raport cu argumentul (2α):
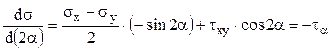
De aici rezultă, pe de o parte, că tensiunile tangenţiale trebuie să aibă valoarea zero (pentru ca derivata de mai sus să fie nulă!) pe direcţiile principale ale tensiunilor normale. Pe de altă parte se obţine o condiţie pe care trebuie să o îndeplinească aceste direcţii principale, adică:
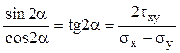(3.5)
Se observă că soluţia acestei ecuaţii trigonometrice, reprezentând unghiul făcut, în raport cu axa (y) ataşată elementului de volum studiat, de direcţia tensiunilor normale principale, se scrie:
adică se obţin două direcţii principale, perpendiculare între ele!
Valorile tensiunilor normale principale pot fi obţinute, de exemplu, scriind (cu formule din trigonometrie) pe sin2α şi cos2α în funcţie de tg2α şi apoi de componentele de tensiuni, pe baza relaţiei (3.5), după care aceste rezultate se introduc în prima dintre expresiile (3.4). Formulele finale se scriu, în formă sintetică, astfel:
(3.6)
Pe această bază se calculează, prin urmare, valorile extreme – cea mai mare (σ1), respectiv cea mai mică (σ2) (atenţie: în sensul poziţiei lor pe axa numerelor reale!) ale tensiunilor normale care se produc pe volumul elementar ales pentru studiu; se reaminteşte că s-a pornit de la cunoaşterea componentelor de tensiuni având direcţia unor axe de coordonate arbitrare, ataşate elementului de volum.
Observaţie: Adunând între ele cele două variante ale expresiei (3.6) se obţine că σ1 + σ2 = σx + σy = ct, adică suma valorilor tensiunilor normale de pe oricare două direcţii perpendiculare între ele este un acelaşi număr, care reprezintă un invariant al oricărei stări plane de tensiuni!
Dacă se urmează pas cu pas procedura de mai sus, cu referire la tensiunile tangenţiale de pe elementul de volum analizat, se obţine că direcţiile lor principale îndeplinesc condiţia:
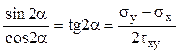(3.7)
Ultima fracţie este inversă celei din relaţia (3.5), ceea ce conduce la soluţiile α3, 4 care au legătură cu direcţiile principale ale tensiunilor normale, adică cu unghiurile α1, 2 obţinute mai sus, mai precis: α3, 4 = α1, 2 + 45° .
Prin urmare, valorile extreme ale tensiunilor tangenţiale se obţin tot pe două direcţii perpendiculare între ele şi care sunt bisectoare pentru direcţiile principale ale tensiunilor normale din aceeaşi stare plană de tensiuni!
Procedând ca mai sus se pot stabili şi valorile concrete ale tensiunilor tangenţiale principale, care rezultă sub forma:
(3.8)
Observaţii
(3.9)
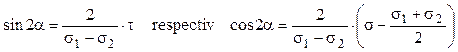
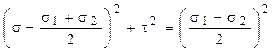(3.10)
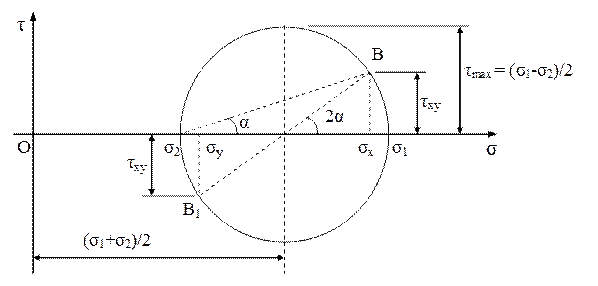 Fig. 3.3 |
Se observă că, în sistemul de axe (σ-τ), aceasta este ecuaţia unui cerc, având raza egală cu 
şi centrul pe axa σ, la poziţia 
:
Acest mod de reprezentare grafică a unei stări plane de tensiuni este numit cercul lui Mohr, despre care se observă deja pe desen (fig. 3.3) că oferă în mod direct informaţii importante cu privire la parametrii stării respective, începând cu mărimile valorilor principale ale tensiunilor σ şi τ.
Pe de altă parte, coordonatele oricărui punct B de pe cerc, notate cu σx şi τxy, reprezintă valorile componentelor de tensiuni care acţionează pe o suprafaţă înclinată cu unghiul α faţă de axa y ataşată elementului de volum ales la începutul studiului, după cum coordonatele σy şi (-τxy) ale punctului B1, aşezat tot pe cerc, diametral opus lui B, reprezintă componentele de pe o suprafaţă perpendiculară pe cea desemnată de B.
Prin urmare, dacă se cunosc valorile tensiunilor normale principale ale stării de tensiuni, atunci ele se plasează în sistemul de axe şi se figurează cercul, după care tensiunile pe suprafaţa înclinată la unghiul arbitrar α şi pe cea normală la aceasta vor fi reprezentate prin punctele B, respectiv B1, aflate la capetele diametrului înclinat la unghiul 2α faţă de axa orizontală σ.
Tot prin această metodă grafică se poate rezolva şi problema inversă în care, cunoscând componentele de tensiuni σx, σy şi τxy de pe două plane perpendiculare între ele duse prin punctul analizat, trebuie aflate tensiunile principale şi direcţiile lor: se plasează pe desen punctele B şi B1, cu acest segment luat ca diametru se trasează cercul, cu centrul în punctul lui de intersecţie cu axa σ. Cercul taie axa în dreptul mărimilor σ1 şi σ2, iar prima direcţie principală face unghiul α (jumătate din înclinarea segmentului B1B faţă de axa σ) cu suprafaţa simbolizată de punctul B.
Aplicaţii
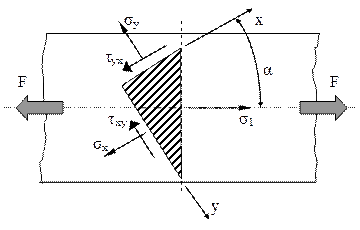 Fig. 3.4 |
3.1. Volumul elementar din figura alăturată se decupează imaginar dintr-o bară supusă la tracţiune cu forţele F. Dacă se cunosc σx = 50, σy = 30 [MPa] şi aria transversală a barei A = 300mm2, să se afle valorile mărimilor următoare:
a. tensiunea tangenţială τxy;
b. încărcarea exterioară F;
c. tensiunea principală τmax;
d. înclinarea α a elementului de volum considerat, faţă de axa barei.
Rezolvare
Se porneşte de la observaţia că tensiunea normală principală σ1 va avea chiar direcţia forţelor F, în vreme ce σ2 trebuie să fie zero!
Folosind relaţia (3.6) pentru calculul tensiunilor normale principale, în care se înlocuiesc direct cele două componente de tensiuni date în enunţ (şi măsurate în MPa), se obţine:
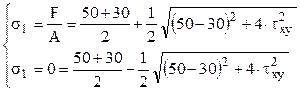
Cea de-a doua egalitate permite aflarea componetei de tensiune τxy:
Pentru a se stabili mărimea încărcărilor exterioare F, se introduce valoarea tocmai găsită în prima egalitate de mai sus, de unde rezultă că:
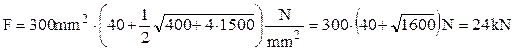
Tot folosind relaţia (3.9) şi sistemul de egalităţi de mai sus, se calculează tensiunea tangenţială principală:
În fine, din relaţia (3.5) se calculează unghiul α dintre axa x, ataşată elementului de volum ales şi direcţia tensiunii principale σ1, astfel:
3.2. Pe un volum elementar de formă prismatică, similar celui de mai sus şi decupat imaginar dintr-un corp solid încărcat mecanic într-un mod oarecare, se cunosc componentele de tensiuni: σx = 120, σy = 40 şi τxy = 50 [MPa]. Să se stabilească valorile tensiunilor principale, precum şi direcţiile acestora.
Rezolvare
Relaţia (3.6) permite calculul tensiunilor normale principale:
Se obţin deci valorile σ1 = 144, respectiv σ2 = 16 [MPa].
Din relaţia (3.5) rezultă:
Acesta este unghiul, măsurat în sens antiorar, făcut de direcţia tensiunii principale σ1 cu axa x ataşată elementului de volum considerat.
Tensiunile tangenţiale principale au, în modul, valoarea:
Direcţiile acestora se obţin rotind cu 45°, în oricare dintre sensuri, direcţiile principale ale tensiunilor normale. Se reaminteşte că cele două direcţii principale sunt perpendiculare una pe alta, pentru ambele categorii de tensiuni.
Cazuri particulare de stări plane de tensiuni
Pentru multe situaţii practice de solicitări mecanice, stările tipice de tensiuni sunt de tip plan, astfel că este util să fie discutate câteva cazuri mai des întâlnite.
A. Starea liniară de tensiuni – prezentă la tracţiunea sau compresiunea uniaxială, respectiv la încovoierea pură; luând axa x pe direcţia solicitării, se obţine că σy = 0 şi τxy = 0.
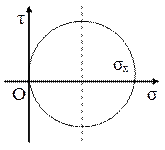 Fig. 3.5 |
Rezultă imediat că tg2α = 0, prima direcţie principală fiind dirijată chiar pe axa x, iar expresiile tensiunilor principale sunt:
Aceste proprietăţi sunt observabile şi pe cercul lui Mohr trasat alăturat pentru această stare de tensiuni.
B. Starea de forfecare pură – întâlnită şi la răsucirea tuburilor cu pereţi relativ subţiri; dacă pentru un volum elementar din pereţii unui astfel de tub se alege axa x paralelă cu axa longitudinală a tubului, atunci componentele normale de pe feţele elementului vor fi nule: σx = σy = 0.
 Fig. 3.6 |
Pentru acest caz se obţine tg2α = ∞, adică 2α = 90°, respectiv α = 45°. Tensiunile normale principale sunt înclinate la 45°, respectiv 135° în raport cu axa x ataşată volumului elementar, iar valorile lor sunt:
Cele două tensiuni principale sunt de întindere, respectiv de comprimare, de valori egale cu tensiunea tangenţială care produce forfecarea pură şi care va reprezenta chiar raza cercului Mohr pentru această solicitare (fig. 3.6).
C. Starea de încovoiere cu forfecare – este starea de tensiuni caracteristică pentru încovoierea simplă, adică pentru cele mai multe dintre grinzile concrete. Dacă elementul de volum se alege cu axa x în lungul axei unei astfel de grinzi, atunci componenta σx va fi tensiunea de încovoiere din fibra respectivă a barei, calculată din relaţia lui Navier, tensiunea tangenţială τxy se va calcula folosind relaţia lui Juravski, iar componenta σy, perpendiculară pe axa barei, va fi nulă.
Prin urmare, direcţiile şi tensiunile principale date de relaţiile (3.5) şi (3.6) se vor obţine sub forma:
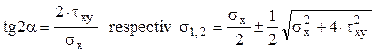
Este important de observat că valorile tensiunilor principale se modifică mereu, atunci când elementul de volum analizat se mută de la o fibră la alta a grinzii, pe o aceeaşi direcţie, perpendiculară pe axa longitudinală a barei (respectiv pe axa ei de încovoiere, notată de obicei cu z), adică pe direcţia axei iniţiale y. Se schimbă în mod continuu şi direcţia axelor principale, care practic se rotesc cu 90°, aşa cum se va arăta în continuare.
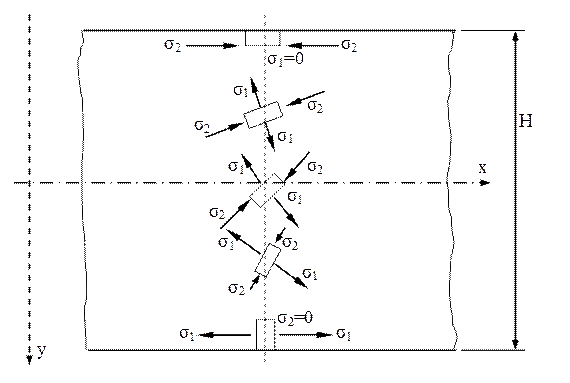 Fig. 3.7 |
Folosind noţiuni elementare din studiul solicitărilor simple şi admiţând o grindă cu secţiune simetrică faţă de axa de îndoire (încât evoluţia tensiunilor pe secţiune să fie cea descrisă mai jos) şi cu un efort de încovoiere de sens pozitiv, în secţiunea transversală aleasă pentru studiu, adică producând întindere în fibrele longitudinale aflate în grindă sub planul neutru, rezultă următoarele:
Starea generalizată (spaţială) de tensiuni
Pentru o astfel de stare de solicitare tensorul tensiunilor – scris sub forma (3.1) – are 9 componente, reprezentate în fig. 3.1.a pe feţele unui element de volum arbitrar, de formă prismatică, construit în punctul oarecare P din corpul solid ales a fi studiat. Cunoscând aceste componente se pot stabili, aşa cum se va arăta în continuare, componentele de tensiuni de pe orice plan dus prin punctul considerat.
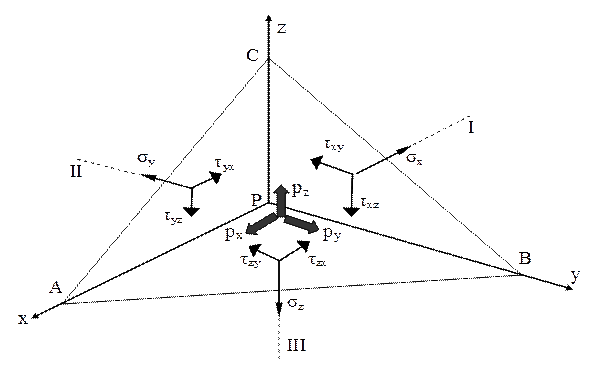 Fig. 3.8 |
Deducerea relaţiilor de calcul se bazează pe acelaşi element de volum prismatic, la care muchiile care se intersectează în punctul P coincid cu axele de coordonate. Se imaginează că această prismă este secţionată cu un plan, de înclinare oarecare (fig. 3.8), ce întâlneşte axele x, y, z în punctele A, B, respectiv C. Se formează astfel un tetraedru, la care planele care au ca punct comun pe P sunt două câte două reciproc perpendiculare, iar baza opusă lui P este triunghiul oarecare ABC, a cărui arie se notează cu dA.
Înclinarea acestui plan se arată prin funcţia „cosinus” a unghiurilor făcute de normala la plan cu axele x, y, z („cosinusuri directoare” ale planului) şi care se notează prin literele l, m, respectiv n. Este util de reamintit că aceste trei mărimi se află în relaţia l2 + m2 + n2 = 1.
Cu ajutorul lor se pot exprima şi mărimile ariilor celorlalte trei feţe ale tetraedrului: astfel, pentru PAB se observă că are ca normală axa z, având înclinarea n faţă de normala la planul ABC. Rezultă APAB = n·dA şi în mod analog se obţine că: APAC = m·dA, respectiv APBC = l·da.
Feţele tetraedrului elementar au fost considerate transparente, astfel încât să fie vizibile cele 9 componente ale tensorului tensiunilor, plasate pe feţele pe care acţionează (cele care se intersectează în P), cu respectarea notaţiilor convenite anterior. Pe suprafaţa înclinată ABC apare o tensiune p, de mărime şi direcţie necunoscute, figurată (în centrul de greutate!) prin componentele ei px, py şi pz de pe direcţiile axelor de coordonate.
Efectele de tip forţă ale componentelor de tensiuni se obţin ca produs între mărimile lor şi ariile suprafeţelor pe care acţionează, astfel că se pot scrie ecuaţii de echilibru pentru proiecţiile acestor forţe pe direcţiile notate pe desen cu I, II, respectiv III (practic pe fiecare dintre axe dau proiecţii numai componentele paralele cu axa):
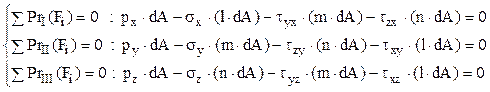
Se observă că fiecare dintre aceste ecuaţii poate fi împărţită prin cantitatea dA, care este strict pozitivă, iar sistemul care se obţine cuprinde ecuaţiile lui Cauchy (cel care le-a scris pentru prima dată, în anul 1823) pentru calculul componentelor tensiunii de pe faţa înclinată a tetraedrului elementar:
(3.11)
Aceste expresii pot fi scrise compact, observând că în membrul drept apare tensorul Tσ al tensiunilor şi matricea coloană a cosinuşilor directori:
(3.12)
Este util să se scrie şi ecuaţiile de echilibru pentru momentele date de forţele produse de componentele de tensiuni din fig. 3.8; dacă se admite că toate componentele acţionează în centrele de greutate ale feţelor respective ale tetraedrului elementar, se observă că sumele de momente calculate în raport cu axele I, II, respectiv III rămân cu câte numai doi termeni semnificativi, aşa cum se exemplifică, cu raportare la axa I (care este paralelă cu axa x şi trece prin centrele de greutate ale feţelor ABC şi PBC):
De această dată ariile feţelor au fost exprimate ca semi-produs al catetelor, iar lungimea din afara parantezelor reprezintă distanţa de la axa I până la feţele pe care acţionează tensiunile tangenţiale respective. Se observă că, după simplificări, se obţine că τyz = τzy, ceea ce exprimă tocmai principiul dualităţii tensiunilor tangenţiale pentru care se face, pe această cale, o nouă verificare. Procedând analog, cu raportare la axele II, respectiv III se obţin şi celelalte două egalităţi: τxz = τzx şi τxy = τyx.
Consecinţa importantă a acestor relaţii este că tensorul tensiunilor Tσ dat de expresia (3.1) este întotdeauna simetric faţă de diagonala lui principală, atât pentru stările spaţiale, cât şi pentru stările plane de tensiuni, deci numărul componentelor independente de tensiuni este de 6, în loc de 9, respectiv 3, în loc de 4!
Revenind la tensiunea p care acţionează pe faţa ABC, de înclinare arbitrară (dar cunoscută), mărimea ei poate fi stabilită uşor, atunci când se cunosc proiecţiile ei de pe direcţiile axelor de coordonate, date de relaţiile (3.11) şi (3.12) de mai sus, întrucât:
(3.13)
Direcţia acestei tensiuni este dată de diagonala paralelipipedului având ca laturi cele trei proiecţii din relaţia (3.13). Întrucât se preferă a se lucra cu alte componente ale tensiunii p, proiecţiile ei σ – pe normala la planul ABC, respectiv τ – pe planul ABC, se foloseşte o metodă relativ simplă pentru a obţine şi mărimile acestora.
Astfel, se calculează mai întâi valoarea σ, sumând proiecţiile, pe direcţia normalei la planul ABC, ale efectelor de tip forţă produse de componentele de pe axele de coordonate ale tensiunii p:
În acest mod se obţin relaţiile finale cu care se calculează σ şi τ, astfel:
(3.14)
Tensiuni principale
Prin analogie cu stările plane de tensiuni, dacă pe o suprafaţă cu orientare arbitrară, dusă prin punctul P, ales pentru studiu, componenta tangenţială τ este nulă, iar tensiunea p se confundă cu componenta ei σ, se spune că acea suprafaţă este un plan principal pentru respectiva stare spaţială de tensiuni, iar proiecţiile pe axele de coordonate ale lui p se scriu:
Ecuaţiile (3.11) scrise pentru această situaţie conduc la sistemul:
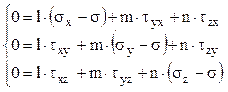(3.15)
Acestor ecuaţii li se adaugă relaţia l2 + m2 + n2 = 1 şi se obţin 4 ecuaţii în necunoscutele l, m, n şi σ, adică valoarea tensiunii normale principale şi parametrii direcţiei principale care îi corespunde. Se reaminteşte că sistemul omogen (3.15) va avea şi alte soluţii decât cea banală (în care l=m=n=0) dacă şi numai dacă determinantul sistemului este egal cu zero:
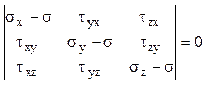(3.16)
Dezvoltarea acestui determinant duce la o ecuaţie de gradul 3, în necunoscuta σ, reprezentând ecuaţia seculară a stării de tensiuni studiate:
(3.17)
Coeficienţii din această ecuaţie sunt invarianţi, pentru o stare dată de tensiuni, în sensul că au aceleaşi valori, indiferent de alegerea volumului elementar pe care se definesc parametrii tensorului tensiunilor, inclusiv în cazul în care direcţiile x, y, z coincid cu direcţiile principale şi tensorul Tσ are doar trei termeni nenuli – cei de pe diagonala principală (valorile tensiunilor normale principale din acel punct).
Făcând calculele în relaţia (3.16) se obţine următoarele expresii ale celor trei invarianţi:
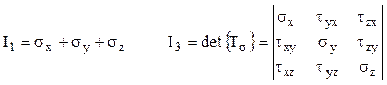(3.18)
După ce se calculează aceşti coeficienţi, folosind valorile, deja cunoscute, ale termenilor din tensorul tensiunilor, se completează ecuaţia seculară (3.17), care în condiţiile date va avea trei rădăcini reale – valorile tensiunilor normale principale din punctul P, care se aşează pe axa numerelor reale şi se numerotează în sens descrescător: σ1 > σ2 > σ3.
Direcţiile pe care sunt dirijate tensiunile principale se stabilesc introducând, succesiv, valorile acestora în ecuaţiile sistemului (3.15), din care se obţin cosinusurile directoare l, m, n ale fiecărei direcţii principale a tensiunilor. La fel ca la starea plană, se obţin 3 direcţii perpendiculare între ele şi, aşezând pe fiecare direcţie tensiunea principală care îi corespunde, se poate defini locul geometric al vârfurilor tuturor tensiunilor din jurul punctului P, care se numeşte elipsoidul tensiunilor din acel punct.
În legătură cu tensiunile tangenţiale, se demonstrează că valorile lor extreme au loc în plane ale căror normale fac unghiuri de 45° cu câte două direcţii principale ale tensiunilor normale şi sunt paralele cu cea de-a treia, iar valorile principale propriu-zise se calculează folosind relaţii similare cu cele din starea plană:
(3.19)
|
Parametrii principali ai stărilor spaţiale de tensiuni pot fi reprezentaţi şi grafic (fig. 3.9), la fel ca la starea plană, dar folosind trei cercuri Mohr – unul mare, definit de valorile principale σ1 şi σ3 şi două mai mici, care sunt înglobate de către primul cerc. Se observă că regulile după care sunt trasate cercurile sunt aceleaşi ca la starea plană, în schimb „vârfurile” tensiunilor (ale căror „începuturi” se află în originea axelor de coordonate) nu ocupă întreg spaţiul din interiorul cercului mare, ci doar pe cel haşurat, aflat în afara cercurilor mici.
Trebuie semnalat, atât pe baza calculelor cât şi din reprezentarea grafică de mai sus, faptul că valoarea τ13 este cea mai mare, în modul, dintre tensiunile tangenţiale principale, adică este cea mai mare tensiune tangenţială care se produce în jurul punctului P. Ea acţionează pe plane paralele cu tensiunea normală principală σ2 şi este înclinată, sub unghiuri de 45°, în raport cu direcţiile celorlalte două tensiuni principale, σ1 şi σ3.
Tot de pe grafic se observă că tensiunile normale din jurul punctului P au valoarea maximă σ1 şi cea minimă σ3, iar despre σ2 se mai spune că este tensiunea „mini-max”, adică este cea mai mică valoare în planul pe care îl formează cu σ1, dar cea mai mare în planul făcut cu σ3.
Tensiuni octaedrice
Acesta este un subiect legat în mod direct de cel al tensiunilor normale principale, pentru orice stare spaţială – este vorba despre tensiunile care acţionează pe planele egal înclinate faţă de direcţiile principale, numite plane octaedrice, având o relaţie particulară între cosinuşii directori:
Dacă se construieşte un tetraedru elementar, ca în figura 3.8, folosind planele principale ale tensiunilor (pe care acţionează, ca normale, tensiunile principale σi, iar tensiunile tangenţiale sunt nule), atunci mărimea totală a tensiunii octaedrice se calculează astfel:
(3.20)
Folosind relaţiile (3.14) se calculează şi componentele ei:
(3.21)
(3.22)
Aceste mărimi sunt importante, sub diverse aspecte, în teoria elasticităţii şi a plasticităţii, iar despre componenta σoct este interesant de remarcat faptul că reprezintă media aritmetică a tensiunilor normale principale din punctul ales pentru a se analiza starea de solicitare.
Concluzii privind studiul stărilor de tensiuni
Observaţie: Toate aspectele discutate până aici, cu privire la analiza stărilor de tensiuni, sunt valabile inclusiv pentru domeniul în care materialele se deformează plastic (adică permanent), întrucât nu s-au folosit şi nu au fost necesare ipoteze privind comportarea lor elastică şi nu s-au făcut referiri la constantele elastice ale materialelor. Ceea ce urmează în acest capitol, în schimb, se bazează pe elasticitatea materialelor şi poate fi valabil în domeniul plastic numai prin excepţie, aşa cum se va preciza în text.
Legea lui Hooke pentru stările spaţiale de tensiuni
În cadrul discuţiilor pregătitoare pentru studiul solicitărilor simple, a fost prezentată (pentru cazul solicitărilor unidirecţionale) legea fundamentală a elasticităţii, enunţată prima oară de fizicianul englez Robert Hooke (1678) şi referitoare la proporţionalitatea dintre încărcările aplicate barelor şi efectele (deformările) produse asupra lor. S-a precizat că această lege se respectă (desigur, cu o anumită aproximaţie, pentru multe dintre materialele concrete), doar în măsura în care deformaţiile sunt reversibile, adică dispar atunci când încetează acţiunea încărcărilor exterioare, proprietate fizică numită elasticitate.
În cazul stărilor de tensiuni multi-axiale deformaţiile care se produc apar, în volumul corpului solid, pe mai multe direcţii simultan, iar mărimile lor nu sunt independente. Pentru materialele neomogene şi anizotrope, aceste dependenţe sunt complexe, datorită faptului că proprietăţile lor mecanice şi elastice au valori diferite, atunci când sunt stabilite pe direcţii diferite din volumul de material analizat. O astfel de situaţie nu face obiectul prezentării de faţă, astfel încât discuţia se va restrânge la materialele omogene şi izotrope. Multe dintre materialele reale se încadrează în aceste categorii, inclusiv în virtutea uneia dintre ipotezele de bază ale rezistenţei materialelor, care enunţă tocmai acest lucru.
Se porneşte deci de la ipoteza că materialul se va comporta într-un acelaşi fel, indiferent de direcţia pe care este solicitat mecanic. Pentru a fi analizate dependenţele dintre tensiuni şi deformaţiile specifice în cazul stărilor spaţiale de tensiuni, se vor imagina, pe rând, efectele produse de diversele componente ale tensiunilor asupra unui volum elementar, de formă prismatică, orientat cu muchiile după direcţiile axelor de coordonate.
Dacă se presupune, pentru început (fig. 3.10), că elementul de volum se află doar sub acţiunea tensiunilor σx (pentru a nu complica inutil discuţia, toate tensiunile normale vor fi considerate de întindere) atunci, paralel cu direcţiile axelor de coordonate x, y, z se vor produce numai deformaţii specifice de tip liniar – una de întindere (εx), cea de pe direcţia tensiunii exterioare şi două de comprimare (contracţie transversală), pe direcţiile perpendiculare pe a tensiunii σx. Folosind regulile cunoscute de la stările liniare de solicitare, aceste alungiri specifice pot fi calculate astfel:
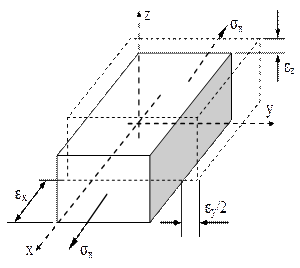 Fig. 3.10 |
Desigur, E şi ν sunt constantele elastice – modulul longitudinal, respectiv coeficientul de contracţie transversală, ale materialului din care este făcut corpul studiat, având aceleaşi valori în orice direcţie din material. În mod analog, dacă volumul elementar este solicitat doar de componentele σy, respectiv σz, alungirile relative pe cele trei direcţii de măsurare sunt:
Dacă elementul de volum este solicitat, simultan, de toate cele trei componente normale de tensiuni, atunci pe fiecare dintre direcţiile axelor de coordonate se vor înregistra câte trei componente de deformaţii specifice liniare, care pot fi adunate algebric, astfel:
(3.23)
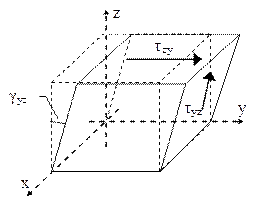 Fig. 3.11 |
Trecând la situaţia în care elementul de volum este solicitat, succesiv, ca singură încărcare (ca în fig. 3.11), de perechile de tensiuni tangenţiale paralele cu planele de coordonate τyz-τzy, τxz-τzx şi τxy-τyx, au loc lunecări specifice pe direcţiile respective şi nu se produc nici un fel de deformaţii liniare, adică efectele produse în cele trei cazuri vor fi calculate astfel:
(3.24)
Desigur, în aceste relaţii se recunoaşte notaţia G, modulul de elasticitate transversal al materialului, iar reunirea expresiilor (3.23) şi (3.24) reprezintă legea lui Hooke, generalizată pentru stările spaţiale de tensiuni, adică pentru situaţia în care sunt nenule toate componentele tensorului Tσ.
Este interesant de observat că, atunci când în relaţiile (3.23) se ia σz = 0, adică starea de tensiuni devine plană, alungirile specifice se vor produce tot pe trei direcţii, adică:
(3.25)
Rezultă că starea de deformaţii nu este tot plană, decât în cazuri particulare!
Pe de altă parte, tot pentru stările plane de tensiuni sunt importante şi folositoare inclusiv relaţiile inverse, de legătură între alungirile specifice şi componentele de tensiuni care le produc, care se calculează astfel:
(3.26)
Observaţii
, care trebuie luate în considerare în calcule (α este o altă caracteristică a materialului – coeficientul de dilatare termică).Deformaţia specifică de volum
Se abordează problema variaţiei relative a volumului prismei elementare de mai sus, atunci când este încărcată simultan cu tensiunile normale σx, σy şi σz, acţionând pe direcţiile axelor de coordonate. Dacă se admite că laturile prismei aveau, înainte de aplicarea încărcărilor, dimensiunile dx, dy şi dz, atunci după solicitare acestea vor creşte cu mărimile alungirilor specifice de pe direcţiile respective, iar noile lor mărimi vor putea fi folosite la calculul volumului modificat al prismei elementare:
Ţinând seama că produsele între două sau mai multe cantităţi infinit mici (aşa cum sunt toate lungimile din această relaţie) au mărimi neglijabile (ca „infiniţi mici de ordin superior”), membrul drept al relaţiei rămâne să conţină numai patru termeni, astfel:
Deoarece volumul iniţial al prismei era dat de produsul laturilor sale (Vin = dx·dy·dz), variaţia relativă de volum, numită şi deformaţie specifică de volum se calculează astfel:
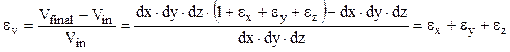(3.27)
Dacă în ultima expresie se folosesc relaţiile (3.23), atunci deformaţia volumică poate fi scrisă şi în funcţie de tensiunile normale care produc solicitarea descrisă:
(3.28)
O situaţie specială este reprezentată de compresiunea hidrostatică, produsă prin tensiunea p, în care starea de solicitare este caracterizată de egalitatea celor trei tensiuni normale principale: σ1 = σ2 = σ3 = -p, de unde rezultă:
Pe această bază se defineşte, prin analogie cu modulul de elasticitate care apare în scrierea legii lui Hooke, caracteristica de material numită modul cubic de elasticitate, care se notează cu litera K şi reprezintă factorul de proporţionalitate între deformaţia volumică şi tensiunea de compresiune:
(3.29)
Pe de altă parte, expresia de mai sus a lui εv în cazul presiunii hidrostatice arată că, dacă factorul ν ar fi singurul variabil în acea relaţie, atunci variaţia de volum ar fi nulă pentru un material care să aibă coeficientul de contracţie transversală ν = 0,5 (un astfel de material este cauciucul). Pentru materialele caracterizate de valori mai mici ale acestui factor, aşa cum sunt cele mai multe dintre materialele uzuale, vor exista variaţii de volum, deşi de mărimi foarte mici, aşa cum sunt şi deformaţiile relative uzuale.
Expresiile generale ale energiei de deformare elastică
S-a arătat anterior, în cadrul studiului solicitărilor simple, că energia specifică de deformare elastică, adică aceea care revine unităţii de volum din materialul solicitat într-un mod oarecare se exprimă în mod distinct, în funcţie de modul în care se produce încărcarea. Astfel, solicitările produse prin tensiuni normale introduc într-o astfel de expresie termeni de tipul 
, iar cele date de tensiuni tangenţiale termeni ca 
.
Pentru starea generală de solicitare, rezultată din însumarea efectelor unor stări elementare, cu tensiuni normale şi tangenţiale orientate după direcţiile axelor de coordonate ataşate elementului de volum, se obţine:
Dacă se înlocuiesc, în această relaţie, expresiile deformaţiilor specifice date de legea generalizată a lui Hooke, notate cu (3.23) şi (3.24), se ajunge la următoarea exprimare a energiei specifice de deformare elastică:
(3.30)
Dacă axele de referinţă se aleg chiar pe direcţiile principale ale stării de tensiuni, atunci tensiunile tangenţiale vor lipsi şi expresia devine:
(3.31)
Odată obţinută această expresie, folosind un volum elementar reprezentativ pentru starea de tensiuni studiată, energia totală de deformare elastică acumulată în corpul solid respectiv, în urma solicitării lui (de tip elastic) prin încărcările mecanice pe care trebuie să le preia, se va putea calcula ca:
.
Energia specifică de deformare modificatoare de formă
Pentru modelarea mai detaliată a fenomenelor de deformare elastică în cazul corpurilor solide solicitate mecanic se admite că o parte din energia totală de deformare este consumată pentru modificarea de volum a corpului deformat, partea rămasă fiind cheltuită pentru schimbarea formei corpului în urma deformării.
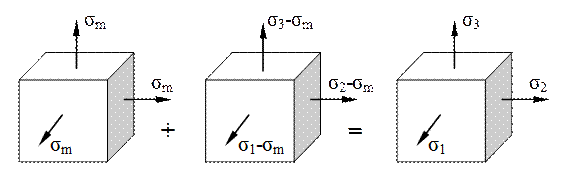 Fig. 3.12 |
Separarea imaginară a celor două tipuri de procese energetice se poate face considerând că starea de solicitare dată prin tensiunile normale principale σ1, σ2 şi σ3 este obţinută prin însumarea a două stări elementare (fig. 3.12), de asemenea orientate pe direcţiile principale ale tensiunilor normale.
În prima stare toate tensiunile principale sunt egale între ele şi egale cu media σm a tensiunilor din starea reală (valoare medie despre care s-a arătat că este egală cu tensiunea octaedrică):
În această situaţie alungirile relative se produc la fel în toate direcţiile, ceea ce înseamnă că forma prismei elementare nu se schimbă în urma solicitării, iar energia de deformare se consumă doar pentru modificarea volumului elementar! Prin urmare, introducând parametrii acestei stări de tensiuni în relaţia (3.31) se va obţine energia specifică modificatoare de volum, astfel:
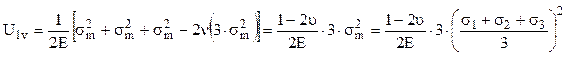
sau, în forma finală 
(3.32)
În cea de-a doua stare elementară, pe feţele volumului elementar acţionează tensiuni principale egale ca mărime cu diferenţa între tensiunile reale şi valoarea lor medie, aşa cum se arată în figura de mai sus.
Dacă pentru această solicitare se calculează, folosind relaţia (3.28), deformaţia specifică de volum, se obţine că:
Aşadar, se poate admite că această combinaţie de tensiuni nu produce schimbări ale mărimii volumului elementar, în schimb îi afectează forma, iar înlocuind valorile tensiunilor în relaţia generală (3.31) se obţine expresia energiei specifice de deformare modificatoare de formă:
După înlocuirea tensiunii medii prin valoarea ei şi reducerea termenilor asemenea se ajunge la forma concentrată a expresiei:
(3.33)
Aceste expresii sunt importante, de exemplu, în stabilirea criteriilor de rupere folosite în inginerie, aşa cum se va arăta în continuare.
Relaţia dintre constantele elastice ale materialelor izotrope
Se imaginează o placă dreptunghiulară, de grosime constantă, dintr-un material omogen şi izotrop, aflată într-o stare plană de tensiuni, sub acţiunea unor încărcări de întindere, pe una dintre direcţiile principale, respectiv de compresiune, pe cealaltă direcţie principală. Pentru simplitate, se admite că tensiunile produse de cele două solicitări (tensiunile principale ale stării de tensiuni din material) au mărimi egale (dar semne contrare!), notate cu σ0.
S-a arătat anterior că o astfel de încărcare produce în placă o stare de forfecare pură, în elementele de volum mărginite de plane înclinate la 45° faţa de direcţiile principale ale tensiunilor normale (fig. 3.12) (pe care tensiunile tangenţiale sunt nule!). Acest lucru poate fi constatat dacă se calculează, folosind relaţiile (3.4), tensiunile de pe planele înclinate la unghiul α = 45°, astfel:
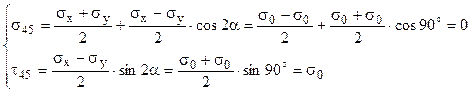
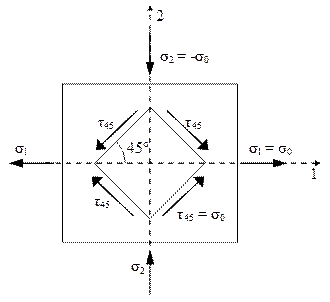 Fig. 3.13 |
Se observă că sunt îndeplinite condiţiile stării de forfecare pură, în sensul că tensiunile normale sunt nule, iar cele tangenţiale egalează în mărime tensiunile principale ce produc întindere şi compresiune pe elementul iniţial.
Componentele de tensiuni din cele două grupări exprimă în fapt aceeaşi solicitare, adică energia specifică de deformare elastică trebuie să aibă aceeaşi mărime pentru amândouă.
Dacă se exprimă în funcţie de tensiunile normale principale, energia specifică de deformare este: 
Pentru elementul decupat oblic, energia specifică se calculează simplu:
Din egalarea celor două variante de exprimare a energiei rezultă relaţia cunoscută între valorile celor trei constante elastice ale unui material omogen şi izotrop: E = 2 (1 + ν) G
Adesea se foloseşte această condiţie pentru stabilirea modulului transversal G atunci când se cunosc celelalte două constante ale materialului cercetat. De exemplu, pentru oţelurile obişnuite se admite că ν = 0,3 şi că modulul longitudinal este E = 210GPa, de unde se obţine G = 81GPa.
