Analiza stărilor de tensiuni pe care diversele tipuri de solicitări le produc în volumul unui corp solid contribuie la stabilirea felului în care corpul se va comporta sub acţiunea încărcărilor sale. Unul dintre scopurile principale ale acestei analize este de a se estima nivelul de încărcare la care devine posibilă încetarea comportării stabile şi reversibile a acelui corp şi eventuala lui scoatere din funcţiune.
În cazul solicitărilor simple, momentul în care materialele nu mai suportă în condiţii corecte încărcările pe care sunt destinate să le preia, adică „cedează”, este relativ uşor de stabilit, pentru că este asimilat cu atingerea unei limite maxime admise (numită de obicei rezistenţă admisibilă a materialului la solicitarea dată), de către cea mai mare tensiune produsă în piesele concrete.
Graniţa superioară a domeniului tensiunilor permise se alege mai mică de un număr c de ori (coeficientul de siguranţă adoptat pentru solicitarea respectivă) decât limita de curgere (pentru materialele tenace şi ductile), respectiv de rupere (pentru cele fragile) a materialului piesei, valori care se stabilesc prin determinări experimentale numite încercări mecanice.
Mult mai dificilă este stabilirea unui nivel periculos al încărcărilor în cazurile, foarte frecvente în practica inginerească, în care corpul analizat trebuie să preia mai multe solicitări simple simultan, adică este supus unor solicitări compuse. Este practic imposibilă efectuarea unor încercări mecanice pentru gama foarte largă de stări de tensiuni posibile, acestea având adeseori un grad mare de complexitate. Ar fi necesare, chiar şi pentru studiul unui singur material, încercări foarte multe, pe maşini de construcţii complicate şi cu epruvete numeroase şi greu de executat.
Acestea sunt motivele pentru care a devenit necesară o metodă de aproximare a stărilor limită, prin care să se echivaleze gradul de pericol pe care îl prezintă, pentru integritatea corpului studiat, solicitarea lui compusă, cu nivelele periculoase ale unei solicitări simple monoaxiale. Mai precis, să poată fi folosită rezistenţa admisibilă, stabilită prin încercarea la tracţiune, în calculul referitor la stări de tensiuni plane sau spaţiale.
Este important de semnalat că intensitatea solicitărilor dintr-un punct oarecare al corpului tensionat poate fi caracterizată prin mărimi fizice foarte diferite, precum tensiunea normală maximă (σmax), alungirea specifică maximă (εmax), tensiunea tangenţială maximă (τmax), energia specifică de deformare elastică acumulată (U1ef) s.a.m.d.
Diversele teorii de rupere se particularizează tocmai prin alegerea uneia dintre aceste mărimi (care dă şi numele teoriei) ca determinantă pentru pierderea capacităţii materialului de a suporta încărcările exterioare ale corpului studiat. Mai precis, se consideră că probabilitatea cedării atinge un maxim atunci când una anume dintre mărimile menţionate egalează nivelul ei considerat periculos pentru starea monoaxială de tensiuni luată ca reper.
Teoriile au fost elaborate de autori diferiţi, în momente diferite ale istoriei şi ale evoluţiei cercetărilor inginereşti, astfel încât criteriile la care se ajunge pe baza lor cresc în complexitate, de la prima teorie către ultima dintre cele ce se vor enunţa mai jos. Trebuie precizat faptul că nici una dintre acestea nu este potrivită, în aceeaşi măsură, pentru orice fel de stare de tensiuni sau de solicitare, astfel că se menţionează, în fiecare caz, pentru care situaţii practice se recomandă folosirea criteriului respectiv.

Enunţarea celor mai importante teorii de rupere

O stare complexă de tensiuni este la fel de periculoasă, pentru integritatea corpului solid în care se produce, ca şi starea determinată de o solicitare de întindere uniaxială, atunci când una dintre următoarele mărimi fizice are aceeaşi valoare în cele două stări de tensiuni:

I. Tensiunea normală maximă    (atribuită lui Galileo Galilei, sec. XVII)

Se consideră că tensiunea principală σ1 (respectiv σ3, dacă aceasta are valoarea absolută maximă) este cea care favorizează cedarea materialului, în momentul în care atinge nivelul considerat periculos pentru întinderea uniaxială a unei epruvete din materialul respectiv.
Această teorie are dezavantajul că desconsideră influenţa pe care o au, pentru funcţionarea stabilă şi reversibilă a corpului analizat, două din cele trei tensiuni normale principale ale stării de tensiuni. De aici provine, probabil, faptul că estimările bazate pe această teorie sunt confirmate practic doar pentru o clasă de materiale, cele foarte fragile (piatră, cărămidă, oţel de scule, ceramice etc.)

II. Alungirea specifică maximă                             (E.Mariotte, 1682)

Se admite că deteriorarea materialului începe atunci când, într-un punct oarecare din volumul corpului studiat, alungirea specifică εmax atinge (în termeni absoluţi) valoarea din momentul cedării epruvetei solicitate la întindere monoaxială.
Teoria aduce noutatea corelării efectelor produse de cele trei tensiuni normale principale şi se dovedeşte utilizabilă pentru o grupare mai largă de materiale fragile (fonte aliate, oţeluri aliate de înaltă rezistenţă); în schimb, nu poate fi aplicată pentru materialele care, atunci când sunt deformate elastic, nu respectă legea lui Hooke, sau care se află, în starea de tensiuni analizată, dincolo de limita lor de proporţionalitate de pe curba caracteristică la solicitarea respectivă.

III. Tensiunea tangenţială maximă      (Ch.Coulomb, 1773; Tresca, 1865)

Se enunţă asemănător cu prima teorie, este considerată potrivită pentru materialele care se comportă la fel, când sunt solicitate la întindere şi la comprimare. Este criticabilă pentru că neglijează efectele valorii mediane σ2 a tensiunilor principale.
Se consideră că exprimă cel mai bine (şi fără să fie influenţată de domeniul elastic şi de respectarea de către material a legii lui Hooke) momentul de început al „curgerii” (dacă aceasta există), în care apar în material deformaţiile plastice, atunci când este atinsă o valoare anume a tensiunilor tangenţiale din material. Ca urmare, criteriul σech III = σc este adoptat adesea, drept condiţie de cedare, pentru materialele metalice.

IV. Energia potenţială specifică de deformare elastică (E.Beltrami, 1885)

Este stabilit ca periculos momentul în care, în dreptul unui punct arbitrar din volumul corpului studiat, energia specifică U1 atinge valoarea din starea periculoasă a epruvetei solicitate la tracţiune uniaxială.
Se dovedeşte potrivită cu realitatea pentru metalele tenace şi pentru stările de tensiuni în care valoarea medie σoct a tensiunilor principale este pozitivă (starea de tensiuni este preponderent de întindere). Dacă această valoare este negativă (adică pentru stările de tensiuni cu comprimare preponderentă), se foloseşte în calcule criteriul dat de teoria următoare.

V. Energia potenţială specifică de modificare a formei
(M.T.Huber, H.Hencky, R. von Mises)
Criteriul bazat pe această teorie este utilizat pe scară largă în modelarea numerică a stărilor de tensiuni, mai ales în situaţiile cu σoct < 0. Se porneşte de la observaţia că materialele suportă mai bine compresiunea hidrostatică (egal distribuită triaxial) – care produce doar modificare de volum, nu şi de formă, faţă de cea monoaxială, care modifică în mod clar şi forma epruvetelor. Prin urmare, hotărâtoare pentru cedare ar fi atingerea acelui nivel al energiei specifice U1f care se acumulează, în momentul cedării, în epruveta din acel material solicitată la compresiune monoaxială.

Exprimarea criteriilor de rupere

Aceste criterii pun în legătură mărimea fizică (aici introdusă pentru prima oară pentru caracterizarea unei stări de solicitare) numită tensiune echivalentă σech cu parametrii reali ai stării de tensiuni vizate. Se obţin prin egalarea cu valoarea din starea monoaxială considerată egal de periculoasă, a expresiei cu care se calculează mărimea desemnată prin teoria respectivă, pentru starea complexă de tensiuni care se analizează.
În mod practic se folosesc, aşa cum se arată mai jos, câteva dintre relaţiile de calcul stabilite în capitolul anterior, puse în corespondenţă cu particularizarea lor pentru o stare liniară de tensiuni, produsă prin solicitarea monoaxială echivalentă.

Egalând mărimile din ultimele coloane şi de pe o aceeaşi linie se ajunge la relaţiile de calcul pentru tensiunile echivalente date de cele 5 teorii, astfel:

Aceste relaţii sunt folosite pentru finalizarea calculelor la solicitările compuse: condiţia de rezistenţă se scrie pentru starea de tensiuni cea mai periculoasă (cu tensiunile principale cele mai mari), dintre cele care se produc în diverse puncte din volumul corpului studiat.
Folosind parametrii acelei stări de tensiuni şi criteriul dat de teoria de rupere cea mai potrivită cu starea de solicitare analizată, se calculează tensiunea echivalentă din punctul respectiv. Calculul de rezistenţă se bazează pe condiţia ca acest σech să nu depăşească rezistenţa admisibilă σa a materialului dat, stabilită prin încercarea lui la solicitarea monoaxilaă respectivă.

Teoria stării limită (O.Mohr)

Pornind de la teoria tensiunii tangenţiale maxime şi de la reprezentarea grafică (propusă de Otto Mohr) a stărilor de tensiuni, a fost elaborat un criteriu de cedare valabil pentru materialele care au rezistenţa la comprimare mai mare decât aceea la întindere. Teoria III se bazează, în reprezentarea cu cercuri Mohr, numai pe cercul cu diametrul cel mai mare al stării de tensiuni analizate (raza acelui cerc este valoarea lui τmax).
Prin urmare, dacă într-un acelaşi sistem de axe (fig. 4.1) se trasează cercurile care corespund limitelor de curgere ale materialului considerat pentru cele trei solicitări simple de bază – tracţiune şi comprimare uniaxială, respectiv forfecare pură – atunci stările de tensiuni permise pentru acel material sunt delimitate de înfăşurătoarea celor trei cercuri de mai sus.

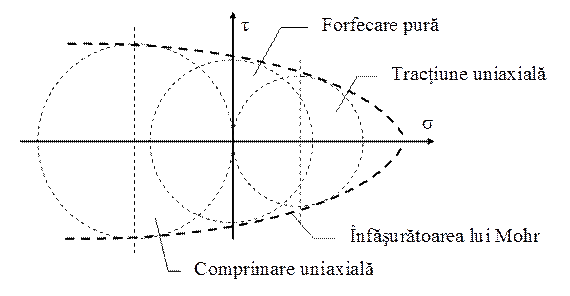Fig. 4.1

Prin urmare, vor fi considerate suportabile acele stări de tensiuni pentru care reprezentările grafice prin cercuri Mohr se vor plasa în interiorul curbei de înfăşurare de pe grafic, excluzând pe cele tangente la aceasta.

Fig. 4.2

   Criteriul de cedare pentru această teorie se obţine de pe o variantă simplificată a curbei de înfăşurare, bazată pe doar două cercuri, care au ca diametre valorile limitelor de curgere – la tracţiune σct, respectiv la comprimare σcc de pe curbele caracteristice ale materialului studiat.
Folosind câteva relaţii geometrice între razele cercurilor din fig. 4.2 se scrie că:

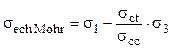
Trebuie observat că, pentru materialele care se comportă asemănător la tracţiune şi la comprimare, fracţia din membrul drept ajunge la valoarea 1 şi se obţine aceeaşi tensiune echivalentă ca la teoria τmax de mai sus.

Particularizări pentru stările plane de tensiuni

După cum a rezultat din paragrafele precedente, criteriile de rupere conduc la relaţii diferite pentru calculul de rezistenţă; acestea se obţin limitând valorile tensiunii σech prin rezistenţa admisibilă a materialului la solicitările monoaxiale de tracţiune σat, respectiv de comprimare σac.
Folosind relaţiile, date anterior pentru fiecare criteriu, ale tensiunii echivalente, particularizate pentru stările de tensiuni în care σ3 = 0, se obţin condiţiile de rezistenţă care corespund stărilor plane, pentru fiecare dintre teoriile de rupere descrise mai sus:

Observaţii

1. Primele două criterii sunt exprimate prin câte două condiţii deoarece nu se poate afirma cu precizie care dintre mărimile cuprinse între inegalităţi are cea mai mare valoare şi atunci ambele sunt limitate.
2. La al treilea criteriu, dacă cele două valori principale au acelaşi semn, atunci σ3 = 0 nu este cuprins între ele şi τmax rămâne egal cu σ1 sau cu σ2. Dacă au semne diferite, atunci criteriul duce la limitarea diferenţei lor.

Aceste relaţii de calcul pot fi folosite în rezolvarea oricărei probleme cu privire la o stare plană de tensiuni, desigur alegând criteriul cel mai potrivit pentru materialul corpului solid studiat.
Este interesant şi util să se compare eficienţa acestor condiţii pentru siguranţa în exploatare a piesei proiectate pe baza lor. În acest scop, folosind sistemul de axe σ1 – σ2, se reprezintă grafic limitările impuse de inegalităţile prin care sunt date cele cinci criterii, cu referire la un material care se comportă la fel la întindere şi la comprimare (σat = σac = σa).

Fig. 4.3

Trebuie precizat că, pe această reprezentare, orice stare concretă de tensiuni va fi simbolizată printr-un singur punct, având coordonatele date de valorile tensiunilor ei principale. Pentru a stabili unde se plasează stările de tensiuni periculoase pentru materialul dat, se urmăresc graniţele formate de condiţiile fiecărui criteriu de rezistenţă.
Astfel, limitele date de criteriul I formează un pătrat, cele de la criteriul II un romb, alungit pe direcţiile cadranelor trigonometrice I şi III, pentru criteriul τmax se obţin două linii înclinate la 45°, în cadranele unde σ1 şi σ2 au semne contrare, plus segmentele drepte de la primul criteriu, în cadranele unde au acelaşi semn. Prin urmare, se formează un hexagon turtit, neregulat, marcat pe desen cu linii groase întrerupte.
Pentru criteriile energetice IV şi V graniţele au forme de elipse, cu diagonalele principale pe direcţia de alungire a rombului de la criteriul II şi cu observaţia că elipsa de la criteriul ultim este ceva mai alungită, faţă de cea de la criteriul IV.
Pe desen mai este arătat, schematic, faptul că pe axele de coordonate se poziţionează stările monoaxiale (liniare) de întindere, respectiv de comprimare, iar pe diagonalele sistemului de axe – solicitările biaxiale uniforme, respectiv stările de forfecare pură.
Se înţelege că punctele situate în interiorul domeniilor obţinute respectă, prin coordonatele lor, condiţiile de rezistenţă la care se referă (deci reprezintă stări de solicitare sigure), cele aflate chiar pe graniţe făcând să apară semnul egal în acele condiţii. Despre stările de tensiuni simbolizate în afara tuturor domeniilor se conchide că sunt periculoase pentru material şi trebuie evitate.
Punctele aflate între graniţele exterioare şi cele interioare se referă la stări nesigure, pentru care sunt respectate unele condiţii, nu şi altele; decizia de a admite o astfel de solicitare trebuie luată în funcţie de material şi de criteriul despre care se consideră că i se potriveşte cel mai bine.
Reprezentarea din figura 4.3 permite afirmaţia că există criterii de siguranţă maximă: acestea sunt criteriul τmax – pentru stările cu tensiuni principale de semne contrare, respectiv σmax – pentru celelalte stări (cu precizarea că, pentru solicitările apropiate de stările biaxiale uniforme, criteriul IV dă graniţe care pot fi aproximate de criteriul I). Este însă bine de observat că în afara acestor graniţe sigure rămân o mulţime de stări de tensiuni care sunt admisibile, după celelalte criterii, iar renunţarea la ele, ca solicitări permise, duce la neutilizarea completă a capacităţii de rezistenţă a materialului şi la supradimensionări ale pieselor proiectate.
Mai trebuie remarcată distanţa la care se găsesc, faţă de celelalte domenii, graniţele date de criteriul I – pentru stările cu tensiuni principale de semne opuse, respectiv de criteriul II – pentru stările cu tensiuni principale de acelaşi semn; ele sunt criteriile de cea mai mică siguranţă, pentru acele situaţii de solicitare, deci vor fi evitate.

Particularizări pentru stările de tensiuni cu σy = 0

Astfel de stări de tensiuni se întâlnesc destul de frecvent în practică, fiind caracteristice, de exemplu, pentru barele solicitate simultan la încovoiere şi la răsucire. Pentru simplificarea scrierii, în cele ce urmează se adoptă notaţiile:                               σx = σ   şi   τxy = τ

Tensiunile normale principale se vor calcula folosind relaţiile clasice:

Pe această bază, criteriile de rupere vor da următoarele relaţii pentru σech:
I) criteriul σmax

II) criteriul εmax

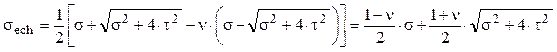
Ultima relaţie poate fi încă particularizată, dacă se admite că materialul pentru care se face calculul este un metal, având coeficientul de contracţie transversală de valoare aproximativă   ν = 0,3   pentru care se obţine:

III) criteriul τmax

IV) criteriul U1

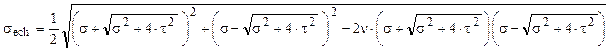
După efectuarea operaţiilor de sub radical şi reducerea termenilor asemenea se ajunge la următoarea expresie:

Particularizarea pentru metale cu   ν = 0,3   duce la relaţia finală:

V) criteriul U1f

Procedând la fel ca mai sus se obţine că:

de unde relaţia finală se scrie:

Este remarcabilă similitudinea relaţiilor date de ultimele 3 criterii, care se deosebesc numai prin valoarea coeficientului care apare sub radical. Luând în considerare argumentele discutate anterior, calculele de rezistenţă se fac cel mai frecvent pe baza teoriei τmax, despre care se observă că duce şi la valoarea cea mai mare pentru σech, dintre cele 3 criterii care au relaţii similare. Totuşi, nu este de neglijat necesitatea de a se analiza eventualitatea ca unul dintre celelalte două criterii să fie mai potrivit cu materialul şi situaţia de solicitare din problema concretă care se abordează, întrucât o valoare mai mică pentru tensiunea echivalentă va conduce la dimensiuni mai zvelte ale piesei proiectate şi deci la economii de material.

Posibilitatea de evaluare a tensiunilor tangenţiale admisibile

O problemă conexă cu cele discutate în paragraful anterior este legată de obţinerea, pe baza relaţiilor de mai sus ale tensiunii echivalente, a unor estimări ale valorilor rezistenţelor admisibile τa ale materialelor, pentru solicitările produse prin tensiuni tangenţiale, atunci când li se cunosc valorile σa pentru întinderea uniaxială. Astfel de evaluări sunt foarte utile, întrucât nu mai este necesară realizarea unor încercări mecanice de forfecare pură, destul de greu de pus în practică.
Se porneşte de la relaţia lui σech pentru fiecare criteriu de cedare (cu valoarea coeficientului de contracţie al materialelor metalice ν = 0,3), în care se face şi σx = σ = 0, adică se abordează o stare de tensiuni dată doar prin tensiunile tangenţiale τxy (forfecare pură), apoi se scrie condiţia clasică de rezistenţă, din care va rezulta valoarea maximă permisă a tensiunilor tangenţiale, care este tocmai rezistenţa admisibilă τa.

I) criteriul σmax

II) criteriul εmax

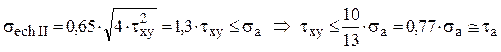
Se reaminteşte că acest criteriu este considerat adecvat pentru calculul de rezistenţă în cazul materialelor fragile. De aici rezultă că ultima estimare a lui τa este valabilă pentru materialele care se rup casant, prin forfecare.
III) criteriul τmax

IV) criteriul U1

V) criteriul U1f

Se observă că, lăsând deoparte primul criteriu, utilizabil pentru o gamă relativ restrânsă de aplicaţii, ca şi pe cel de-al doilea, deja discutat mai sus, se obţine recomandarea ca valorile τa să fie cuprinse, ca fracţii din σa, între 0,5 şi 0,62. Alegerea finală se poate baza, de exemplu, pe ipoteza de rupere recomandată pentru materialul piesei care se calculează.