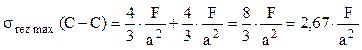 Fig. 5.1 |
Capitolele anterioare s-au referit la încărcări, aplicate barelor drepte, la care eforturile apărute în secţiunile transversale (cele importante pentru calculele de rezistenţă) erau de un singur fel, adică aveau o singură componentă, dirijată fie pe direcţia axei longitudinale a barei, fie a uneia dintre axele principale centrale ale secţiunilor ei.
Astfel de solicitări se numesc simple şi au particularitatea că sunt lipsite de echivoc în privinţa stabilirii tensiunilor care pun în pericol integritatea barei, precum şi a valorii lor maxime, care trebuie introdusă în relaţia calculului de rezistenţă.
Prin contrast, există foarte multe situaţii practice în care solicitările sunt compuse, adică în secţiuni apar eforturi şi tensiuni de cel puţin două categorii diferite; acestea sunt analizate separat, pentru stabilirea punctelor din bară în care se produc cele mai mari tensiuni, după care în acele puncte sunt calculate efectele globale, în două feluri distincte:
a) dacă toate tensiunile elementare sunt de aceeaşi natură şi la fel orientate în raport cu secţiunile transversale, atunci valorile lor dintr-un acelaşi punct al barei pot fi adunate algebric, rezultatul acestei operaţii fiind numit tensiune rezultantă σrez(x) sau τrez(x);
b) dacă respectivele tensiuni sunt orientate diferit sau au naturi diferite, atunci sumarea algebrică nu mai este posibilă şi efectul global este calculat ca o tensiune echivalentă σech(x), folosind una dintre teoriile de rupere.
La finalul acestor operaţii, valoarea cea mai mare a tensiunii globale se introduce în relaţia calculului de rezistenţă, adică se compară cu rezistenţa admisibilă, aleasă conform cu felul respectivei tensiuni globale, a materialului din care este făcută bara.
Calculele de rigiditate, referitoare adică la deplasările şi deformaţiile unor puncte şi segmente de puncte din bara analizată, se fac după aceleaşi principii ca la solicitările simple, cu mari precauţii pentru luarea în considerare a efectelor de deformare produse de toate solicitările elementare care se produc simultan în bară.
Paragrafele care urmează vor aborda, succesiv, principalele categorii de solicitări compuse întâlnite în calculele inginereşti. Începutul se face cu solicitările care fac apel direct la cunoştinţele privind stările de tensiuni cu parametrii σx şi τxy, abordate în finalul capitolului anterior.
A. Solicitări de tip (σ + τ)
Încărcările cuprinse în această categorie produc simultan, în toate punctele din (cel puţin) anumite secţiuni transversale ale barei, tensiuni de două naturi diferite, adică normale şi tangenţiale. Indiferent cum sunt orientate, acestea nu pot fi vreodată adunate algebric, efectele lor globale fiind calculate exclusiv pe baza uneia dintre teoriile de rupere.
Pentru barele uzuale efectele produse prin solicitarea de forfecare sunt de obicei puţin semnificative, ca intensitate, în raport cu cele produse prin încovoiere sau prin întindere-comprimare, astfel încât cel mai frecvent se combină solicitările de încovoiere şi de răsucire.
În acest context trebuie reamintit că nu a fost încă abordată răsucirea barelor de secţiuni necirculare, pentru care însă rămân valabile toate principiile folosite în această prezentare. Pe de altă parte, atunci când încovoierea şi răsucirea sunt aplicate simultan barelor cu secţiuni circulare, relaţiile cu care se calculează tensiunile echivalente pot fi aduse la forme foarte interesante, care apropie această solicitare compusă de calculul la încovoierea simplă.
Prin urmare, se consideră o secţiune transversală oarecare, de formă circulară plină, cu diametrul d, dintr-o bară solicitată la răsucire şi la încovoiere, eforturile din secţiunea aleasă fiind momentele Mt(x) – orientat pe direcţia axei longitudinale, respectiv Miz(x) – pe axa principală centrală orizontală a secţiunii.
| Fig. 5.1 |
Tensiunile produse de cele două solicitări sunt simultan maxime în două puncte ale secţiunii, cele de la capătul diametrului ei vertical (fig. 5.1), iar valorile lor absolute se scriu:
Punctele respective sunt cele mai solicitate din secţiune, deci acolo trebuie calculată tensiunea globală maximă, cu una dintre teoriile de rupere.
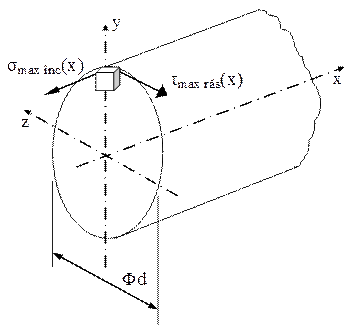
S-a arătat anterior că criteriile folosite cel mai frecvent sunt cele cu numerele III, IV şi V, pentru care relaţiile cu care se calculează σech diferă între ele doar prin coeficientul k de sub radical:
(5.1)
Acest coeficient are valorile 4, 2.6 şi respectiv 3, iar această situaţie conduce la posibilitatea de a se scrie într-o formă compactă relaţia finală pentru calculul tensiunii echivalente maxime, pentru toate cele trei criterii amintite.
În acest scop, se introduc în formula (5.1) expresiile, date mai sus, ale tensiunilor maxime, după care se ţine seama că modulii de rezistenţă la încovoiere şi la răsucire nu sunt independenţi între ei, în cazul secţiunilor circulare, adică:
Prin urmare, relaţia căutată se scrie astfel:
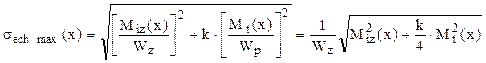
Se observă că ultimul radical poate fi asimilat cu un moment echivalent de încovoiere Mi ech(x), astfel încât relaţia calculului de rezistenţă, pentru solicitarea compusă de încovoiere şi răsucire, la barele de secţiuni circulare (pline sau inelare), poate fi scrisă sub forma de la încovoierea simplă:
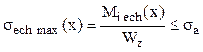(5.2)
Particularizarea pentru fiecare dintre cele trei criterii de rupere se face prin intermediul momentului echivalent, calculat astfel:
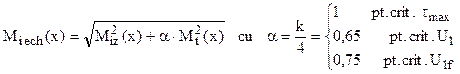(5.3)
Alegerea criteriului potrivit, pentru o situaţie dată de solicitare, se face în funcţie de materialul piesei calculate. Cel mai frecvent este folosită varianta bazată pe criteriul τmax, în special pentru piesele din materiale tenace.
Pentru a putea evalua, chiar şi orientativ, diferenţele dintre rezultate, în cadrul rezolvării aplicaţiei de mai jos se vor face calculele de rezistenţă cu toate cele trei variante ale relaţiei (5.3), după care se vor analiza comparativ dimensiunile astfel obţinute.
Calculele pentru această categorie de solicitări compuse vor fi ilustrate prin două aplicaţii tipice, dintre cele frecvent întâlnite în practică: o bară cotită încărcată cu o forţă perpendiculară pe planul ei şi un arbore de transmisie, dintr-un reductor de turaţie.
Aplicaţii
5.1. Se consideră o bară cotită de forma literei L, încastrată la un capăt şi liberă la celălalt (fig. 5.2), unde acţionează forţa concentrată F = 2kN, orientată perpendicular pe planul în care se află axa longitudinală a barei.
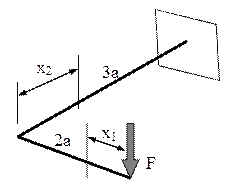 Fig. 5.2 |
Secţiunile transversale sunt aceleaşi pe toată lungimea, circulare pline cu diametrul d, iar lungimile celor două segmente sunt marcate pe desen în funcţie de parametrul a = 0,2m.
Se cere să se dimensioneze bara, cunoscând că este din oţel, cu caracteristicile σa = 160 şi E = 21·104 [MPa]; să se mai calculeze şi cu ce distanţă se deplasează, pe verticală, secţiunea de la capătul barei, în care acţionează forţa exterioară F.
Rezolvare
a) Dimensionarea barei
Trebuie analizate mai întâi eforturile secţionale din bară, la fel cum se procedează la solicitările simple. Dacă se admite că axa x rămâne mereu dispusă pe axa longitudinală, rezultă ca axa verticală y este neschimbată, ca direcţie, pe întreaga bară, în vreme ce axa orizontală z se roteşte cu 90°, odată cu axa x (pe care este perpendiculară), în secţiunea de la cotitura barei. Se observă că forţa F se proiectează numai pe axa y, adică efectele ei de tip forţă vor fi exclusiv tăietoare (de mărimi egale peste tot cu F), care practic nu influenţează calculele de rezistenţă ale barei.
Pe desen au fost deja marcate cele două secţionări imaginare ce vor fi folosite la calculul momentelor secţionale. Pe prima regiune se produce moment doar în raport cu axa z, adică numai încovoiere în plan vertical, în vreme ce pe regiunea a doua apar momente atât faţă de axa z, cât şi faţă de axa barei x, adică are loc solicitarea compusă de încovoiere cu răsucire.
Eforturile secţionale se calculează astfel:
a) x1 € (0, 2a): Miz(x1) = - F·x Miz(0) = 0, Miz(2a) = - 2aF
b) x2 € (0, 3a): Miz(x2) = - F·x Miz(0) = 0, Miz(3a) = - 3aF
Mt(x2) = 2aF = ct
Reprezentările grafice ale acestor rezultate (diagramele de momente) sunt schiţate mai jos. Se observă că solicitarea periculoasă a barei are loc în secţiunea ei din încastrare, unde momentul de încovoiere atinge valoarea lui maximă. Această valoare va fi introdusă fără semnul minus, în relaţiile (5.3), cu care se calculează Mi ech(x), întrucât în toate acele variante eforturile secţionale apar la puterea a doua.
  |
Prin urmare, momentul echivalent maxim de pe bara considerată este:
În funcţie de criteriul de rupere ales, valorile acestei mărimi vor fi:
- pentru criteriul τmax 
- pentru criteriul U1 
- pentru criteriul U1f 
Valoarea cea mai mare se obţine cu criteriul III, iar celelalte două sunt mai mici cu 5,5%, respectiv cu 4%, faţă de cea maximă. Important însă este să se verifice diferenţa între dimensiunile obţinute prin calcule, în cele 3 variante.
În acest sens, dacă se notează cu β factorul care se înmulţeşte cu (aF) în rezultatele de mai sus obţinute pentru Mi ech max, atunci din condiţia (5.2) a calculului de rezistenţă se obţine relaţia de dimensionare, astfel:
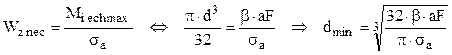
Prin înlocuirea datelor problemei în ultima relaţie se obţine:
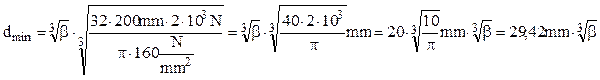
Dimensiunile de calcul după cele trei criterii de mai sus sunt:
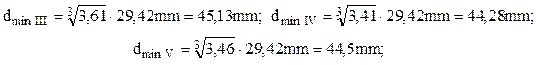
Ultimele două rezultate reprezintă 98,1% şi respectiv 98,6% din primul, adică diferenţa lor faţă de valoarea maximă obţinută este mai mică de două procente, care se încadrează în limitele erorilor acceptabile pentru calculele inginereşti. Rezultă de aici, mai întâi, că oricare dintre cele trei criterii menţionate poate fi utilizat, cu aceeaşi eficienţă, în calculele de rezistenţă de la solicitarea compusă de încovoiere şi răsucire, la secţiunile circulare pline; pe de altă parte, alegerea criteriului τmax, despre care s-a arătat că se foloseşte cel mai frecvent, se dovedeşte şi pe această cale a fi convenabilă.
Ca dimensiune finală a barei studiate se poate alege valoarea dad = 46mm
b) Calculul deplasării verticale la capătul barei
Având în vedere că singura încărcare exterioară a barei este chiar forţa F, în al cărei punct de aplicaţie (notat, în continuare, cu P) şi pe a cărei direcţie trebuie stabilită valoarea deplasării, metoda de calcul cea mai potrivită este cea bazată pe una dintre teoremele lui Castigliano. Luând în considerare solicitările care apar în bară, expresia teoremei este următoarea:
Folosind rezultatele anterioare, calculul propriu-zis se face astfel:
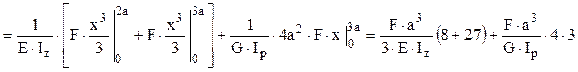
Cunoscând că E = G·2(1+ν) ≈ 2,6·G şi că, pentru secţiunile circulare pline, Ip = 2Iz, ultima expresie devine:
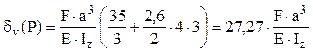
Calculul final se face înlocuind în ultima relaţie datele numerice ale problemei, după care se obţine:
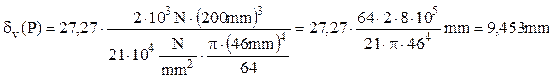
Deplasarea calculată reprezintă o valoare pertinentă, având în vedere dimensiunile barei şi mărimea forţei care i se aplică, astfel încât se poate admite că nu este depăşit domeniul de deformabilitate elastică a materialului său. În plus, se reaminteşte că rezultatul pozitiv al acestui calcul arată că punctul P, în care forţa F acţionează asupra barei, se deplasează vertical în jos, adică în chiar sensul forţei exterioare, ceea ce este evident şi din punct de vedere fizic.
5.2. Se consideră un arbore de transmisie, de secţiune circulară plină cu diametrul d, făcut din oţel cu σa = 160MPa, rezemat prin lagăre de rostogolire (rulmenţi) şi încărcat cu două forţe concentrate care acţionează pe circumferinţa unor roţi, solidarizate pe arbore, aşa cum se arată în desenul alăturat.
Să se dimensioneze arborele, ştiind că a = 100; D1 = 60; D2 = 80 [mm], iar F1 = 2kN.
Rezolvare
Valoarea celei de-a doua forţe exterioare se stabileşte din echilibrul momentelor date de cele două forţe, în raport cu axa arborelui:
Pentru simplificarea scrierii, pe parcursul rezolvării literale a problemei, este util să se introducă un parametru de forţă, notat de exemplu cu F = 0,5kN şi ducând la substituţiile F1 = 4F, respectiv F2 = 3F. În acelaşi scop, se observă că diametrele celor două roţi se pot scrie în funcţie de parametrul a al distanţelor, astfel: D1 = 3a/5, respectiv D2 = 4a/5.
Forţele exterioare acţionează în plane diferite, perpendiculare între ele, care pot fi considerate vertical, respectiv orizontal. Arborele este solicitat la încovoiere în ambele plane şi folosind notaţiile de mai sus se pot face calculele pentru trasarea celor două diagrame de momente.
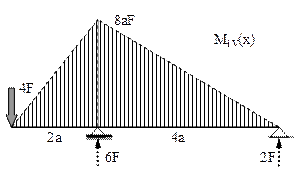
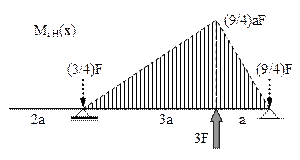
Diagramele au fost schiţate direct pe schemele de încărcare din cele două plane, unde sunt indicate, pentru fiecare caz, inclusiv valorile reacţiunilor din reazeme. Cele două eforturi de încovoiere acţionează în plane perpendiculare între ele şi vor produce, în fiecare secţiune a arborelui, câte un moment de încovoiere rezultant, Mi rez(x), calculat astfel:
Valorile maxime (relative) ale acestei mărimi se pot înregistra fie în dreptul reazemului din stânga, unde MiH(x) = 0, adică Mirez(x) = 8aF, fie în secţiunea (aflată la distanţa a de capătul barei) în care acţionează forţa F2 şi unde MiV(x) = 2aF (un sfert din valoarea maximă a lui MiV). Se obţine deci că în acea secţiune momentul rezultant este:
Această valoare este mult mai mică decât 8aF, care rămâne Mi rez max(x).
Pe de altă parte, datorită faptului că roţile sunt solidarizate pe arbore, cele două forţe care le încarcă tind să rotească arborele în sensuri contrare, adică îl solicită la răsucire (pe lungimea cuprinsă între secţiunile unde sunt montate roţile) cu un moment constant, având valoarea:
În scop orientativ a fost aflată şi valoarea numerică a momentului, deşi în cele de mai jos calculele se vor face tot sub formă literală. Pe de altă parte, pe diagrama de efort au fost marcate şi salturile pe care le determină, la capetele graficului, cele două momente de răsucire concentrate produse de forţele F1 şi F2.
Analizând rezultatele de până acum, se constată că solicitarea periculoasă are loc în secţiunea din reazemul din stânga, unde ambele tipuri de eforturi secţionale ating valorile lor maxime. Relaţia (5.3), bazată pe criteriul τmax, duce la următoarea formă a momentului echivalent maxim:
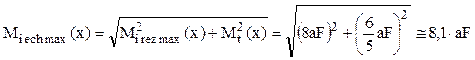
Din condiţia de rezistenţă (5.2) se va scrie că:
Pe această bază, dimensiunea finală a arborelui calculat va fi dad = 30mm.
B. Solicitări de tip (τ + τ)
Gruparea aceasta de solicitări este mult mai slab reprezentată în practică, întrucât rezultă prin suprapunerea unor încărcări care produc forfecare şi răsucire, iar tensiunile tangenţiale de forfecare sunt de obicei mult mai slabe, ca intensitate, în comparaţie cu cele de la răsucire.
Există o excepţie importantă, în această privinţă, care va fi discutată în detaliu în cele ce urmează. Trebuie observat că tensiunile produse de cele două solicitări au aceeaşi natură, adică vor putea fi adunate algebric, pentru că în principiu sunt orientate în acelaşi fel, cel puţin parţial, pe secţiunile de calcul. Se obţine astfel tensiunea rezultantă τrez(x), a cărei valoare maximă se introduce în relaţia calculului de rezistenţă, unde se compară cu rezistenţa admisibilă τa a materialului piesei calculate.
|
Calculul arcurilor elicoidale cu spire strânse
Aceste piese sunt elemente constructive de tip elastic, folosite în diferite aplicaţii inginereşti pentru amortizarea şocurilor şi vibraţiilor, dar şi ca elemente de închidere în diverse tipuri de circuite de comandă sau de siguranţă, hidraulice şi pneumatice. În mod tipic sunt fabricate prin înfăşurarea unor sârme metalice, de obicei din oţeluri aliate (numite chiar oţeluri de arc), foarte rezistente, care formează un număr n de spire, cilindrice sau (mai rar) de alte forme.
Alte caracteristici importante ale arcurilor sunt diametrul d al sârmei şi raza R a înfăşurării (de mărime constantă, la arcul cilindric), care devine raza arcului. Este important şi unghiul α al înfăşurării, în funcţie de care se stabilesc eforturile secţionale importante din spirele de arc.
Astfel, dacă acest unghi este relativ mic (cuprins între 10° şi 30°), arcul se numeşte „cu spire strânse”, iar eforturile de încovoiere care se produc în spire au mărimi neglijabile în raport cu cele date de solicitările de forfecare şi de răsucire. Acestea sunt produse de forţa tăietoare F, având aceeaşi mărime în orice secţiune făcută prin spire, pe direcţia razei arcului, respectiv de momentul de răsucire, de mărime Mt = FR, de asemenea constantă în orice secţiune.
 Fig. 5.4 |
Tensiunile tangenţiale de forfecare τf au direcţie verticală, şi sens opus forţelor F care le produc, iar pe înălţimea oricărei spire se distribuie după o lege parabolică (fig. 5.4), obţinută prin calcule bazate pe relaţia lui Juravski. În acest sens, s-a arătat că tensiunile sunt nule la marginile secţiunii şi ating valoarea maximă pe axa principală centrală a secţiunii care este perpendiculară pe forţele tăietoare F. Pentru secţiunile circulare pline s-a arătat că această valoare este: τmax f = (4/3)·(F/A).
Tensiunile de răsucire τt variază liniar pe orice diametru al secţiunii spirei, având mărimi proporţionale cu distanţele lor până la centrul secţiunii şi sensuri care, prin tendinţa de rotaţie în jurul centrului secţiunii, se opun momentului de răsucire exterior. Valorile maxime sunt τmax t = Mt/Wp şi apar pe circumferinţa secţiunii.
Cele două categorii de tensiuni dau rezultantele cele mai mari atunci când au aceeaşi direcţie, ceea ce se întâmplă numai în punctele situate pe diametrul orizontal AB al secţiunii considerate, la capetele căruia au simultan valori maxime. Sensurile tensiunilor coincid numai în jumătatea din dreapta a diametrului, adică valoarea cea mai mare a tensiunilor rezultante se obţine în B (punctul cel mai apropiat de pe secţiune faţă de axa arcului) şi se calculează astfel:
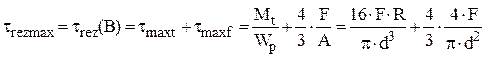
Ultima sumă poate fi scrisă sub o formă compactă, dacă se scoate în factor, în mod forţat, prima fracţie, iar relaţia calculului de rezistenţă va fi:
(5.4)
Arcurile obişnuite dau valori foarte mici pentru ultima fracţie din paranteză, având adică o pondere nesemnificativă a forfecării în calcule. Din acest motiv predimensionarea arcurilor se face neglijând paranteza din membrul stâng al condiţiei de rezistenţă (5.4), urmând ca la final, după stabilirea dimensiunii definitive a spirei, să se poată face o verificare a ei folosind relaţia exactă de mai sus.
Este important de subliniat că, spre deosebire de alte piese metalice folosite în ingineria mecanică, arcurile se fabrică din oţeluri aliate de mare rezistenţă, pentru care τa la forfecare (statică) are valori mari, cuprinse de obicei între 400 şi 800MPa, iar modulul de lunecare este G = 85GPa.
Un parametru important pentru exploatarea arcurilor este deformaţia lor axială sub acţiunea încărcărilor pe care trebuie să le suporte. Calculul ei se poate face, de exemplu, pe baza teoremei de conservare a energiei (a lui Clapeyron), care stabileşte că energia potenţială de deformare elastică U acumulată într-un arc, construit şi încărcat ca în figura 5.3, atunci când el se comprimă axial cu cantitatea δ, este egală în mărime cu lucrul mecanic elastic Le consumat pentru producerea respectivei deformaţii.
La studiul solicitărilor simple s-a arătat că acest lucru mecanic se calculează ca Le = (1/2)F·δ , în vreme ce pentru energia potenţială se ţine seama că ea este acumulată în mod preponderent prin torsiune, adică va fi calculată folosind relaţia de la solicitarea simplă respectivă:
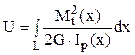
Se observă că, pentru arcul considerat, toate mărimile de sub integrala de mai sus sunt constante pe toată lungimea lui (care este egală cu lungimea unei spire 2πR înmulţită cu numărul total de spire n); folosind notaţiile făcute anterior, energia potenţială acumulată în arc se calculează astfel:
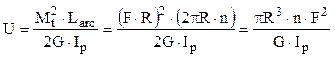
După egalarea ultimei fracţii cu expresia de mai sus a lucrului mecanic elastic, se obţine relaţia pentru calculul deformaţiei δ (numită şi „săgeata” arcului sub forţa F), sub forma:
(5.5)
Din fizica elementară se cunoaşte că, pentru orice element elastic, raportul dintre forţa F care îl încarcă şi deformaţia δ pe care i-o produce reprezintă o constantă a elementului respectiv, se notează de obicei cu litera k şi este una dintre cele mai importante caracteristici ale lui. Pe această bază se poate vorbi despre constanta arcului elicoidal studiat mai sus, calculată astfel:
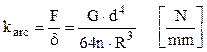(5.6)
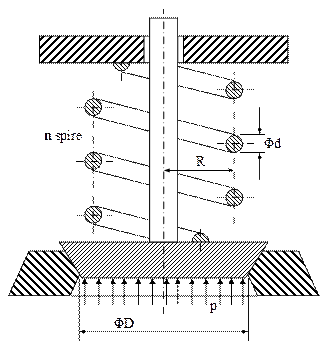 Fig. 5.5 |
Aplicaţie
5.3. Se consideră o supapă de siguranţă, cu diametrul nominal D=60mm, reglată să se deschidă când presiunea din instalaţie ajunge la p0=12atm.
Supapa este menţinută închisă cu un arc elicoidal cilindric (fig. 5.5), cu spire strânse şi raza R = 20mm; arcul este din oţel aliat, are modulul de elasticitate G=85GPa, rezistenţa τa=500MPa şi este comprimat, din momentul în care a fost montat, cu o deformaţie δ = 8mm.
Se cere să se dimensioneze arcul (adică să se stabilească parametrii lui d şi n), cunoscând că deschiderea maximă a supapei este de 3mm.
Rezolvare
Arcul trebuie dimensionat astfel încât să suporte, în condiţii de funcţionare stabilă şi reversibilă, distanţa de deschidere maximă a supapei, care corespunde comprimării lui cu 3mm în plus, faţă de deformaţia lui de regim notată cu δ. În acest sens, se calculează mai întâi forţa minimă de apăsare la care se deschide supapa, corespunzând presiunii p0 (la scrierea căreia se ţine seama de relaţia de transformare 1atm = 0,1MPa) care acţionează pe suprafaţa circulară, cu diametrul D, a supapei:
La această forţă comprimarea arcului este de 8mm şi aplicând regulile simple ale proporţionalităţii se calculează forţa maximă pe care trebuie să o suporte arcul, care va corespunde comprimării de 11mm:
Pentru stabilirea unei valori iniţiale a diametrului spirei se foloseşte condiţia de rezistenţă (5.4), cu neglijarea fracţiei din paranteză (adică a efectului produs de forfecare), din care rezultă următoarele:
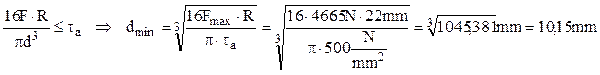
Se adoptă, pentru început, diametrul dad=10,2mm, pentru care condiţia riguroasă de rezistenţă (5.4) dă următorul calcul:
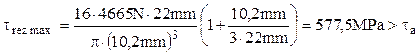
Acest rezultat arată că dimensiunea adoptată nu este suficient de mare şi arcul nu poate funcţiona corect; aceasta se întâmplă deoarece raportul d/R este destul de consistent, iar fracţia din paranteză (efectul produs în spire de solicitarea de forfecare) nu are o valoare neglijabilă, aşa cum s-a presupus când s-a făcut predimensionarea. Rezultă că diametrul spirei trebuie crescut în mod treptat, repetând operaţiile de verificare până când condiţia de rezistenţă este îndeplinită.
Efectuând calculele se obţine că arcul nu rezistă nici pentru valorile de 10,3mm, 10,5mm şi 10,6mm ale grosimii de spiră, pentru care tensiunea rezultantă maximă depăşeşte în continuare valoarea rezistenţei admisibile a oţelului. Abia adoptarea diametrului d=10,8mm duce la îndeplinirea condiţiei de rezistenţă:
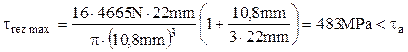
Pentru acest diametru trebuie stabilit numărul n de spire ale arcului; calculul se face folosind relaţia (5.5) a săgeţii, care poate fi aplicată pentru oricare dintre cele două niveluri ale forţei de apăsare, cu valorile corespunzătoare ale deformaţiei δ. De exemplu, pentru nivelul minim al forţei se obţine:
Prin urmare, arcul de supapă calculat în problemă trebuie făcut cu 4 spire, din sârmă cu diametrul de 10,8mm.
Observaţie: Spre deosebire de alte situaţii de proiectare, la calculul arcurilor elicoidale este nevoie de atenţie specială la adoptarea, prin rotunjire, atât a diametrului d, cât şi a numărului final de spire n; acest număr apare în relaţia pentru calculul săgeţii δ, deci dacă se adoptă pentru el o valoare mult mai mare decât cea de calcul, atunci se modifică tensionarea arcului, în spaţiul în care va fi montat şi trebuie refăcută dimensionarea lui.
C. Solicitări de tip (σ + σ)
Această categorie include cea mai largă varietate de solicitări compuse, inclusiv barele cu axe „plane”, cotite şi curbe, la care încărcările produc efecte numai în planul lor median longitudinal. Aceste tipuri de bare vor fi discutate în capitole ulterioare, iar prezentarea ce urmează se restrânge la efectele produse, asupra barelor drepte, de forţe care au orientări spaţiale distincte faţă de axele ataşate barelor.
C1. Cazul solicitărilor prin forţe cu direcţii înclinate în raport cu
axele principale ale barelor
Prin axe principale ataşate unei bare se înţeleg axa ei longitudinală, notată cu x în sistemul folosit în mod tipic în studiul rezistenţei materialelor, la care se adaugă axele principale centrale de inerţie, notate z (cea orizontală), respectiv y, ale secţiunilor transversale.
Pentru a se stabili ce tipuri de solicitări sunt produse de forţele cu orientări oarecare, se procedează la proiectarea fiecărei forţe pe direcţiile axelor menţionate, analizând eforturile secţionale nenule care apar în bară şi care pot fi de şase categorii:
a) proiecţia pe axa x a unei forţe produce întindere sau comprimare, cu tensiuni care se distribuie uniform pe secţiunile transversale;
b) proiecţiile pe y şi z tind să producă forfecare, pentru care tensiunile sunt, cu excepţia corpurilor masive, de tip bloc, puţin semnificative faţă de efectele date de celelalte solicitări;
c) dacă direcţia forţei nu întâlneşte axa barei, atunci proiecţia ei pe un plan perpendicular pe această axă va produce moment de răsucire; cazul în care se compun tensiuni σ şi τ a fost discutat anterior, astfel încât în acest paragraf va fi vorba numai despre forţe care întâlnesc axa x;
d) în fine, proiecţiile de pe axele y şi z produc şi momente de încovoiere, în raport cu axele z, respectiv y din secţiunile aflate la distanţă de punctele lor de aplicaţie.
Efectele din ultima categorie necesită o detaliere, cu privire la modul cum se calculează tensiunile pe care le produc. Pentru fiecare dintre momentele elementare axa de încovoiere coincide cu direcţia momentului, iar tensiunile sunt proporţionale cu distanţa până la această axă a fibrei în care se face calculul, în conformitate cu relaţia lui Navier:
(5.7)
Prin urmare, tensiunile sunt nule pe axa de încovoiere, care din acest motiv se numeşte axă neutră (notată de obicei A.N.) a secţiunii pentru solicitarea respectivă şi ating valorile maxime în punctele de pe secţiune aflate la distanţa cea mai mare faţă de axa neutră, adică la extremităţile ei (faţă de direcţia momentului care produce încovoierea). Se reaminteşte şi faptul că tensiunile de încovoiere au semne contrare, de o parte şi de alta a respectivei axe neutre a secţiunii.
În cele ce urmează vor fi prezentate cele trei cazuri tipice de încărcări care se încadrează în parametrii precizaţi mai sus. Nu va fi discutată în mod special aşa numita încovoiere „strâmbă”, la care pe o bară apar mai multe forţe ale căror direcţii nu sunt coplanare. Dacă aceste forţe se proiectează pe planele formate de axele principale ale barei, atunci se obţine o schemă de solicitare care se regăseşte între cele discutate aici.
C1.a. Forţe incluse într-un plan principal longitudinal al barei
Se înţelege prin plan longitudinal principal unul format de axele y sau z cu axa x a barei. Discuţia de faţă se poate baza pe oricare dintre ele, iar pentru a uşura înţelegerea ei s-a ales planul „vertical”, care conţine axa y. Încărcarea exterioară este dată de cel puţin o forţă, cuprinsă în acest plan şi înclinată sub un unghi α în raport cu axa x a barei.
Cel mult trei dintre componentele eforturilor vor fi prezente în secţiunile barei – forţa axială N(x), cea tăietoare Ty(x) şi momentul de încovoiere Miz(x). Din motivele precizate, importante în calcule sunt tensiunile axiale şi cele de încovoiere, care sunt de aceeaşi natură (tind să producă întindere sau comprimare în toate punctele secţiunilor transversale) şi la fel orientate (perpendiculare pe secţiuni), adică pot fi adunate algebric în oricare punct P(x, y, z) din volumul barei considerate. Se obţin astfel tensiunile rezultante, care trebuie să îndeplinească în fiecare punct condiţia de rezistenţă, scrisă sub forma:
(5.8)
 Fig. 5.6 |
Din relaţia (5.8) se observă că tensiunile rezultante nu variază în funcţie de coordonata z a punctelor secţiunii, adică sunt constante pe orice „fibră” orizontală a ei. Din acest motiv, graficul repartiţiei tensiunilor pe înălţimea unei secţiuni transversale poate fi prezentat în planul median longitudinal (x-y) (fig. 5.6). Pentru simplitate s-a ales cazul secţiunii dreptunghiulare, având avantajul simetriei faţă de axa de încovoiere, dar discuţia poate fi extinsă uşor la secţiunile fără simetrii.
Eforturile N(x) şi Miz(x) s-au luat cu semne considerate pozitive, de unde rezultă orientarea ca în figură a tensiunilor pe care le produc; în plus, axa y a fost dirijată în jos, pentru ca tensiunile pozitive de încovoiere să aibă loc în dreptul coordonatelor y pozitive. Se observă că sumarea algebrică a celor două categorii de tensiuni elementare conduce la translarea, cu mărimea tensiunilor axiale, a liniei pe care se plasează vârfurile tensiunilor de încovoiere. Aceasta face ca şi axa neutră (A.N.) să transleze şi să nu mai treacă prin centrul de greutate G al secţiunii barei. Ca urmare, cea mai mare tensiune rezultantă se înregistrează la acea extremitate a secţiunii unde cele două tensiuni elementare au acelaşi semn (adică sunt la fel orientate).
Pe de altă parte se ştie că, pentru secţiunile simetrice faţă de axa de încovoiere, tensiunile de la extremităţile secţiunii sunt egale şi de semn contrar, astfel încât relaţia (5.8) se va scrie la fel, în valori absolute, orice orientare ar avea tensiunile axiale. Prin urmare, semnul eforturilor N şi M nu are relevanţă în relaţia calculului de rezistenţă!
Observaţie: Axa neutră intersectează secţiunea numai dacă între tensiunile elementare există relaţia σax < σmax înc , în caz contrar toate valorile σrez(x) vor avea un singur semn şi aceeaşi orientare în orice punct al secţiunii.
Aplicaţie
5.4. Se consideră o bară dreaptă, aşezată pe un reazem simplu şi pe o articulaţie şi având secţiunea dreptunghiulară, pentru care lungimile laturilor se află în raport de 1:3. Pe bară acţionează o forţă concentrată, cuprinsă în planul ei median longitudinal şi plasată la distanţa de un sfert din lungimea barei, în raport cu reazemul simplu. Forţa este dirijată către acel reazem, are mărimea F = 2·104N şi direcţia înclinată la α = 60° faţă de orizontală.
Să se dimensioneze bara, cunoscând că are lungimea totală de 1,6m şi că este făcută din oţel cu σa = 160MPa.
Rezolvare
Schema de încărcare este prezentată mai jos, împreună cu diagramele de eforturi. Solicitarea compusă este de tipul descris în acest paragraf, întrucât componenta orizontală (F1 = F·cosα) a forţei produce întindere, pe distanţa dintre reazemul articulat şi punctul ei de aplicare, în vreme ce componenta ei verticală (F2 = 
F·sinα) produce încovoiere (ca solicitare semnificativă).
Solicitarea maximă are loc în secţiunea în care acţionează forţa F, iar valorile din acea secţiune ale eforturilor secţionale vor fi introduse în condiţia de rezistenţă (5.8).
Proiecţiile forţei F pe cele două axe principale din planul problemei vor fi înlocuite cu valorile lor:
Se mai face semnalarea că, atunci când se scrie tensiunea maximă de încovoiere, la numitorul fracţiei apare modulul de rezistenţă Wz al secţiunii calculate. În acest fel condiţia de rezistenţă se scrie sub forma:
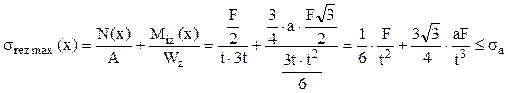
În condiţiile în care relaţia se foloseşte pentru dimensionarea unei bare, este preferabil să se înceapă cu un calcul preliminar, bazat doar pe al doilea termen al sumei, adică pe solicitarea de încovoiere, din care în acest caz rezultă următoarele:
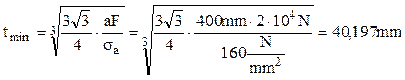
Dimensiunea adoptată, de exemplu la valoarea tad=42mm, trebuie verificată în condiţia completă de rezistenţă, astfel:
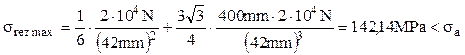
Condiţia este îndeplinită, deci secţiunea transversală a barei calculate poate să aibă dimensiunile (42×126)mm2.
C1.b. Forţe cuprinse în plane principale transversale ale barei
În aceste situaţii forţele exterioare nu vor avea componente axiale şi efectele de încovoiere, faţă de axele principale z şi y, vor fi singurele importante în calculul de rezistenţă al barei.
Solicitarea se numeşte încovoiere oblică (sau dublă) şi este clar că tensiunile elementare pot fi sumate algebric în fiecare punct al secţiunilor transversale, deoarece fiecare dintre ele tinde să producă întindere sau comprimare. Tensiunea rezultantă într-un punct oarecare P(x, y, z) va fi:
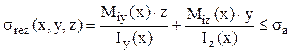(5.9)
Observaţii
Aplicaţie
5.5. Se consideră aceeaşi bară ca la aplicaţia 5.4, solicitată printr-o forţă de exact aceeaşi mărime, dar dirijată perpendicular pe axa longitudinală a barei şi înclinată faţă de celelalte două axe principale centrale ale acesteia, aşa cum se arată în figura 5.7 de mai jos. Să se dimensioneze bara, ştiind că înclinarea forţei este tot la unghiul α = 60° şi luând σa = 160MPa.
Rezolvare
Valorile reacţiunilor din reazeme apar în desen, ca şi diagrama momentelor de încovoiere produse în secţiunile transversale ale barei de forţa F, în planul longitudinal pe care îl formează cu axa x a barei. Alura diagramei va fi aceeaşi inclusiv în planele pe care componentele F1 şi F2 le formează cu axa x şi în care valorile momentelor se obţin făcând simpla înlocuire a lui F cu proiecţia ei din planul respectiv.
 Fig. 5.7 |
Este interesant de remarcat că bara tinde să fie îndoită atât în planul vertical din secţiunile transversale, adică în jurul axei y – de către forţa F1, cât şi în planul orizontal, în jurul axei z – de forţa F2. Relaţia generală (5.9), cu care se calculează valorile tensiunilor rezultante în punctele din secţiunea unde este aplicată forţa F (unde efortul de încovoiere este maxim) se scrie astfel:
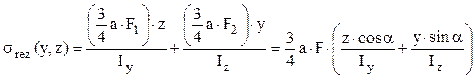
Relaţia calculului de rezistenţă se bazează pe cea mai mare dintre aceste valori, care poate fi stabilită, de exemplu, pe baza proprietăţilor axei neutre a unei secţiuni: dacă există o axă (A.N.) în problema de faţă, atunci valorile maxime ale relaţiei se vor obţine în punctele aflate la cea mai mare distanţă de (A.N.); chestiunea se clarifică observând că σrez = 0 implică egalitatea cu zero a ultimei paranteze din relaţia de mai sus, de unde rezultă că:
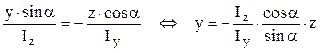
Ultima egalitate are forma unei ecuaţii de gradul I, reprezentând grafic o dreaptă ce trece (ca în fig. 5.7) prin originea axelor de coordonate şi prin cadranele trigonometrice I şi III. Este remarcabil că această dreaptă se va aşeza exact pe direcţia perpendiculară pe forţa F (direcţia efortului de încovoiere pe care această forţă îl produce), pentru secţiunile care au Iz = Iy, adică momentele principale centrale de inerţie egale ca valoare. Această proprietate se regăseşte la toate secţiunile cu 3 sau mai multe axe de simetrie (poligoanele regulate), pentru care rezultă că nu se va produce niciodată încovoiere oblică (îndoirea se produce la fel faţă de orice axă centrală)!
În problema de faţă, cele mai depărtate puncte de pe secţiune în raport cu (A.N.) sunt cele două colţuri ale dreptunghiului aflate aproape de direcţia forţei F, deci coordonatele (3t/2; t/2), respectiv (-3t/2; -t/2) trebuie înlocuite în relaţie pentru a calcula valorile σrez max.
Observaţie: Se poate urma şi o altă logică pentru a stabili punctele cele mai solicitate de pe secţiune. Sensurile axelor de coordonate au fost alese astfel încât tensiunile pozitive să se obţină de partea coordonatelor pozitive, pentru fiecare dintre momentele elementare de încovoiere (adică pentru fiecare din fracţiile din relaţia tensiunilor rezultante). Aşa cum apare schiţat pe figură, cele două categorii de tensiuni elementare au aceleaşi semne numai în punctele din cadranele II şi IV, deci doar acolo suma lor poate atinge maximul, în plus, valorile lor absolute sunt maxime simultan numai în colţurile secţiunii, deci colţurile din acele cadrane dau tensiunile σrez max.
Prin urmare, condiţia calculului de rezistenţă se va construi astfel:
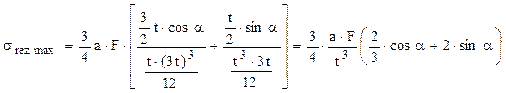
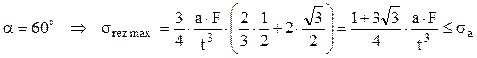
Dimensiunea necesară a secţiunii este:
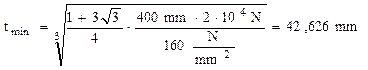
Aşadar, secţiunea dreptunghiulară cu dimensiunile (43×129)mm2 (foarte apropiate de cele de la aplicaţia precedentă) este suficientă pentru a prelua forţa F, în condiţiile date.
Un exerciţiu interesant se poate face urmărind ce se schimbă în calcule atunci când bara se sprijină pe latura mică a dreptunghiului, adică secţiunea ei dreptunghiulară se roteşte cu 90°, toate celelalte elemente ale problemei rămânând nemodificate. Practic, singurul efect este că, în relaţia tensiunilor rezultante, componentele F1 şi F2 fac schimb de locuri:
Tensiunile maxime se obţin tot în colţurile cele mai apropiate de direcţia forţei şi înlocuind coordonatele lor în relaţie se obţine:
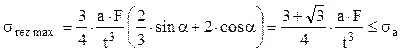
După înlocuirea valorilor numerice din problemă se obţine tmin = 38,963mm şi deci secţiunea barei trebuie să aibă măcar dimensiunile (39×117)mm2. Se poate spune că toate variantele analizate produc efecte apropiate ca intensitate în bara studiată.
Mai trebuie subliniat că, pentru a efectua calcule de dimensionare pe baza condiţiei (5.9), este necesar să fie cunoscută o relaţie (adică un raport) între dimensiunile secţiunii transversale a barei, ceea ce în problema de mai sus se preciza cu claritate în enunţ.
C2. Cazul solicitărilor prin forţe axiale care nu trec prin centrele de
greutate ale secţiunilor transversale
O astfel de solicitare se numeşte axială excentrică şi prezintă importanţă pentru multe situaţii practice, aşa cum se va arăta în continuare. Cel mai frecvent sunt întâlnite bare – cu secţiuni de forme diverse, aşezate vertical şi rezemate la bază –trebuind să susţină diverse încărcări, de mase importante, care le comprimă la capătul liber.
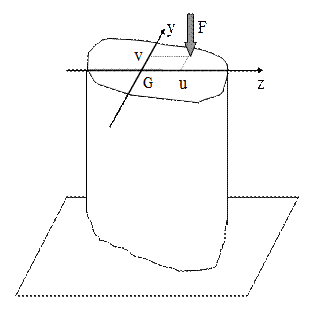 Fig. 5.8 |
De îndată ce sarcina nu este plasată în centrul de greutate G al secţiunii de capăt, ea va produce nu doar comprimare, ci şi încovoiere, în raport cu axa (axele) din secţiune faţă de care se află la distanţă.
În exemplul din figura alăturată, coordonatele (u, v) ale punctului în care se aplică forţa F reprezintă chiar distanţele la care se află forţa în raport cu cele două axe.
Se poate observa că, în orice punct din volumul barei vor exista simultan trei categorii de tensiuni, având următoarele relaţii de calcul:
- tensiunea produsă prin comprimare 
- tensiunea dată de încovoierea faţă de axa z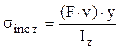 
- tensiunea dată de încovoierea faţă de axa y 
Deja aceste relaţii arată că tensiunea globală va depinde în mod exclusiv de coordonatele y şi z ale punctelor barei, adică nu are importanţă localizarea secţiunii transversale în care se face calculul. Pe această bază se va constata că înălţimea (sau lungimea) barei calculate nu influenţează calculele de rezistenţă pentru solicitările axiale excentrice!
Există totuşi, deci este important de avut în vedere, pericolul ca bara să-şi piardă stabilitatea longitudinală, astfel încât lungimea ei trebuie să fie suficient de mică pentru ca acest pericol să fie evitat.
Pe de altă parte, toate tensiunile elementare citate sunt de aceeaşi natură (tind să producă întindere sau comprimare) şi la fel orientate (perpendicular) faţă de secţiunile barei, deci pot fi adunate algebric în fiecare punct. Pentru ca aria A să poată fi extrasă ca factor comun, de la numitorul celor trei fracţii, se scriu momentele principale în funcţie de razele de inerţie care le corespund, încât relaţia tensiunii rezultante din punctul arbitrar P(z, y) al secţiunii va avea forma următoare:
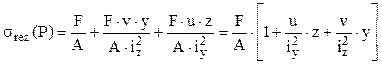(5.10)
Logica pentru găsirea tensiunilor maxime este la fel ca mai sus, adică are la bază existenţă axei neutre a secţiunii pentru această solicitare. Se observă că, orice formă ar avea secţiunea barei, locul geometric al punctelor ei în care σrez = 0 este dat de egalitatea cu zero a ultimei paranteze de mai sus, iar expresia care rezultă are chiar forma unei ecuaţii de gradul I (1+by+cz=0); ea va fi reprezentată grafic printr-o dreaptă, care este axa neutră căutată:
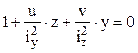(A.N.)
Această dreaptă nu trece prin originea axelor, astfel încât ea se trasează de obicei „prin tăieturi”, adică folosind punctele în care intersectează axele de coordonate; aceste puncte se obţin făcând pe rând, în ecuaţia dreptei, una dintre coordonate egală cu zero.
Odată trasată axa neutră, punctele aflate la distanţa cea mai mare faţă de ea vor fi cele mai solicitate de pe secţiune, iar coordonatele lor trebuie înlocuite în expresia (5.10) a tensiunilor rezultante pentru a scrie valoarea lor maximă; aceasta va reprezenta membrul stâng al condiţiei de rezistenţă pentru bara calculată.
Trebuie semnalat şi un alt caz, frecvent întâlnit, de solicitare axială excentrică, cel al barelor la care, din raţiuni diverse, este necesar să apară decupări transversale asimetrice pe anumite porţiuni din lungimea lor, aşa cum se va exemplifica în cea de-a doua aplicaţie de mai jos.
Aplicaţii
5.6. Se imaginează o bară verticală, rezemată ca în fig. 5.8, de lungime oarecare, destul de mică pentru a nu exista pericol de flambaj longitudinal. Secţiunea este dreptunghiulară, la fel pe toată lungimea. Nu sunt necesare ipoteze speciale privind proporţiile secţiunii, încât laturile ei se notează simplu, cu h şi b. Se cere să se stabilească relaţia calculului de rezistenţă pentru această bară, dacă este încărcată cu o forţă de comprimare aplicată în colţul dreptunghiului din cadranul unde ambele coordonate sunt pozitive.
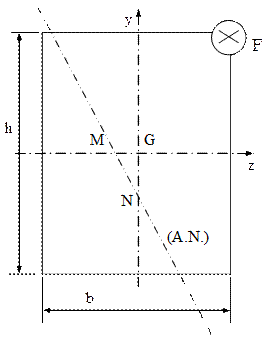 Fig. 5.9 |
Rezolvare
Este remarcabil că răspunsul la această problemă poate fi găsit fără ca gradul ei de generalitate să se restrângă în vreun fel, pentru că totul va fi calculat în litere, iar datele numerice nu sunt necesare.
Pentru început se precizează valorile coordonatelor punctului de pe secţiune în care acţionează forţa F: acestea sunt.
Pentru a nu deduce din nou termenii din relaţia (5.10) (ceea ce totuşi poate fi făcut în orice problemă, adică nu e deloc necesară memorarea relaţiei!), se scriu valorile mărimilor care o compun, astfel:
Cu aceste valori, ecuaţia axei neutre a secţiunii se scrie:
(A.N.)
Pentru a trasa această dreaptă pe desenul secţiunii, se stabilesc punctele ei de intersecţie cu axele de coordonate:
Prin aceste puncte se duce axa neutră şi se observă că punctul cel mai depărtat faţă de ea de pe secţiune este chiar cel în care se aplică forţa:
Concluzii. Problema sâmburelui central
Ultimul rezultat este valabil pentru orice secţiune dreptunghiulară cu forţa axială aplicată într-unul dintre colţurile sale. El exprimă ideea, extrem de interesantă, că abaterea forţei de la poziţia centrică duce la creşteri importante ale tensiunilor maxime din bară – în acest caz se obţin tensiuni de 7 ori mai mari decât cele produse de aceeaşi forţă aplicată în centrul de greutate al secţiunilor, adică pe direcţia axei longitudinale a barei!
Relaţia calculului de rezistenţă pentru bara analizată se va scrie:
Aplicarea excentrică a forţei face necesar un consum de material de 7 ori mai mare, sau aplicarea unei forţe de 7 ori mai mici, faţă de cazul standard de solicitare. Prin urmare, efectele excentricităţilor nu sunt de neglijat şi trebuie stabilite prin calcule riguroase, în orice situaţie practică de acest fel.
Pe de altă parte este necesar ca, dacă în faza de proiectare este întâlnită o astfel de solicitare, să se stabilească ce abateri faţă de axa barei sunt permise, la montarea sarcinilor ei de comprimare, pentru a nu i se pune în pericol funcţionarea stabilă şi reversibilă. De exemplu, în cazul unui stâlp de beton solicitat ca în problema de mai sus, este important să se evite apariţia în volumul său a unor tensiuni de întindere: acestea se vor produce de îndată ce axa neutră taie secţiunea stâlpului. Tensiunile din punctele aflate de partea forţei F, în raport cu (A.N.), au acelaşi semn cu F, adică cele situate dincolo de (A.N.) vor fi de întindere!
Definiţie: Se numeşte sâmbure central al secţiunii transversale a unei bare, locul geometric al punctelor ei în care poate fi aplicată o forţă axială astfel încât tensiunile de pe întreaga secţiune să aibă acelaşi semn cu forţa.
Acest loc geometric se găseşte scriind condiţiile matematice necesare pentru ca axa neutră a secţiunii, la solicitarea respectivă, să fie cel mult tangentă la secţiune, adică să aibă un singur punct de contact cu ea. Pentru secţiunile cu contururi curbilinii calculul poate fi destul de laborios, dar dacă este posibil să se scrie o ecuaţie pentru contur, atunci de obicei se găseşte tot o ecuaţie şi pentru conturul sâmburelui central (care de exemplu este un cerc, respectiv o elipsă, pentru secţiunile care au aceste forme).
În schimb, pentru secţiunile cu forme poligonale calculul se face simplu şi logic – există întotdeauna un număr finit de poziţii de tangenţă la secţiune pe care le poate ocupa axa neutră; se scriu ecuaţiile acelor drepte şi se identifică cu ecuaţia literală a (A.N.), de unde rezultă coordonatele punctului de aplicare a forţei ce corespunde fiecăreia dintre drepte.
Punctele astfel găsite reprezintă vârfurile unui poligon care coincide cu sâmburele central al secţiunii analizate. Trasarea laturilor acelui poligon se bazează pe următoarea regulă:
Teoremă: Atunci când axa neutră a unei secţiuni ocupă poziţii care au un punct comun (adică se roteşte în jurul acelui punct), forţa axială care produce solicitarea se aplică în puncte ale secţiunii care se află pe o aceeaşi dreaptă.
5.7. Să se traseze sâmburele central al unei secţiuni în formă de dreptunghi dintr-o bară solicitată în condiţiile din aplicaţia anterioară.
Rezolvare
Principala particularitate a acestei probleme constă în faptul că sunt de aflat nişte coordonate ale punctelor în care trebuie aplicată forţa F, adică se ştie secţiunea, dar (la momentul iniţial) nu se ştie nimic despre valorile notate mai sus prin u şi v.
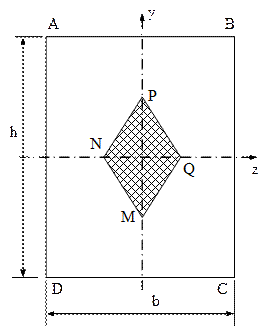 Fig. 5.10 |
Nici în acest caz nu sunt necesare valori numerice ale dimensiunilor, astfel încât concluziile vor fi valabile pentru orice secţiune cu această formă.
Se porneşte de la ecuaţia literală a axei neutre, având ca singură particularizare valorile razelor de inerţie date mai sus, cu care ecuaţia se scrie:
(A.N.)
Aşa cum s-a arătat, această dreaptă trebuie făcută să coincidă, succesiv, cu laturile secţiunii poligonale considerate.
Pentru a scrie condiţiile pentru care (A.N.) coincide cu latura AB, ecuaţia dreptei care trece prin aceste puncte trebuie adusă la forma ecuaţiei de mai sus a axei neutre:
Cele două ecuaţii vor reprezenta aceeaşi dreaptă dacă şi numai dacă vor avea aceleaşi valori ale coeficienţilor lui y şi z, adică:
S-a obţinut că, dacă forţa este aplicată în punctul M, marcat pe desenul de mai sus, atunci axa neutră trece prin punctele A şi B.
În mod analog se pun condiţiile de coincidenţă a axei neutre cu BC:
Dacă forţa este aplicată în punctul N, axa neutră trece prin colţurile B şi C ale secţiunii. Conform teoremei de mai sus, atunci când (A.N.) va ocupa o poziţie oarecare de tangenţă la secţiune în punctul B (adică se va roti în jurul acestui punct), forţa care îi corespunde va fi aplicată într-un punct de pe segmentul MN.
În mod analog, când axa neutră va ocupa poziţiile de tangenţă din punctul C, rotindu-se din poziţia BC în CD, punctul de aplicare a forţei se va afla pe segmentul NP (unde P este simetric lui M faţă de originea axelor de coodonate); rotirile în jurul lui D, respectiv A corespund aplicării forţei în puncte de pe segmentele PQ, respectiv QM (Q fiind simetric cu N).
Aşadar, pentru cazul de solicitare studiat, tensiunile rezultante au în toate punctele acelaşi semn cu forţa, pentru că axa neutră este doar tangentă la secţiune, dacă forţa axială este aplicată în punctele de pe conturul rombului MNPQ, care este sâmburele central al secţiunii dreptunghiulare. Când forţa este aplicată în interiorul rombului, axa neutră nu are nici un punct comun cu secţiunea, iar dacă forţa se aplică într-un punct exterior rombului, atunci axa neutră taie secţiunea în două părţi, în care tensiunile rezultante au semne contrare.
Există şi alte proprietăţi interesante ale axei neutre a unei secţiuni oarecare, dintre care unele derivă direct din cele prezentate până aici:
a) axa neutră trece întotdeauna prin cadranul opus celui unde acţionează forţa axială;
b) în cazurile în care greutatea proprie a barei este neglijabilă faţă de forţa exterioară, poziţia axei neutre nu este influenţată de mărimea forţei, ci numai de coordonatele punctului în care aceasta este aplicată;
c) dacă punctul de aplicare a forţei se deplasează către centrul de greutate al secţiunii, atunci axa neutră se îndepărtează de acest centru (şi reciproc);
d) atunci când forţa se deplasează pe o dreaptă care trece prin centrul de greutate, axa neutră translează paralel cu ea însăşi;
e) dacă deplasarea forţei se face chiar pe una dintre axele principale centrale ale secţiunii, atunci axa neutră se mişcă paralel cu cealaltă axă p.c.;
f) din relaţia (5.10) se observă că valoarea tensiunii rezultante nu se schimbă dacă punctul unde se face calculul se mută în punctul de aplicare a forţei, iar forţa se aşează în punctul iniţial de calcul.
5.8. Se consideră o tijă cu secţiunea de formă pătrată cu latura a, solicitată la tracţiune cu forţele F.
a. Să se stabilească modul cum se modifică tensiunea din tijă, atunci când pe o porţiune din lungimea ei secţiunea este micşorată prin decupări simetrice de adâncime a/4.
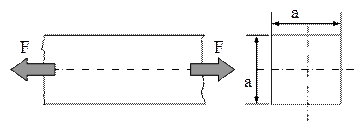  Fig. 5.11 |
b. Să se observe consecinţele produse de o decupare asimetrică a secţiunii, tot pe adâncimea a/4.
Rezolvare
a. În figura alăturată este schiţată solicitarea barei în starea iniţială, respectiv după prelucrarea celor două decupări simetrice.
În ambele cazuri forţele sunt aplicate pe direcţia axei longitudinale a tijei şi tensiunile vor fi numai de întindere.
Pentru tija fără decupări se produc tensiuni de aceeaşi valoare în orice punct din volumul barei:
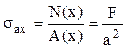
Tija cu decupări are tensiunile maxime în zona slăbită:
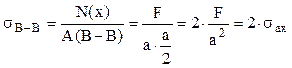
Secţiunea din zona decupărilor este ca mărime jumătate din cea iniţială, astfel încât tensiunile maxime sunt duble faţă de cele din zona nedecupată.
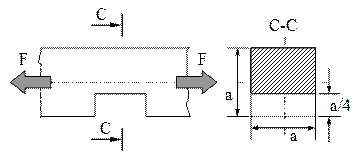 Fig. 5.12 |
b. Dacă secţiunea tijei este micşorată nesimetric (ca în fig. 5.12), tensiunile maxime se produc tot în zona slăbită, dar forţele F sunt poziţionate decalat faţă de centrul de greutate al secţiunii nete.
Ca urmare, calculul în acea zonă trebuie făcut după metoda de la solicitările axiale excentrice, folosind parametrii prezentaţi, pe o imagine mărită a secţiunii slăbite, în figura 5.13.
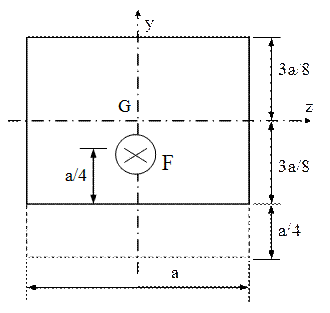 Fig. 5.12 |
Pe de o parte, tensiunile date de solicitarea axială propriu-zisă vor fi calculate astfel:
Tensiunile de încovoiere sunt cauzate de decalarea forţei F, cu distanţa a/8, faţă de centrul de greutate G al ariei slăbite, iar valorile lor maxime sunt:
După simplificarea valorilor numerice din ultima fracţie se ajunge la exact acelaşi rezultat ca la tensiunile axiale, iar tensiunile rezultante maxime, care se obţin la limita de jos a secţiunii slăbite (unde cele două categorii de tensiuni elementare sunt orientate la fel) se vor calcula astfel:
