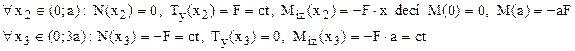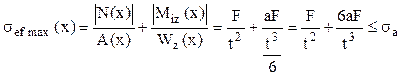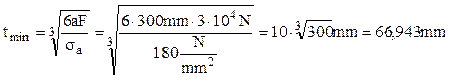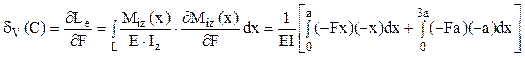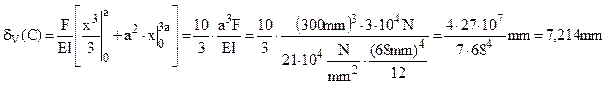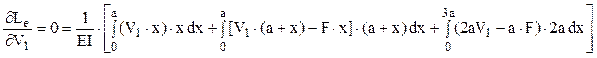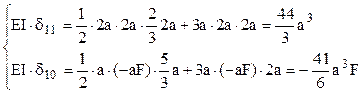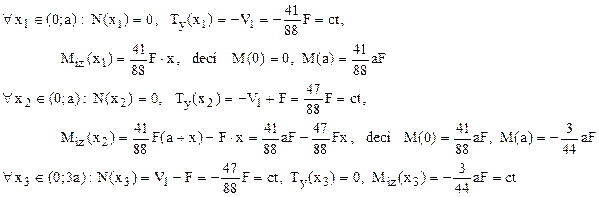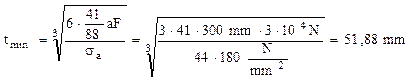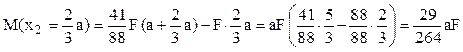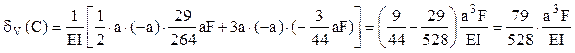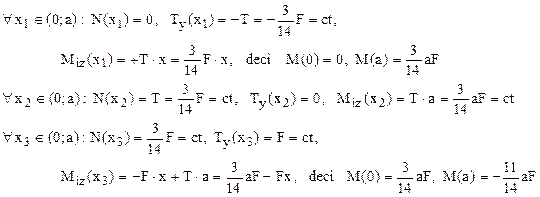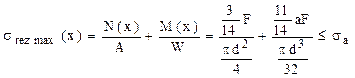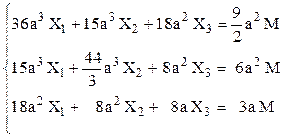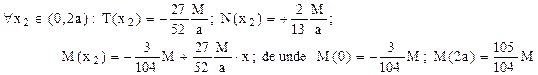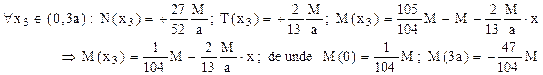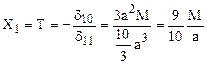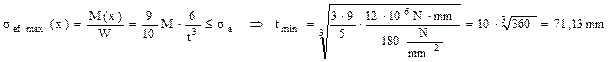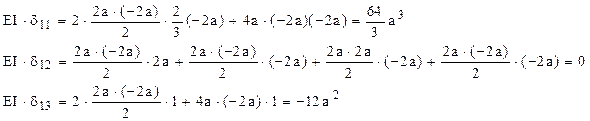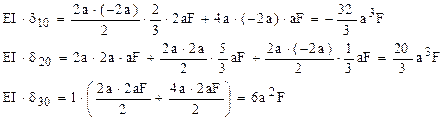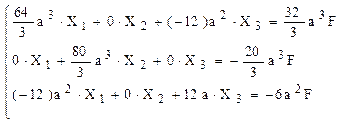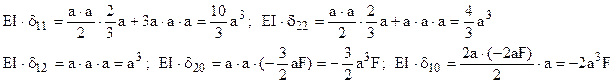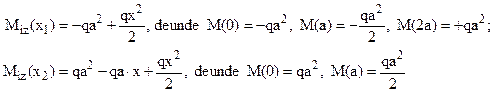Prezentul capitol se referă la barele ale căror axe nu mai sunt drepte, pe toată lungimea lor, ci sunt formate din segmente drepte, îmbinate rigid în noduri, dar având axele plasate pe direcţii diferite; dacă o astfel de bară este numită plană înseamnă că aceste direcţii sunt toate coplanare, cuprinse deci în ceea ce va constitui planul median longitudinal al barei.
În cele ce urmează sunt discutate numai bare ale căror solicitări îşi produc efectele în mod exclusiv în interiorul acestui plan, de unde rezultă că în orice punct al barelor vor exista cel mult trei categorii de eforturi secţionale – forţele axiale şi tăietoare dirijate pe axele planului, respectiv momentul de încovoiere având ca vector direcţia perpendiculară pe plan.

Particularităţi de calcul

Specificul barelor cotite este determinat chiar de schimbarea direcţiei axei lor longitudinale, în punctele de graniţă dintre segmentele din care sunt alcătuite. De o parte şi de alta faţă de aceste puncte eforturile secţionale vor avea expresii diferite, adică se vor delimita regiuni diferite ale barei.
În cazurile, foarte frecvente, în care două segmente învecinate sunt reciproc perpendiculare, trebuie observat că între cele două regiuni astfel apărute au loc permutări ale efectelor date de încărcările exterioare de tip forţă: astfel, forţele de tip axial de pe prima regiune devin tăietoare pe cea de-a doua, fiind desigur adevărată şi afirmaţia reciprocă. Pe acestă bază diagramele N(x) şi T(x) vor avea întotdeauna salturi, care nu sunt provocate de prezenţa unor forţe concentrate exterioare, în punctele de graniţă dintre segmentele de direcţii diferite.
În schimb, deoarece momentele secţionale se calculează mereu faţă de un punct (centrul de greutate al secţiunii abordate), diagramele de momente vor fi continue pe toată lungimea lor, în toate situaţiile! Aceasta desigur nu exclude prezenţa salturilor date de momentele concentrate exterioare, dar care sunt de fapt tot o probă a continuităţii diagramelor.
Pe de altă parte se reaminteşte că efectele produse de forţele tăietoare sunt puţin semnificative, pentru barele care au înălţimea secţiunilor transversale mult mai mică decât lungimea segmentelor lor, astfel încât calculul de rezistenţă se face ca la solicitările de tip „σ + σ”, din condiţia:

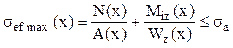                        (6.1)
Discuţiile asupra acestei relaţii rămân valabile, aşa cum au fost făcute la capitolul despre solicitările compuse, iar calculul se face de obicei în secţiunea în care momentul de încovoiere are valoarea cea mai mare de pe bară; dacă există o altă secţiune în care forţa axială atinge maximul, iar momentul are şi el o valoare semnificativă, este indicat ca rezultatul obţinut mai sus să fie verificat, cu aceeaşi relaţie, în secţiunea respectivă.



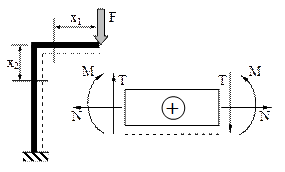
Fig. 6.1

            O precizare suplimentară trebuie făcută în legătură cu adoptarea convenţiilor de semne, pentru barele cotite, la calculul expresiilor eforturilor secţionale: convenţiile de la barele drepte se păstrează în totalitate (fig. 6.1), iar pentru ca semnele momentelor de încovoiere să păstreze aceeaşi regulă pe toată lungimea barei se duce o fibră punctată, alăturată axei ei.
Păstrarea poziţiei „interioare” a acestei fibre faţă de axa longitudinală a barei şi pe toată lungimea ei este esenţială, iar regula de semne se defineşte luând-o ca reper. De obicei sunt considerate pozitive acele momente care tind să solicite la tracţiune fibra punctată din secţiunea de calcul.

Grade de nedeterminare

Necunoscutele static nedeterminate pot să apară, în cazul barelor cotite, atât ca reacţiuni în reazeme, mai numeroase decât expresiile matematice din care pot fi calculate, cât şi ca eforturi secţionale, pentru construcţiile care conţin segmente grupate sub formă de contururi închise.

a) Cazul nedeterminărilor exterioare
La fel ca la barele drepte, aceste necunoscute sunt forţe şi/sau momente de legătură, adică reacţiuni acţionând în reazemele construcţiei analizate. Dacă se notează cu N numărul total al acestor reacţiuni şi cu E numărul de ecuaţii de echilibru semnificative care pot fi scrise în problema considerată, rezultă că gradul nedeterminării exterioare a construcţiei va fi   n = N – E .
Dacă se admite că, de regulă, barele cotite se sprijină pe cel mult două reazeme şi presupunând că ambele sunt încastrări (adică introduc fiecare câte trei reacţiuni), cunoscând că în problemele plane se pot scrie cel mult 3 ecuaţii de echilibru rezultă gradul maxim de nedeterminare, pentru barele cotite care se încadrează în aceste descrieri:   nmax = 6 – 3 = 3

b) Cazul nedeterminărilor interioare
Orice contur închis, format din segmente drepte sau curbe de bare, introduce pentru construcţia din care face parte un număr de 3 (trei) necunoscute interioare static nedeterminate. Explicaţia constă în faptul că un astfel de contur nu are, în starea lui naturală, un punct de început, sau de sfârşit, din care să se iniţieze studiul eforturilor sale secţionale, de unde necesitatea de a decupa imaginar conturul, într-o secţiune transversală oarecare.
Dacă se imaginează o bară reală, pe care încărcările exterioare tind să o tensioneze în fiecare punct al ei, se înţelege că orice secţionare a barei va avea tendinţa să elibereze tensiunile din materialul barei, făcând practic să dispară solicitările pe care ea le suporta. Pentru ca această eliberare (relaxare) să nu aibă loc şi starea de solicitare dinainte de secţionare să fie menţinută, pe fiecare faţă a tăieturii făcute, în centrul ei de greutate (adică pe axa barei) trebuie aplicate (fig. 6.2) câte 3 eforturi necunoscute (un moment M, care produce rotire în planul problemei şi două forţe N şi T, având direcţiile tangentei, respectiv normalei la axa barei din acea tăietură).


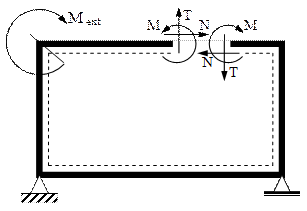
Fig. 6.2

            Cele şase eforturi astfel introduse, câte 3 pe fiecare faţă a secţiunii imaginare, sunt egale şi opuse în perechi, astfel că în fapt în secţiunile barei apar 3 necunoscute suplimentare, ale căror valori nu pot fi găsite din ecuaţiile de echilibru (la care nu participă, întrucât sunt încărcări interioare), deci se încadrează între necunoscutele static nedeterminate ale problemei.
Foarte importantă este semnalarea că aceste mărimi necunoscute reprezintă chiar valorile eforturilor secţionale respective, din secţiunea imaginară făcută, ceea ce înseamnă că se vor regăsi (ca mărime şi sens de acţiune) pe diagramele de eforturi ale barei, în dreptul acelei secţiuni.
Valorile lor se găsesc prin calcule similare celor de la barele drepte, bazate pe teorema din teoria elasticităţii (a lui Menabrea) conform căreia necunoscutele static nedeterminate au astfel de mărimi încât conduc la minimizarea consumului de lucru mecanic elastic de deformare pentru construcţia considerată, sub încărcările pe care le suportă.
Rezultă că derivatele parţiale, în raport cu oricare dintre aceste necunoscute, ale energiei de deformare elastică trebuie să fie nule, astfel încât şi pentru aceste categorii de construcţii se pot folosi, la rezolvarea nedeterminărilor, metodele aplicate la calculul barelor drepte, precum teoremele lui Castigliano sau metoda eforturilor.

Efectele produse de simetrii şi antisimetrii

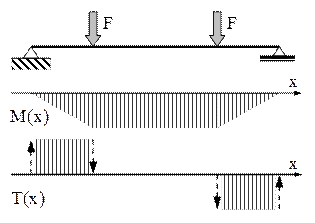
Fig. 6.3

Din studiul solicitărilor simple se cunoaşte că (aşa cum se exemplifică în fig. 6.3), dacă o construcţie oarecare este simetrică, iar solicitările ei exterioare acţionează de asemenea simetric, atunci diagramele de eforturi N(x) şi M(x) vor fi şi ele simetrice, în vreme ce diagrama T(x) va fi antisimetrică. În mod similar, dacă încărcările acţionează antisimetric, atunci diagramele N şi M sunt antisimetrice, iar diagrama T este simetrică.
Pe de altă parte, este interesant de observat că diagramele care sunt antisimetrice trec întotdeauna prin zero pe axa de simetrie a construcţiei, ceea ce înseamnă că, dacă o bară cotită care conţine contururi închise poate fi încadrată în una dintre situaţiile de mai sus, atunci secţionarea ei imaginară este potrivit să se facă în puncte aflate pe una dintre axele de simetrie ale construcţiei.
Ţinând seama de observaţiile făcute mai sus, se va obţine că într-o astfel de secţiune efortul necunoscut T va fi nul, dacă încărcările sunt simetrice, sau eforturile N şi M vor fi nule, dacă solicitările barei sunt antisimetrice. Pe această cale se ajunge pentru barele cotite la micşorarea gradului de nedeterminare, aşa cum se va exemplifica în unele dintre aplicaţiile care urmează.

Calculul deplasărilor la sistemele static nedeterminate

Pentru sistemele elastice din această categorie se ştie că, după ce au fost calculate valorile necunoscutelor static nedeterminate Xi, sistemul iniţial cu încărcările lui devine echivalent cu sistemul său de bază pe care se aplică atât încărcările iniţiale, cât şi necunoscutele respective Xi .
În acest fel se poate înţelege că diagramele reale de eforturi vor fi aceleaşi, pentru cele două sisteme, iar la aplicarea teoremei Mohr-Maxwell starea fictivă de încărcare poate fi construită pe sistemul de bază, făcând ca această stare de solicitare să fie static determinată.
Prin urmare la calculul deplasării unei secţiuni oarecare dintr-un astfel de sistem, pe o direcţie oarecare, se parcurg următoarele etape:

Aplicaţii


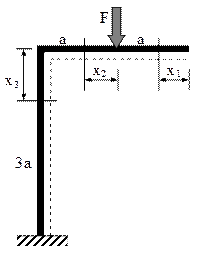
Fig. 6.4

6.1. Să se dimensioneze bara cotită figurată alăturat, ştiind că are secţiunile transversale de formă pătrată, constantă pe toată lungimea şi că este din oţel, cu E=21×104 şi σa=180 [MPa]. Se mai cunosc F=3×104 N şi a=0,3m. Pentru bara astfel calculată să se stabilească deplasarea pe verticală a punctului în care este aplicată forţa concentrată F.

Rezolvare

Se observă că regiunea (x1), aflată la capătul liber al barei, înaintea punctului unde se aplică forţa este nesolicitată, adică toate eforturile secţionale de pe acea regiune sunt nule.
Pe de altă parte se ştie că, dacă o bară are un singur reazem încastrat, se poate evita apariţia în calcule a reacţiunilor din acel reazem, dacă pe toate regiunile se iau în considerare încărcările din partea dinspre capătul liber (adică dinspre forţa F, în acest caz). Rezultă că nu este nevoie, în cazul de faţă, de calculul reacţiunilor.
Folosind împărţirea în regiuni din figura 6.4, eforturile secţionale de pe cele două regiuni semnificative se calculează astfel:



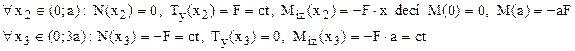
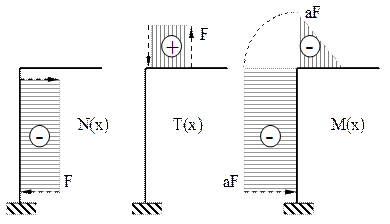
Fig. 6.5

Folosind aceste rezultate, diagramele de eforturi se trasează ca în figura alăturată, care arată că solicitarea periculoasă are loc în toate secţiunile de pe segmentul vertical al barei. Prin urmare, relaţia calculului de rezistenţă se va scrie astfel:

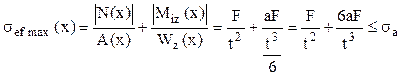
Ca şi în alte situaţii de acest fel, pentru dimensionarea secţiunii pe baza unei asemenea relaţii se face mai întâi un calcul aproximativ, numai pe baza solicitării de încovoiere, adică se scrie:

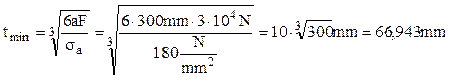
Mărind puţin dimensiunea astfel obţinută, de exemplu alegând t=68mm, se face un calcul de verificare din condiţia exactă:

Această valoare se plasează foarte bine, în preajma rezistenţei admisibile a materialului barei şi este potrivită ca rezultat al calculelor de proiectare.
Observaţii

Deplasarea pe verticală a punctului (notat în continuare cu C) în care acţionează forţa F (care are chiar direcţie verticală) se poate calcula direct, pe baza expresiilor de mai sus ale eforturilor secţionale, aplicând prima teoremă a lui Castigliano.
Trebuie precizat că, deoarece energia potenţială de deformare elastică este acumulată în bară în mod preponderent datorită solicitării de încovoiere (încât efectele solicitărilor axiale sunt practic neglijabile), aplicarea teoremelor energetice la barele plane cotite şi curbe se referă exclusiv la aceasta. Prin urmare, deplasarea cerută se calculează astfel:


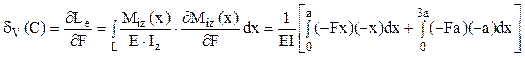
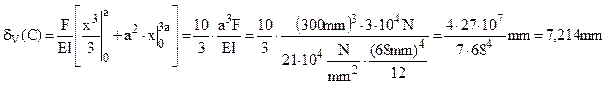
Dacă se preferă la calculul deplasării aplicarea teoremei Mohr-Maxwell, se observă, pe de o parte (fig. 6.6), că expresiile eforturilor m(x) din starea de încărcare fictivă coincid cu derivatele parţiale în raport cu F de pe cele două regiuni, calculate atunci când s-a folosit teorema lui Castigliano.


Fig. 6.6

   Prin urmare şi expresiile şi rezultatul calculului se vor obţine întru totul la fel ca mai sus.
Pe de altă parte trebuie remarcat că este foarte uşor să se traseze diagrama de momente din starea fictivă, pentru că graficele vor fi asemenea celor din diagrama reală, faţă de care trebuie făcută împărţirea tuturor valorilor la F!
Rezultă că se poate folosi fără dificultăţi metoda grafică de înmulţire a diagramelor (a lui Vereşceaghin), descrisă şi aplicată la studiul solicitărilor simple; folosind acest algoritm de calcul deplasarea pe verticală din punctul C va fi:


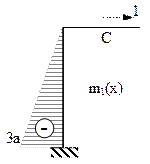
Fig. 6.7

Desigur că s-a ajuns la acelaşi rezultat ca mai sus, dar pe o cale care probabil este mult mai simplă şi sigur este mai rapidă decât metodele analitice. Nu este de neglijat constatarea că rezultatul este pozitiv aratând că punctul C se deplasează în sensul forţei (în jos).
Dacă trebuie să se calculeze deplasarea totală din C, atunci una dintre metodele de mai sus (fig. 6.7) se va folosi în legătură cu componenta ei orizontală δH(C).
De exemplu, teorema Mohr-Maxwell implică diagrama fictivă din figură, iar înmulţirea ei (prin metoda grafică a lui Vereşceaghin) cu diagrama reală de momente duce la următorul calcul:

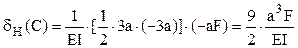
Deplasarea totală a secţiunii din C va fi rezultanta celor două deplasări componente:

Înlocuind cu datele numerice din problemă se ajunge la o deplasare totală de 12,118 mm (având direcţie oblică şi sensul către dreapta jos), care este cu totul acceptabilă pentru dimensiunile de gabarit ale barei considerate şi poate fi asumată ca deformaţie din domeniul de elasticitate al oţelului din care bara este realizată.


Fig. 6.8

6.2. Se propune să se analizeze modul în care se schimbă solicitarea barei cotite din aplicaţia precedentă, dacă este aşezată pe un reazem suplimentar, de tip simplu, plasat în capătul ei liber (fig. 6.8).

Rezolvare
Principala modificare este dată de apariţia unei noi reacţiuni verticale (V1), prin care problema devine static nedeterminată. Etapa în care se calculează reacţiunile nu mai poate fi neglijată, iar proiecţiile de forţe pe orizontală se reduc la reacţiunea H2, care deci va fi nulă.
Rămân necunoscute trei reacţiuni, din numai două ecuaţii de echilibru seminificative:

Observând că împărţirea în regiuni s-a făcut exact la fel ca la problema anterioară, se alege forţa V1 ca necunoscută de lucru şi se scriu eforturile secţionale de încovoiere în funcţie de ea:

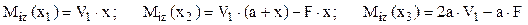
Aplicarea teoremei lui Castigliano în raport cu reacţiunea V1 se scrie:


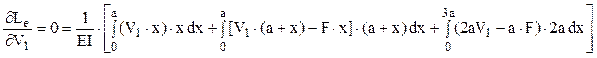
După efectuarea operaţiilor matematice din membrul drept al acestei ecuaţii, se găseşte că reacţiunea are valoarea   V1 = (41/88)F.


Fig. 6.9

   Pentru a şti dacă rezultatul este corect, se poate rezolva nedeterminarea pe o altă cale, precum metoda eforturilor: reazemul simplu va fi cel îndepărtat (fig. 6.9), pentru a obţine sistemul de bază pe care se construiesc cele două stări de încărcare imaginare.
Pe baza diagramelor, cei doi coeficienţi ceruţi de metodă se calculează astfel:

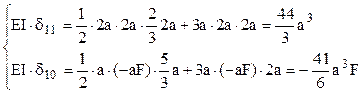
Cu aceste valori se calculează forţa necunoscută, din singura ecuaţie a metodei eforturilor:

Cele două metode aplicate au condus la acelaşi rezultat, care va fi folosit în continuare la stabilirea expresiilor eforturilor secţionale, în vederea trasării diagramelor de eforturi care corespund barei reale.
Folosind împărţirea în regiuni şi celelalte notaţii din figura 6.8, se ajunge la următoarele calcule:

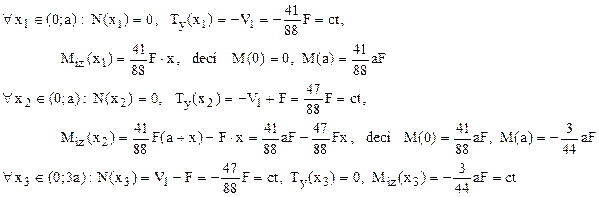
Analizând aceste rezultate şi diagramele reprezentate în figura 6.10 se poate constata că introducerea reazemului suplimentar conduce la uniformizarea solicitării pe lungimea barei cotite şi la înjumătăţirea valorilor eforturilor secţionale de tip forţă.



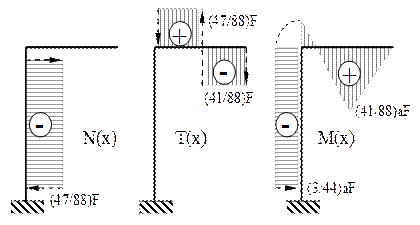
Fig. 6.10

   Cea mai importantă consecinţă este însă micşorarea, cu peste 50%, a efortului maxim de încovoiere, care nu se mai produce pe segmentul vertical al barei, ci chiar în secţiunea în care acţionează forţa concentrată F.
Prin urmare, faptul că problema a devenit static nedeterminată a dus la anumite complicări ale calculelor, dar scăderea solicitării maxime face posibile economii importante de material. Pentru a le evalua, trebuie făcut calculul de rezistenţă pentru noua variantă de rezemare a barei.
Este interesant de observat că în secţiunea periculoasă efortul axial este nul, deci dimensionarea barei cotite se va face numai pe baza solicitării de încovoiere, astfel:

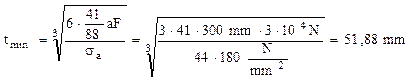
Secţiunea pătrată cu latura de 52mm este suficientă pentru ca bara să suporte în condiţii bune solicitarea. Dacă se calculează micşorarea de arie, faţă de secţiunea cu latura de 68mm din prima variantă, se obţine că economia de material (deci şi micşorarea greutăţii barei!) este de 41,5%.
Pentru a se calcula deplasarea pe verticală a secţiunii unde acţionează forţa F, s-a arătat că trebuie înmulţită diagrama reală M(x) a barei cu diagrama stării fictive (cu forţă unitară în punctul de calcul) de pe sistemul de bază; acesta coincide cu bara static determinată iniţială, deci starea fictivă va fi exact cea din figura 6.6 de mai sus.
Calculul pe cale grafică implică un singur aspect mai dificil, pe regiunea x2, unde trebuie calculată valoarea M(x) care corespunde centrului de greutate al triunghiului dreptunghic din diagrama m(x) de pe segmentul orizontal al barei:

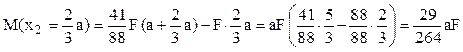
Folosind acest rezultat şi alegând să înmulţim, pe ambele regiuni semnificative ale graficelor considerate, aria diagramei m(x) cu valoarea de pe M(x), din dreptul centrului ei de greutate, se obţine:

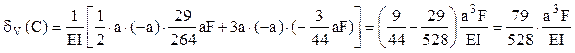
Acest rezultat arată că secţiunea punctului C se deplasează tot în jos, dar pe o distanţă foarte mică – de 22 de ori mai mică faţă de deplasarea din cazul solicitării static determinate; se poate afirma că introducerea reazemului suplimentar produce şi rigidizarea barei cotite analizate.



Fig. 6.11

6.3. Să se dimensioneze bara cotită construită şi solicitată ca în figura 6.11, ştiind că are secţiunile transversale de formă circulară plină, constantă pe toată lungimea şi că este din oţel, cu E=21×104 şi σa=160 [MPa]. Se mai cunosc F=2×104 N şi a=0,2m.

Rezolvare



Fig. 6.12

Datorită celor două reazeme încastrate (care introduc fiecare câte trei reacţiuni), problema este triplu static nedeterminată exterior.
Pe de altă parte, construcţia este simetrică, solicitată antisimetric, deci prin secţionarea ei imaginară pe axa de simetrie se va obţine micşorarea gradului de nedeterminare: diagramele eforturilor N(x) şi M(x) fiind antisimetrice, se deduce că necunoscutele care le corespund vor fi nule, în respectiva tăietură, iar singura necunoscută static nedeterminată rămasă va fi forţa tăietoare T.
Pe această bază este comod ca studiul să se facă pe o jumătate din construcţia iniţială (fig. 6.12), iar nedeterminarea se rezolvă simplu şi rapid cu metoda eforturilor.


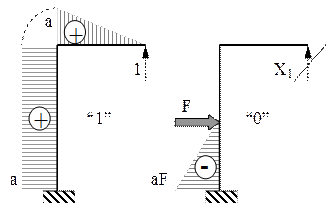
Fig. 6.13

   Sistemul de bază şi cele două stări fictive se construiesc ca în figura alăturată, pe care se observă uşurinţa cu care se pot trasa diagramele acestor stări de încărcare, practic fără să fie nevoie de expresiile eforturilor.
Pe de altă parte diagramele sunt liniare pe toate regiunile, deci coeficienţii δij se obţin după regula lui Vereşceaghin:

Din ecuaţia metodei eforturilor se calculează forţa necumoscută:

Introducând această valoare pe schema de solicitare din figura 6.12, se pot calcula expresiile eforturilor secţionale de pe jumătatea din stânga a barei, în cazul solicitării ei reale:


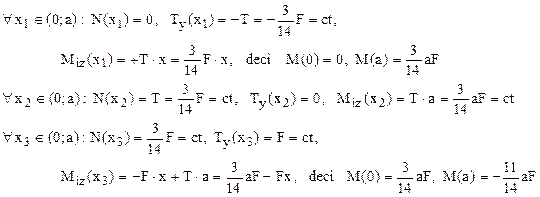
Diagramele de eforturi se trasează mai întâi pentru partea stângă a barei, apoi se prelungesc, în partea ei dreaptă, prin simetrie – pentru forţa tăietoare T(x), respectiv prin antisimetrie – pentru celelalte două diagrame (fig. 6.14).
Solicitarea periculoasă are loc în secţiunile din încastrări şi ţinând seama că secţiunile transversale sunt circulare pline, condiţia calculului de rezistenţă se va scrie astfel:



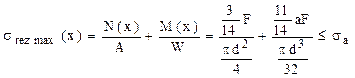
Fig. 6.14

Procedând la fel ca la o aplicaţie anterioară, se face o predimensionare a barei, numai din solicitarea de încovoiere:

Se măreşte puţin acest diametru, de exemplu la valoarea de 60mm şi se face verificarea condiţiei exacte de rezistenţă:


Prin urmare, tensiunea maximă din bară nu depăşeşte rezistenţa admisibilă a materialului ei, iar diametrul secţiunilor ei poate avea valoarea d = 60mm.

6.4. Să se dimensioneze bara cotită schiţată în figura 6.15, ştiind că are secţiunile de formă pătrată, aceeaşi pe toată lungimea şi că este din oţel de caracteristici E=21×104 şi σa=180 [MPa]. Se mai cunosc parametrii M=12kNm şi a=0,2m.

Rezolvare
Datorită celor două reazeme încastrate, problema este tot triplu static nedeterminată exterior; în schimb, deşi construcţia are o axă verticală de simetrie, solicitarea este nesimetrică, încât nu se pot face simplificări în calculele presupuse de rezolvarea nedeterminărilor.



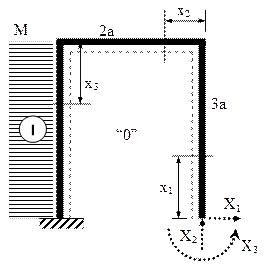
Fig. 6.16


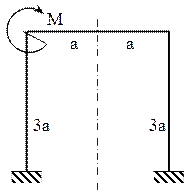
Fig. 6.15

   Sistemul de bază se obţine în modul cel mai direct îndepărtând imaginar una dintre încastrări, cum se arată în figura alăturată, în care se prezintă inclusiv cele trei necunoscute de lucru şi regiunile în care bara este divizată; este schiţată şi diagrama de momente a stării „0” de solicitare, cu sistemul de bază având ca singură încărcare momentul exterior M de pe bara reală.
Toate stările fictive vor avea diagrame de tip liniar (prezentate mai jos, în figura 6.17), astfel încât coeficienţii δij din ecuaţiile metodei eforturilor se pot calcula prin înmulţirea grafică a diagramelor, iar expresiile analitice ale eforturilor respective nu mai este necesar să fie scrise.
Cele trei ecuaţii ale metodei vor conţine 6 coeficienţi, ale căror valori sunt stabilite în cele ce urmează.



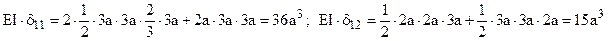
Fig. 6.17



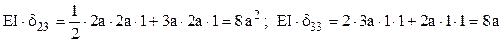
Introducând aceste rezultate în sistemul de ecuaţii ale metodei eforturilor şi simplificând toţi termenii prin EI, se ajunge la:

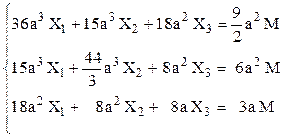
Prin rezolvarea acestui sistem de ecuaţii se obţin următoarele valori ale celor trei eforturi (reacţiuni) necunoscute:

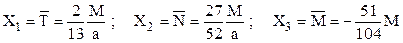
Folosind aceste rezultate în schema de solicitare din figura 6.16, se scriu următoarele expresii ale eforturilor secţionale de pe bara reală:


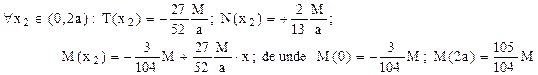
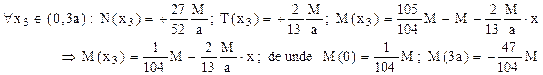
Aceste evoluţii arată că solicitarea periculoasă a barei se produce la capătul din stânga al segmentului orizontal de pe bara cotită considerată, chiar înaintea punctului în care este aplicat momentul concentrat M. Valoarea din acel punct a efortului de încovoiere coincide practic cu M (cu o eroare mai mică de 1/100), iar efortul axial din aceeaşi secţiune are valoare neglijabilă, încât se poate admite ca dimensionarea să fie făcută luând în considerare numai solicitarea de încovoiere:

Pe baza considerentelor de mai sus se adoptă secţiunea pătrată având laturile egale cu t=60mm.



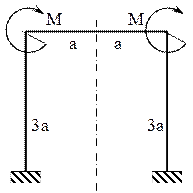
Fig. 6.18

6.5. Să se analizeze cum se modifică solicitarea barei cotite calculate mai sus, dacă încărcarea exterioară se completează cu încă un moment M (ca în figura alăturată), plasat simetric cu primul, dar având acelaşi sens de rotaţie cu acela (cele două momente fiind deci antisimetrice).

Rezolvare



Fig. 6.19

În această situaţie calculul este mult simplificat prin secţionarea imaginară a barei pe axa ei de simetrie; gradul de nedeterminare se reduce astfel la 1 (în necunoscuta T), eforturile N şi M fiind nule în acea secţiune, deoarece corespund unor diagrame antisimetrice.
Bara poate fi studiată pe o jumătate (fig. 6.19), cu sistemul de bază şi împărţirea în regiuni alese cu totul asemănător ca în rezolvările aplicaţiilor precedente.
Cele două stări fictive ale metodei eforturilor sunt arătate în figura 6.20, pe care sunt prezentate şi diagramele care corespund acelor stări de solicitare: expresiile eforturilor sunt foarte simple şi se poate face abstracţie de ele în această etapă, întrucât graficele se trasează cu uşurinţă şi permit aplicarea, pentru calculul coeficienţilor δij, a algoritmului de înmulţire grafică a diagramelor, aşa cum se arată în continuare.


Fig. 6.20

Din ecuaţia metodei eforturilor rezultă:

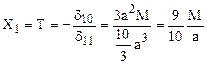
Această valoare se introduce pe schema de solicitare din figura 6.19 şi se stabilesc expresiile eforturilor secţionale pentru jumătatea din stânga a barei reale:



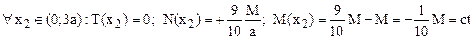
Fig. 6.21

Folosind aceste date se trasează diagramele de eforturi pentru bara reală, mai întâi pe jumătatea ei din partea stângă, după care diagrama T(x) se prelungeşte prin simetrie, iar diagramele N(x) şi M(x) prin antisimetrie, pe întreaga lungime a barei, aşa cum se prezintă în figura următoare.

Este interesant de remarcat, pe aceste diagrame, că eforturile secţionale necunoscute N, T, M (dintre care doar T era nenul) plasate la începutul rezolvării în secţiunea imaginară de pe axa de simetrie a barei coincid cu valorile din acea secţiune din diagramele eforturilor respective.
Pe de altă parte, solicitarea periculoasă are loc tot în secţiunile de la capetele segmentului orizontal al barei, unde calculul se face numai pentru încovoiere, astfel:


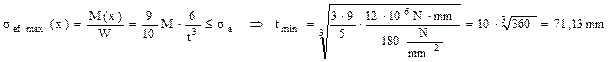
Rezultă că secţiunea pătrată cu latura de 72mm este suficientă pentru bara cotită considerată. Adăugarea celui de-al doilea moment măreşte latura secţiunii cu 20%, iar consumul de material pentru realizarea barei – cu 44%.

6.6. Să se traseze diagramele de eforturi pentru construcţia solicitată ca în figura următoare.

Fig. 6.22

Rezolvare
Obiectul acestei aplicaţii este o bară cotită închisă, simetrică în formă, dar solicitată nesimetric. Din acest motiv nu sunt posibile simplificări majore la rezolvarea triplei nedeterminări statice interioare. Secţionarea imaginară se poate face într-un punct oarecare al conturului, dar avantajos este să se aleagă mijlocul laturii orizontale din partea de jos (fig. 6.22).



Fig. 6.23

Pe schiţa din partea dreaptă a figurii anterioare se prezintă atât modul în care se obţine sistemul de bază, cât şi diagrama de momente din starea fictivă „0” a metodei eforturilor. Diagramele celorlalte trei stări imaginare de încărcare sunt date în figura 6.23. Se poate observa că secţionarea pe axa de simetrie face ca solicitările şi diagramele „1” şi „3” să fie simetrice, iar cele de la starea „2” – antisimetrice, ceea ce uşurează trasarea graficelor.
În plus, cei nouă coeficienţi δij se calculează simplu prin înmulţirea grafică a diagramelor din stările fictive de încărcare, astfel:


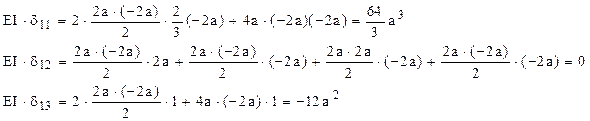
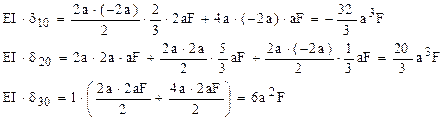
Observaţie importantă
Doi dintre coeficienţii calculaţi aici au rezultat de valori nule; dacă se urmăreşte cauza acestei situaţii, se poate înţelege că termenii din sumele respective se reduc, în perechi, pentru că ei sunt obţinuţi înmulţind o diagramă simetrică („1” sau „3”) cu una antisimetrică („2”); astfel de combinaţii sunt întâlnite şi în alte tipuri de aplicaţii, în care va fi util să se observe direct că rezultatul acestor înmulţiri este zero!

Cu valorile de mai sus ale coeficienţilor se scriu cele trei ecuaţii ale metodei eforturilor (simplificând peste tot prin EI), după cum urmează:

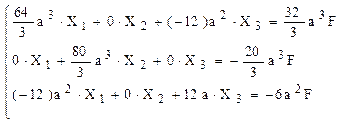
Rezolvarea acestui sistem este practic imediată şi se obţine că:

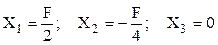
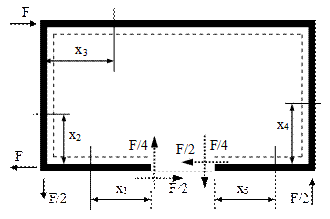
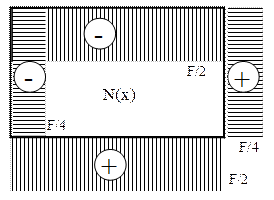
Aceste valori se introduc pe cele două feţe ale tăieturii imaginare făcute în bara cotită închisă din această problemă, pentru care încărcările toate sunt reprezentate în figura 6.24a de mai jos, împreună cu modul în care bara este împărţită în regiuni; pe această bază se obţin expresiile analitice ale eforturilor secţionale din bară, cum se arată mai jos.


 
a.                                                        b.
Fig. 6.24

Trebuie remarcat că toate regiunile au lungimea de 2a, cu excepţia regiunii notate cu (x3), care este de lungime 4a, iar expresiile sunt:

N(x1)=N(x5)=+F/2 ;   N(x2)=-F/4 ;   N(x3)=-F/2 ;   N(x4)=+F/4
T(x1)=T(x5)=-F/4 ;   T(x2)=+F/2 ;   T(x3)=-F/4 ;   T(x4)=+F/2
M(x1)=-(F/4)x              de unde            M(0)=0 ,   M(2a)=-aF/2 ;
M(x2)=(F/2)x - (F/4)2a=(F/2)(x-a)         M(0)=-aF/2 ,   M(2a)=+aF/2
M(x3)=-(F/4)x + aF/2                            M(0)=+aF/2 ,   M(4a)=-aF/2
M(x4)=(F/2)(a-x)                                  M(0)=+aF/2 ,   M(2a)=-aF/2
M(x5)=(F/4)x                                       M(0)=0 ,   M(2a)=+aF/2

Diagrama eforturilor axiale este prezentată în figura 6.24.b., iar celelalte două diagrame – în figura 6.25.


Fig. 6.25

Cu aceasta s-au îndeplinit cerinţele aplicaţiei, iar forma diagramelor arată, pe de o parte, că se respectă relaţia diferenţială între efortul tăietor şi cel de încovoiere; pe de altă parte, este interesant de remarcat că diagramele N şi M sunt antisimetrice, iar T simetrică, adică încărcarea barei cotite închise poate fi considerată antisimetrică.



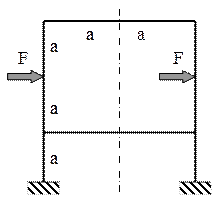
Fig. 6.26

6.7. Să se traseze diagramele de eforturi pentru bara cotită din figura alăturată.

Rezolvare
Construcţia este simetrică, dar şi de trei ori static nedeterminată exterior (datorită celor două reazeme încastrate), având şi o triplă nedeterminare interioară (datorită conturului închis), adică gradul total de nedeterminare este 6. Această cifră se reduce spectaculos prin secţionarea barei pe axa ei de simetrie.


Fig. 6.27

            O astfel de secţionare întâlneşte conturul barei în două puncte, în care trebuie plasate câte trei eforturi necunoscute; încărcarea antisimetrică face ca, dintre acestea, eforturile de tip axial şi încovoietor să fie nule, în ambele tăieturi imaginare. Rezultă că gradul de nedeterminare este redus la 2, iar singurele necunoscute care mai trebuie calculate sunt forţele tăietoare din secţiunile de pe axa de simetrie, aşa cum se arată în figura 6.27.
Metoda eforturilor este calea cea mai rapidă pentru rezolvarea nedeterminării, iar diagramele de eforturi pentru cele trei stări fictive de încărcare sunt în totalitate liniare şi uşor de trasat (fig. 6.28), încât coeficienţii δij se pot calcula prin metoda grafică.



Fig. 6.28


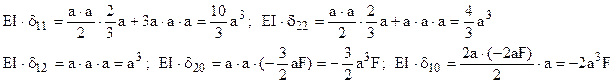
Folosind aceste rezultate, ecuaţiile metodei eforturilor se scriu astfel:


Rezolvând aceste ecuaţii se obţin valorile: X1 = (21/62)F şi X2 = (27/31)F, care reprezintă eforturile tăietoare din secţiunile făcute pe axa de simetrie a construcţiei analizate. După ce se plasează aceste forţe pe schema de solicitare din figura 6.27 de mai sus, în care se observă că toate cele cinci regiuni au lungimea a, expresiile eforturilor secţionale din bară capătă următoarea formă:

N(x1) = N(x4) = 0 ;   N(x2) = N(x3) = N(x5) = (75/62)F
T(x1) = -(21/62)F ;   T(x4) = -(27/31)F ;   T(x2) = 0 ;   T(x3) = T(x5) = F
M(x1) = (21/62)Fx ;               cu   M(0) = 0 ;  M(a) = (21/62)aF
M(x4) = (27/31)Fx ;               cu   M(0) = 0 ;  M(a) = (27/31)aF
M(x2) = ct = (21/62)aF ;  
M(x3) = (21/62)aF - Fx ;        cu   M(0) = (21/62)aF ;  M(a) = -(41/62)aF
M(x5) = -(41/62)aF + (27/31)aF - Fx = (13/62)aF - Fx ;
cu  M(0) = (13/62)aF;  M(a) = -(49/62)aF


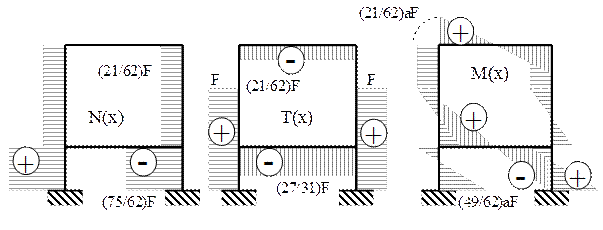
Fig. 6.29

Cu aceste valori se trasează diagramele de eforturi pe jumătatea din stânga a construcţiei, după care acestea se prelungesc prin antisimetrie (N şi M) şi prin simetrie (T) pe întreaga lungime a barei (fig. 6.29).

Se observă că solicitarea periculoasă se produce în secţiunile din reazemele încastrate ale barei, unde atât eforturile de încovoiere, cât şi cele axiale au valorile cele mai mari. Dacă se admite că secţiunile transversale sunt de formă pătrată, cu latura t, atunci condiţia de rezistenţă se scrie:


    

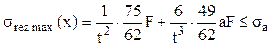
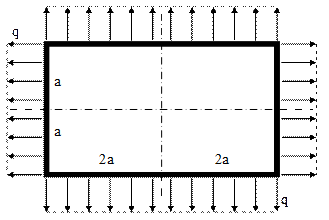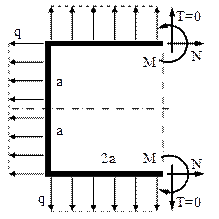
Fig. 6.30

6.8. Să se traseze diagramele de eforturi pentru construcţia solicitată ca în figura următoare.
Rezolvare
Acest cadru închis are două axe de simetrie, inclusiv pentru încărcările lui, alcătuite din forţe distribuite cu intensitatea q; ambele simetrii se vor folosi pentru secţionarea barei, începând de exemplu cu axa verticală, aşa cum se arată în schema din partea dreaptă a figurii de mai sus. Cele două tăieturi imaginare determină introducerea câte unui grup de trei eforturi necunoscute N, T şi M, simetrice în perechi, datorită existenţei celei de-a doua simetrii.
Statica nedeterminare interioară poate fi scăzută la gradul n=1 dacă se analizează două aspecte particulare ale problemei:



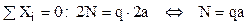
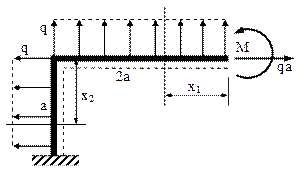
Fig. 6.31

Pe această bază rămâne de studiat un sfert din cadrul iniţial (fig. 6.31), iar acesta se obţine tăind imaginar bara pe axa orizontală de simetrie. Pentru a evita introducerea unui grup nou de necunoscute interioare, în noua secţiune se imaginează un reazem încastrat; trebuie menţionat că acest artificiu nu contrazice modul în care bara se deformează, întrucât din simetria ei constructivă şi de încărcare rezultă că în toate secţiunile aflate pe cele două axe de simetrie deplasările unghiulare (rotirile) sunt egale cu zero!
S-a ajuns la o construcţie simplu static nedeterminată, o bară cotită formată din două segmente îmbinate în unghi drept şi având ca necunoscută valoarea momentului M; cea mai rapidă metodă pentru stabilirea acestei valori este probabil cea bazată principial pe teorema lui Castigliano.
În vederea aplicării acestei metode, se începe cu stabilirea eforturilor de încovoiere din bara considerată:

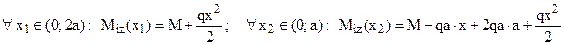
S-a arătat anterior că derivatele parţiale ale lucrului mecanic elastic trebuie să fie nule inclusiv în raport cu necunoscutele static nedeterminate interioare, deci se va scrie că:

Ecuaţia astfel obţinută se dezvoltă după cum urmează:


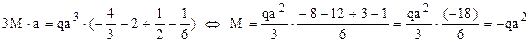
Introducând această valoare pe schema de solicitare din figura 6.31, se ajunge la următoarele expresii şi respectiv diagrame ale eforturilor secţionale de pe sfertul de cadru considerat:


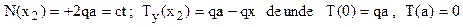
Fig. 6.32


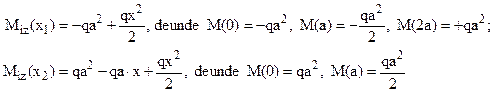
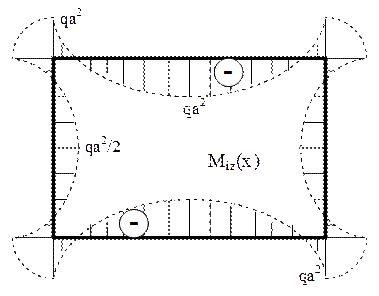
Fig. 6.33

Rezultatele de mai sus au fost folosite la trasarea diagramelor de eforturi din figurile 6.32 şi 6.33, la care se observă că sunt respectate regulile privind simetria şi antisimetria; în plus, valorile celor trei eforturi interioare static nedeterminate introduse la începutul rezolvării, se regăsesc în diagrame, în dreptul secţiunilor de pe axa de simetrie verticală a construcţiei.

În finalul acestui capitol sunt necesare câteva precizări asupra calculului deplasărilor pentru barele cotite simetrice; se pleacă de la observaţia că, la fel ca pentru rezolvarea nedeterminărilor, eforturile de încovoiere au, dintre toate efectele încărcărilor exterioare ale barelor, influenţa principală în producerea deplasărilor secţiunilor transversale.
Prin urmare, la aplicarea teoremei Mohr-Maxwell, solicitarea şi diagrama reală de încovoiere trebuie înmulţite cu cele fictive, date de încărcarea unitară potrivită cazului abordat. Din constatările făcute anterior asupra înmulţirii diagramelor simetrice cu cele antisimetrice şi observând că solicitarea fictivă cu o forţă unitară pe o axă de simetrie a unei construcţii, pe direcţia acestei axe, duce la o diagramă de momente simetrică, în vreme ce cazul similar cu moment unitar duce la o diagramă antisimetrică, se pot face următoarele afirmaţii, în legătură cu construcţiile simetrice:

Pentru a înţelege mai bine aceste lucruri, se poate analiza cazul barei cotite din aplicaţia anterioară, notată cu 6.7. Diagrama ei de momente este antisimetrică, iar pentru calculul deplasărilor liniare verticale ale celor două secţiuni de pe axa verticală de simetrie diagramele stărilor fictive vor fi simetrice; înmulţirea lor cu diagrama reală duce la rezultate nule şi deci deplasările respective au valoarea zero, aşa cum s-a arătat şi mai sus.