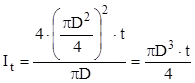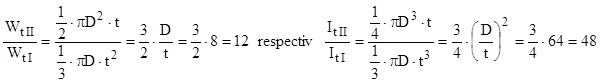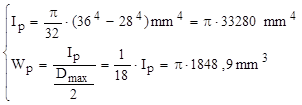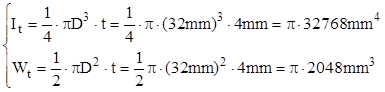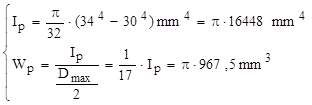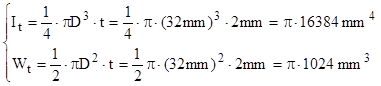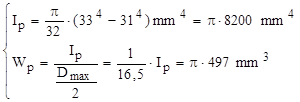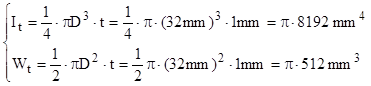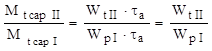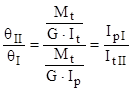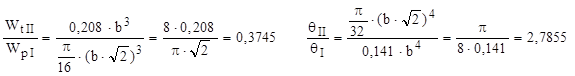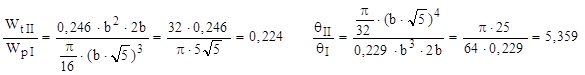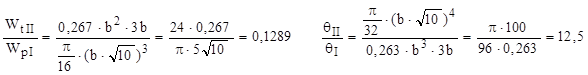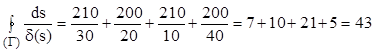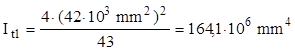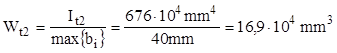Aspecte generale
În cadrul prezentării solicitărilor simple ale barelor drepte, discuţiile asupra răsucirii au fost limitate la secţiunile circulare, pentru care deformaţiile sub acţiunea momentelor de torsiune se produc fără ca aspectul exterior al barelor să se modifice. Mai precis, secţiunile transversale capătă deplasări de rotaţie, dar nici un fel de deformaţii liniare, făcând să se respecte ipoteza (lui Bernoulli) privind secţiunile plane şi perpendiculare pe axa unei bare, care îşi păstrează aceste caracteristici după producerea deformării.
Lucrurile se petrec diferit dacă secţiunile transversale nu sunt circulare, în primul rând pentru că deformaţiile de răsucire provoacă deplanări ale acestor secţiuni, iar aspectul barelor se modifică în mod pregnant şi vizibil. Calculul riguros al acestor bare este laborios, dar există mai multe categorii mari de secţiuni pentru care se pot folosi relaţii comune, pentru calculul de rezistenţă şi de rigiditate, reprezentând generalizări ale celor de la secţiunile circulare.
Prin analogie cu acelea, se porneşte de la definirea unor caracteristici generalizate ale secţiunilor, special destinate calculelor de răsucire, denumite generic moment de inerţie It, respectiv modul de rezistenţă Wt şi având formule de calcul particulare pentru fiecare categorie de secţiuni. Pe baza lor se calculează tensiunile maxime din orice secţiune, care nu trebuie să depăşească rezistenţa materialului barei:
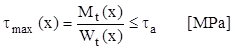 (8.1)
(8.1)
dar şi deformaţiile produse pe un tronson de bară de lungime L, ale cărui capete sunt acţionate de momentele Mt şi se rotesc reciproc cu unghiul Δφ; mărimea calculată este rotirea specifică θ, având şi ea o relaţie similară celei de la secţiunile circulare:
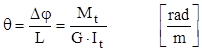 (8.2)
(8.2)
Paragrafele următoare detaliază discuţia pentru cele mai importante şi mai frecvent întâlnite categorii de secţiuni necirculare; obiectivul central este particularizarea relaţiilor de calcul privind caracteristicile secţiunilor, iar partea finală a capitolului se ocupă cu folosirea în aplicaţii a acestor noţiuni.
A. Bare cu secţiuni dreptunghiulare
Analiza riguroasă a comportării acestor bare la răsucire a fost făcută pentru prima dată de Barré de Saint Venant, la mijlocul secolului XIX. Ea este inclusă în cursurile de teoria elasticităţii, iar aici îi vor fi prezentate doar concluziile.
Deformarea la răsucire a barelor din această categorie poate fi observată cu uşurinţă la barele din fier forjat prezente în multe construcţii, mai mult sau mai puţin ornamentale. Principala particularitate este că valorile tensiunilor variază în mod complex în punctele oricărei secţiuni transversale, astfel încât depind de ambele coordonate ale punctelor.
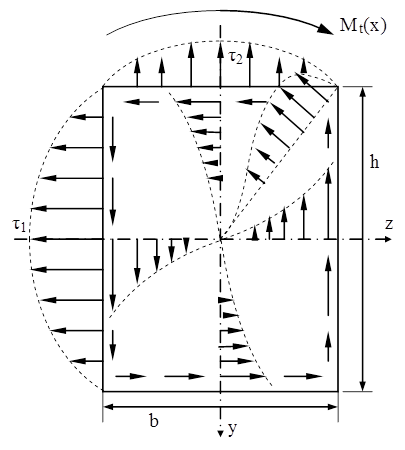
Fig. 8.1 |
Din acest motiv, prezentarea lor grafică se face pe diagrame multiple, ca în figura alăturată. Tensiunile sunt nule în centrul secţiunii, dar şi în colţurile ei (astfel că graficul pe diagonale are un aspect curbiliniu particular), în schimb variază după legi de tip parabolic pe lungimea fiecărei laturi. Pe această bază, tensiunile cele mai mari de pe o secţiune (τ1) se obţin la mijlocul laturii cu cea mai mare lungime.
Pe axele de simetrie ale secţiunii repartiţia tensiunilor se apropie de aceea liniară, proprie secţiunilor circulare, iar raportul dintre tensiunile maxime este constant, pentru secţiunile cu aceeaşi proporţie între laturile dreptunghiului. Această proporţie (h/b) este determinantă şi pentru mărimea caracteristicilor generalizate de răsucire ale acestei categorii de secţiuni, pentru care s-a stabilit că sunt adevărate următoarele relaţii de calcul, în funcţie de laturile secţiunii, respectiv de tensiunea maximă τ1:
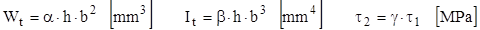 (8.3)
(8.3)
Coeficienţii din aceste relaţii sunt indicaţi în cărţile de specialitate sau în diverse categorii de baze de date inginereşti, aşa cum se exemplifică în tabelul de mai jos.
Valorile coeficienţilor din relaţiile de calcul la răsucire
(pentru secţiuni în formă de dreptunghi)
h/b |
1 |
1,5 |
1,75 |
2 |
2,5 |
3 |
4 |
6 |
8 |
10 |
(>10) |
α |
0,208 |
0,231 |
0,239 |
0,246 |
0,258 |
0,267 |
0,282 |
0,299 |
0,307 |
0,313 |
0,333 |
β |
0,141 |
0,196 |
0,214 |
0,229 |
0,249 |
0,263 |
0,281 |
0,299 |
0,307 |
0,313 |
0,333 |
γ |
1 |
0,859 |
- |
0,795 |
- |
0,753 |
0,745 |
0,743 |
0,743 |
0,743 |
0,743 |
Este remarcabil faptul că, atunci când disproporţia laturilor creşte, valorile coeficienţilor α şi β devin egale şi se apropie tot mai mult de 1/3. Pe această bază relaţiile de mai sus pot fi scrise simplificat, pentru secţiunile denumite dreptunghiuri înguste, astfel:
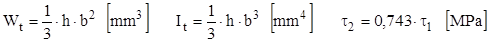 (8.4)
(8.4)
Ca principiu, se înscriu în această categorie secţiunile care au raportul laturilor egal cel puţin cu 10, dar în multe situaţii practice se asimilează acestei grupări şi secţiuni cu valori ceva mai mici ale acestui raport.
B. Bare cu secţiuni simplu conexe
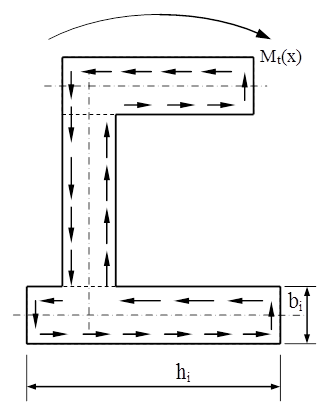
Fig. 8.2
|
Se numesc astfel secţiunile al căror contur poate fi parcurs în mod continuu, fără ca instrumentul de scris să necesite salturi pe hârtie. Formele lor pot fi diverse, dar adeseori permit a fi descompuse în dreptunghiuri înguste (fig. 8.2), ceea ce reprezintă fundamentul pentru calculul lor.
Tensiunile se repartizează practic liniar pe lăţimea dreptunghiurilor elementare, fiind nule pe axele lor de simetrie şi crescând către laturi, pe care se orientează în sensuri opuse. Se ajunge astfel ca pe întregul contur să se formeze un fel de circuit închis al tensiunilor de răsucire, care au însă valori diferite de la un punct la altul.
Diferenţa provine din faptul că tensiunile de pe dreptunghiurile elementare ajung la valori maxime cu atât mai mari cu cât lăţimea dreptunghiului este mai mare, iar pe lungimea laturilor variaţia este parabolică, cu maximele la mijlocul laturilor. Prin urmare, tensiunile cele mai mari de răsucire la aceste secţiuni simplu conexe se înregistrează la mijlocul laturilor lungi ale dreptunghiului elementar de lăţime maximă [max{bi}].
Calculele de rezistenţă şi de rigiditate se fac după relaţiile generale (8.1) şi (8.2), iar caracteristicile generalizate ale secţiunilor se stabilesc astfel:
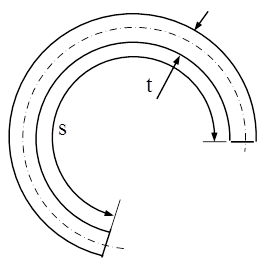
Fig. 8.3 |
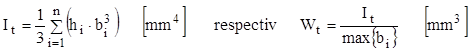 (8.5)
(8.5)
Un caz particular, de secţiune formată dintr-un singur dreptunghi îngust, având însă laturile lungi curbilinii, este prezentat în figura alăturată. Aici sunt importante ca dimensiuni „lăţimea” t a profilului, constantă de obicei pe toată „lungimea”, care se notează cu s şi se măsoară pe curba mediană a secţiunii.
Caracteristicile de răsucire se obţin ca la dreptunghiuri:
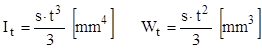 (8.6)
(8.6)
iar valoarea cea mai mare a tensiunilor tangenţiale se produce la mijlocul lungimii s a profilului curbiliniu.
C. Bare cu secţiuni dublu conexe
O secţiune transversală se numeşte dublu conexă atunci când conturul ei este format, la modul general, din două linii curbe închise, de forme arbitrare, care se includ una pe alta fără să se atingă. Barele cu astfel de secţiuni se înscriu între cele tubulare şi se admite despre ele că au aceeaşi secţiune transversală pe întreaga lor lungime.
Se imaginează o asemenea secţiune (fig. 8.4), solicitată la răsucire de momentul Mt. Caracteristicile de rezistenţă şi de rigiditate vor depinde de aria Ω, mărginită de curba mediană (închisă) a profilului notată cu Γ, precum şi de grosimea acestuia (presupusă a fi relativ mică), notată cu δ(s), întrucât variază ca mărime (în principiu) pe curba Γ.
Tensiunile tangenţiale produse prin răsucirea barei sunt, în fiecare punct al secţiunii, paralele cu direcţia tangentei la linia mediană a profilului şi au sensul opus momentului care produce solicitarea; în plus, se admite că în orice punct tensiunile sunt repartizate uniform pe grosimea profilului.
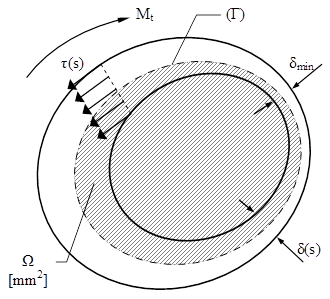
Fig. 8.4 |
Din echilibrul forţelor care acţionează pe un element de volum din peretele barei se obţine condiţia importantă că produsul dintre tensiunile τ(s) şi grosimea δ(s) este constant în orice punct al curbei mediane a profilului. Acest produs e numit flux al tensiunilor tangenţiale şi constanţa lui arată că tensiunile sunt mari unde grosimea este mică şi reciproc. Prin urmare, cea mai mare tensiune se va produce în dreptul grosimii minime δmin a profilului.
Aceste constatări au o anumită corespondenţă în modul cum se calculează caracteristica de rezistenţă a profilelor dublu conexe, pentru care pe baza ecuaţiei de echivalenţă a acestei solicitări se obţine relaţia:
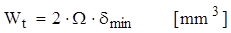 (8.7)
(8.7)
Relaţia de calcul pentru caracteristica de rigiditate se demonstrează pornind de la expresia energiei potenţiale de deformare elastică acumulată prin solicitările de acest fel în barele cu secţiuni dublu conexe; sunt necesare calcule ceva mai laborioase, iar expresia finală se scrie astfel:
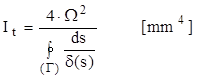 (8.8)
(8.8)
Este interesant de semnalat felul cum se modifică această relaţie pentru secţiunile tubulare care au grosimea peretelui constantă – δ(s) = ct = δ; în aceste cazuri mărimea δ poate fi scoasă în factor şi extrasă în afara integralei de la numitor, făcând ca integrala pe curba închisă Γ să reprezinte lungimea acestei curbe, care poate fi notată prin L(Γ) [mm]. Pe aceste baze relaţia momentului de inerție la răsucire devine:
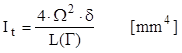 (8.9)
(8.9)
Se mai deduce faptul că la aceste secţiuni tensiunile tangenţiale au aceeaşi valoare în toate punctele din peretele barei.
Aplicaţii
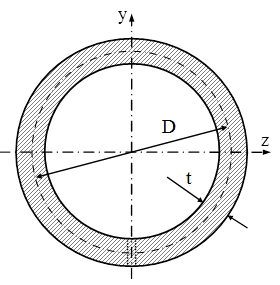
Fig. 8.5
|
8.1. Se consideră o bară cu secţiunea circulară, tubulară (cu pereţi subţiri), constantă ca dimensiuni pe toată lungimea, având particularitatea că diametrul său mediu D este de 8 ori mai mare decât grosimea t a tablei din care este făcută, prin rulare.
Bara are lungimea oarecare L şi este încărcată la răsucire prin momentele exterioare Mt care sunt aplicate la capetele ei. Să se compare rezistenţa şi rigiditatea barei, în două situaţii constructive:
I. fără aplicarea sudurii pe generatoarea ruloului de tablă;
II. cu închiderea conturului, prin cordon de sudură aplicat pe întreaga lungime a generatoarei barei.
Rezolvare
I. Dacă profilul este deschis, atunci calculul se face folosind relaţiile (8.6), în care lungimea arcului de cerc ce reprezintă linia mediană este s = πD, iar caracteristicile secţiunii vor fi:
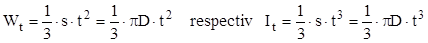
II. După aplicarea sudurii, profilul (cu pereţi subţiri) devine dublu conex, iar pentru modulul de rezistenţă se aplică relaţia (8.7), astfel:
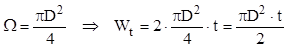
Pentru calculul momentului de inerţie se observă că sunt îndeplinite condiţiile pentru aplicarea relaţiei (8.9), sub forma:
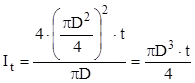
Comparaţia cerută de problemă se realizează raportând rezultatele din a doua serie la cele de la profilul deschis. Astfel, se obţine că:
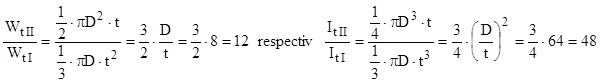
Aşadar, profilul închis este mult mai rezistent şi mai rigid decât cel deschis!
8.2. Să se analizeze diferenţele, la stabilirea caracteristicilor secţionale de răsucire, între rezultatele date de calculul riguros, respectiv de relaţiile de la secţiunile dublu conexe, pentru o bară similară celei de la aplicaţia 8.1, cazul profilului închis cu sudură, pentru diferite valori ale raportului t/D, între grosimea peretelui şi diametrul mediu al secţiunii.
Rezolvare
Pentru a observa deosebirile între cele două modalităţi de calcul, se vor aborda trei variante de secţiuni cilindrice închise, având comună valoarea diametrului mediu D = 32mm, dar valori diferite pentru Dmin şi Dmax.
a. Dmin = 28mm, Dmax = 36mm → D = 32mm, t = 4mm
Se obţine că raportul dimensiunilor este t/D = 4/32 = 1/8 = 0,125
Relaţiile exacte, de la secţiunile circulare inelare, dau:
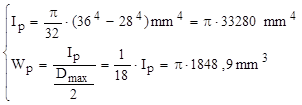
Dacă se folosesc relaţiile de la secţiunile dublu conexe, aşa cum s-a arătat la aplicaţia precedentă, se obţine:
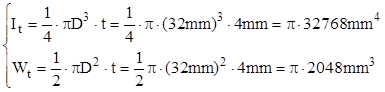
Prin calculul aproximativ s-a ajuns la un rezultat mai mic cu 1,54% pentru momentul de inerţie şi mai mare cu 10,77% (diferenţă mult mai mare decât eroarea permisă în calculele inginereşti) în cazul modulului de rezistenţă, deci calculul exact este acceptabil doar în calculul de rigiditate.
b. Dmin = 30mm, Dmax = 34mm → D = 32mm, t = 2mm
Se obţine că raportul dimensiunilor este t/D = 2/32 = 1/16 = 0,0625
Relaţiile exacte dau:
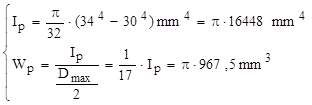
Folosind relaţiile aproximative se obţine:
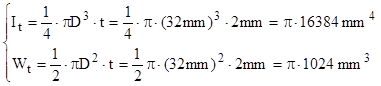
Diferenţele, în acest caz, sunt de -0,39% la evaluarea rigidităţii şi de +5,8% la calculul modulului de rezistenţă la răsucire. Erorile au scăzut foarte mult, dar cea de la calculul Wt este încă destul de mare, plasând rezultatul cu puţin în afara domeniului de abatere permis.
c. Dmin = 31mm, Dmax = 33mm → D = 32mm, t = 1mm
Se obţine că raportul dimensiunilor este t/D = 1/32 = 0,03125
Relaţiile exacte dau:
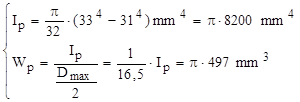
Folosind relaţiile aproximative se obţine:
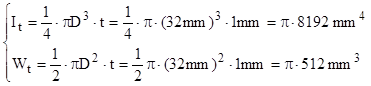
Aceste rezultate sunt convenabil de apropiate de cele exacte, diferenţele fiind de -0,1% pentru momentul de inerţie şi de +3% pentru modulul de rezistenţă.
Prin urmare, secţiunile tubulare cu pereţi subţiri pot fi calculate la fel ca secţiunile dublu conexe, rezultatele fiind cu atât mai precise cu cât grosimea peretelui t este mai mică faţă de diametrul mediu D al secţiunii. În cazul parametrului Ip, acesta poate fi foarte bine aproximat prin It încă de la valori relativ mari ale raportului t/D (aici s-a exemplificat cu valoarea 1/8).
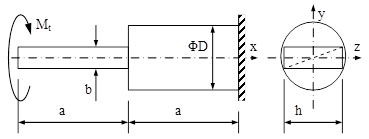
Fig. 8.6
|
8.3. O bară de secţiune circulară plină, solicitată la răsucire prin momentul Mt, aplicat la capătul ei, trebuie prelucrată prin aşchiere astfel ca pe o jumătate din lungime bara să aibă secţiune dreptunghiulară, de laturi h şi b; să se analizeze scăderile de rezistenţă/rigiditate produse prin micşorarea de secţiune, pentru trei variante de dimensiuni ale secţiunii:
a. h = b; b. h = 2b; c. h = 3b.
Rezolvare
Câteva aspecte ale problemei sunt valabile pentru toate variantele de secţiuni dreptunghiulare ce vor fi abordate. Astfel, capacitatea fiecărei porţiuni de bară de a rezista la răsucire se evaluează prin momentul maxim Mt cap pe care aceasta îl poate suporta, iar această mărime este proporţională cu modulul de rezistenţă de pe regiunea respectivă.
Dacă se notează cu I situaţia iniţială, a barei cu secţiune circulară, respectiv cu II – situaţia regiunii cu secţiunea micşorată prin aşchiere, atunci raportul momentelor capabile se va calcula astfel:
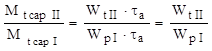
Pe de altă parte rigiditatea celor două regiuni, exprimată prin unghiul specific de răsucire θ, este invers proporţională cu momentul de inerţie, deci raportul rigidităţilor se va scrie:
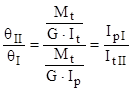
Pentru porţiunea de secţiune circulară plină caracteristicile sunt:
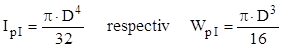
Mai este de remarcat (fig. 8.6) faptul că dimensiunile secţiunii reduse nu sunt independente de diametrul cercului iniţial; acesta reprezintă diagonala în dreptunghiul obţinut prin aşchiere, adică este adevărată relaţia:
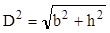
Rămâne să se aplice aceste relaţii în analiza fiecărui caz dimensional.
a. Dacă b = h înseamnă că secţiunea redusă are formă de pătrat, pentru care coeficienţii din relaţiile (8.3) sunt α = 0,208 şi β = 0,141, iar diametrul cercului iniţial este 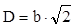 . Caracteristicile de răsucire vor fi:
. Caracteristicile de răsucire vor fi:
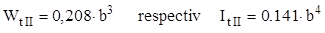
Relaţiile de comparaţie între cele două regiuni ale barei se scriu astfel:
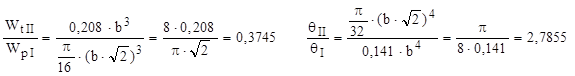
Aceste rezultate arată că, dacă secţiunea se micşorează la un pătrat, atunci rezistenţa la răsucire scade, pe acea porţiune de bară, cu peste 62%, iar deformabilitatea creşte de aproape 2,8 ori (sau rigiditatea scade tot de atâtea ori), adică slăbirea barei este destul de consistentă.
b. Dacă h = 2b, atunci 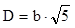 , iar coeficienţii sunt α = 0,246 şi β = 0,229, încât relaţiile de comparaţie devin:
, iar coeficienţii sunt α = 0,246 şi β = 0,229, încât relaţiile de comparaţie devin:
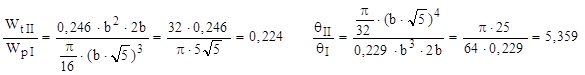
Pentru acest caz, rezistenţa scade cu mai mult de 77%, iar rigiditatea de aproape 5,4 ori.
c. Dacă h = 3b, atunci 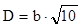 , coeficienţii sunt α = 0,267 şi β = 0,263, iar relaţiile de comparaţie devin:
, coeficienţii sunt α = 0,267 şi β = 0,263, iar relaţiile de comparaţie devin:
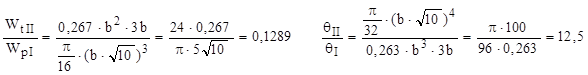
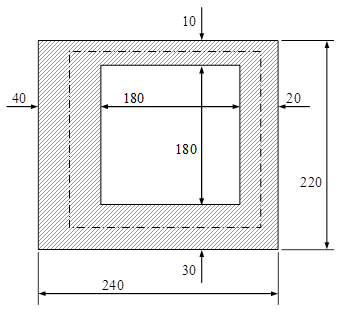
Fig. 8.7 |
Această slăbire a secţiunii micşorează rezistenţa la răsucire a barei cu 87%, iar rigiditatea de 12,5 ori. Prin urmare, trecerea de la secţiunea circulară plină la dreptunghi scade accentuat calităţile barei de a suporta momente de răsucire (ceea ce rămâne adevărat inclusiv dacă secţiunea este redusă pe o porţiune foarte mică din bară!), efectele fiind cu atât mai defavorabile cu cât se accentuează disproporţia dintre laturile dreptunghiului.
8.4. Se consideră o bară având secţiunea transversală cu forma din figura alăturată (desenul nu respectă exact proporţiile dintre dimensiunile secţiunii).
Să se evalueze rezistenţa şi rigiditatea ei la răsucire şi să se analizeze cum se modifică aceste caracteristici atunci când secţiunea se deschide printr-o tăietură transversală, într-un punct oarecare al profilului, pe toată grosimea peretelui şi pe toată lungimea barei.
Rezolvare
În starea iniţială bara are secţiunea de tip dublu conex, iar curba mediană închisă este un patrulater de arie Ω = 210mm×200mm = 42000mm2.
Grosimea minimă a profilului este δmin = 10mm, astfel încât modulul de rezistenţă la răsucire al secţiunii va fi: Wt1 = 2 Ω·δmin = 84×104mm3.
Integrala, calculată pe lungimea curbei mediane închise, care apare la numitorul relaţiei (8.8), cu care se determină momentul de inerţie la răsucire, se reduce la o sumă de fracţii constante, dacă se observă că există segmente ale curbei mediane pe care grosimea profilului este constantă:
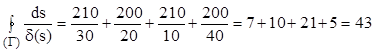
Observaţii
- Fiind o sumă de rapoarte între lungimi, acest rezultat nu are dimensiuni (este un număr abstract).
- Se poate verifica uşor că descompunerea în dreptunghiuri a profilului secţiunii, sugerată de fracţiile din ultima relaţie şi bazată pe segmentarea liniei mediane este corectă şi că s-ar obţine acelaşi rezultat dacă descompunerea s-ar face, de exemplu, împărţind fizic în 4 dreptunghiuri profilul secţiunii.
- Valoarea fracţiilor de mai sus arată că nu toate dreptunghiurile utilizate respectă riguros condiţia precizată, pentru încadrarea între cele înguste, dar o astfel de aproximare este de obicei admisă în practică, mai ales în calcule de genul celor prezente, de evaluare a deosebirilor dintre profilele simplu şi dublu conexe.
Introducând rezultatele de mai sus în relaţia (8.8) se obţine că momentul de inerţie la răsucire pentru bara cu profil dublu conex este:
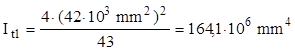
Dacă profilul se decupează, pe toată lungimea, indiferent de punctul lui în care se face decuparea, atunci el devine simplu conex, iar calculul porneşte de la descompunerea secţiunii în dreptunghiuri înguste şi introducerea parametrilor acestora în relaţiile (8.5). De exemplu, folosind decuparea de mai sus a secţiunii, momentul de inerţie la răsucire al secţiunii va fi:

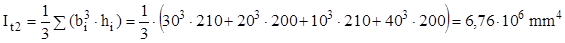
Raportul celor două ultime rezultate arată că prin decuparea longitudinală se produce scăderea parametrului de rigiditate de 24,28 ori, adică bara devine tot de atâtea ori mai uşor de deformat prin răsucire.
Pe de altă parte, caracteristica de rezistenţă se calculează astfel:
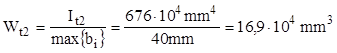
Rezistenţa barei scade, în urma deschiderii profilului, de 4,97 ori! Trebuie remarcat că această scădere se întâmplă indiferent cât de lungă este decuparea pe lungime a barei: dacă într-o singură secţiune transversală are loc deschiderea profilului (de exemplu din cauza unei fisuri longitudinale care străpunge peretele secţiunii), aceasta devine secţiunea periculoasă a barei şi va putea prelua doar momente de 5 ori mai mici decât restul barei!
În concluzie, ultimele două aplicaţii au arătat că secţiunile circulare sunt mult mai rezistente şi mai rigide la răsucire decât cele dreptunghiulare, la fel ca profilele închise (dublu conexe) faţă de cele deschise (simplu conexe).
Observaţii privind ruperea materialelor prin răsucire
Prin încercări de laborator se poate demonstra foarte simplu că materialele cuprinse în categoriile cele mai folosite în ingineria mecanică cedează în moduri diferite, atunci când sunt solicitate la răsucire.
Astfel, pentru o epruvetă (cilindrică, având capetele îngroşate, de secţiune pătrată) dintr-un material tenace ruperea se produce pe o suprafaţă plană şi perpendiculară pe axa longitudinală, adică într-o secţiune transversală propriu-zisă. Explicaţia este că tensiunile tangenţiale maxime se produc pe circumferinţa oricărei secţiuni, loc în care se va produce fisurarea probei, în planul secţiunii transversale de rupere. Secţiunea „netă” rămasă se fisurează din nou pe conturul exterior, unde acţionează tensiunile τmax, aşa încât fisura progresează foarte rapid, cuprinzând întreaga secţiune.
Pe de altă parte, pentru o probă dintr-un material fragil, la care se ştie că rezistenţa la întindere este mult mai mică decât la comprimare, starea de forfecare pură din planele tensiunilor tangenţiale principale de răsucire implică apariţia, în plane înclinate la 45° faţă de acelea, a unor tensiuni de întindere (respectiv de comprimare) de mărimea celor tangenţiale. Acestea sunt tensiunile periculoase pentru material şi din cauza lor se produce ruperea probei după o suprafaţă elicoidală, înclinată mereu la 45° faţă de planele transversale.
Într-o altă ordine de idei, în multe situaţii practice sunt semnificative şi nu pot fi neglijate în calcule tensiunile tangenţiale care se orientează în lungul barelor solicitate la răsucire: conform principiului dualităţii acestor tensiuni, orice τmax dintr-o secţiune transversală are un corespondent longitudinal, egal ca mărime şi orientat la fel faţă de muchia respectivelor două plane.
Aceste tensiuni fac, de exemplu, ca un buştean de lemn relativ uscat să capete fisuri longitudinale, atunci când este solicitat la răsucire. În mod analog, astfel de tensiuni creează pericol şi trebuie introduse în calcule la îmbinările prin nituri sau sudură ale foilor rulate de tablă din care se fac bare tubulare, cu profil închis, încărcate cu momente de răsucire
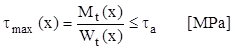 (8.1)
(8.1) 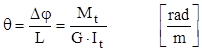 (8.2)
(8.2) 


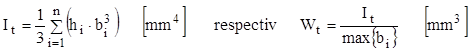 (8.5)
(8.5) 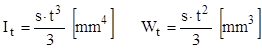 (8.6)
(8.6) 
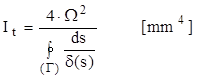 (8.8)
(8.8) 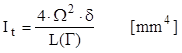 (8.9)
(8.9)