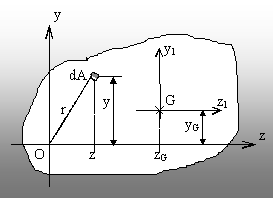
Fig. 2.1

Definiţii

Considerând o suprafaţă plană, de formă oarecare (fig. 2.1), având centrul de greutate în punctul G, se alege un sistem arbitrar de axe perpendiculare între ele (yOz) (în studiul rezistenţei materialelor, axa x coincide, de obicei, cu axa longitudinală a corpului solid). Coordonatele lui G sunt z_G şi y_G. Fie un element de arie (dA), la distanţele y şi z faţă de axele de coordonate, respectiv r – faţă de polul O. În aceste condiţii, se pot defini mai multe caracteristici ale suprafeţei.

1. Aria

(2.1)

Aria este totdeauna o mărime strict pozitivă (fiind zero numai dacă suprafaţa se reduce la un punct).

2. Momentele statice (faţă de axe)

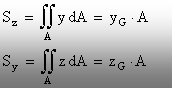[m³] (2.2)

Momentele statice sunt nule în raport cu axele care trec prin centrul de greutate G.

Pentru o suprafaţă de formă complexă care poate fi descompusă în (n) suprafeţe elementare, pentru care se pot calcula ariile A_i şi poziţiile centrelor de greutate G_i, momentele statice globale vor fi:

(2.3)

Aceste relaţii sunt folosite la calculul coordonatelor centrului de greutate pentru suprafeţele complexe, pe baza egalării momentelor statice globale calculate cu (2.3), respectiv cu ultima formă din (2.2).

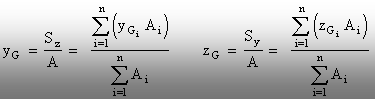(2.4)

3. Momentele de inerţie

a) axiale

[m⁴] (2.5)

Dacă sistemul de axe este dus în centrul de greutate (axe centrale), atunci momentele axiale se numesc centrale.

b) polar

[m⁴] (2.6)

Momentele axiale şi polare sunt mărimi strict pozitive, având valoarea zero numai pentru suprafeţele reduse la un punct.

c) centrifugal

[m⁴] (2.7)

Dacă una dintre axe este axă de simetrie a suprafeţei, atunci momentul centrifugal este nul.

Deoarece raza polară r este legată de coordonatele y şi z prin relaţia (r² = y²+z²), ca laturi ale unui triunghi dreptunghic (fig. 2.1), rezultă că între momentele de inerţie axiale şi cel polar există relaţia:

I_p = I_z + I_y (2.8)

De aici rezultă că, pentru un anumit pol, suma momentelor axiale este un invariant, de valoarea momentului polar, nedepinzând de alegerea axelor de coordonate.

Pentru o suprafaţă de formă complexă care poate fi descompusă în (n) suprafeţe elementare, momentele de inerţie globale se vor calcula (aşa cum se calculează şi aria totală) ca sume algebrice ale momentelor suprafeţelor componente (luând cu semn negativ termenii care corespund unor decupări), cu condiţia ca toate momentele dintr-o asemenea relaţie să fie calculate faţă de un acelaşi sistem de axe.