Momentele de inerţie principale centrale

Dacă se imaginează o bară prismatică, de secţiune dreptunghiulară (de forma unei rigle de plastic), este uşor de înţeles că ea poate fi îndoită mult mai uşor în jurul laturii mai lungi a secţiunii transversale, decât pe direcţia laturii mai scurte. Rezultă că, pentru astfel de bare, rezistenţa la solicitarea descrisă (încovoiere) depinde în mod direct de orientarea secţiunii transversale faţă de direcţia pe care se produce solicitarea.

Se va arăta ulterior că mărimea hotărâtoare în această privinţă este momentul de inerţie al secţiunii faţă de axa de îndoire. În acest sens, o secţiune transversală oarecare va conduce la rezistenţa maximă a barei la încovoiere dacă momentul său de inerţie faţă de axa momentului încovoietor are cea mai mare valoare posibilă.

Trebuie făcută precizarea că barele se consideră a fi rezemate şi solicitate pe axa lor geometrică. Aceasta reprezintă şirul centrelor de greutate ale secţiunilor transversale, astfel că, dintre toate punctele unei secţiuni, în rezistenţa materialelor este important centrul său de greutate.

Caracteristicile de inerţie ale secţiunii vor fi aşadar calculate cu raportare la axe care trec prin G (axe centrale), iar discuţia care urmează, deşi valabilă pentru oricare punct al unei suprafeţe finite plane, se va face cu referire la punctul G.

Se pune problema să se determine valorile extreme (principale) ale momentelor de inerţie axiale, adică este necesar să se deriveze, în raport cu (2a), primele două relaţii (2.10). Se ajunge la anularea acestor derivate pentru situaţiile în care se îndeplineşte condiţia

(2.11)

Deoarece funcţia (tg2a) are perioada (kp), rezultă că soluţia ecuaţiei trigonometrice de mai sus se scrie sub forma:

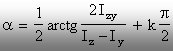(2.12)

Aceste valori de unghi reprezintă înclinările, faţă de sistemul iniţial (yGz), ale axelor de coordonate în raport cu care se obţin valorile extreme ale momentelor de inerţie axiale pentru secţiunea considerată.

Se observă că este vorba, de fapt, despre numai două axe, perpendiculare între ele, una corespunzând valorii maxime (I₁), cealaltă valorii minime (I₂) a momentelor de inerţie. Aceste valori reprezintă momentele de inerţie principale centrale ale secţiunii şi se calculează cu următoarea relaţie:

(2.13)

Axele, duse prin G, care corespund acestor valori se numesc axele principale centrale ale secţiunii. De regulă, acestea vor fi chiar axele y şi z ale reperelor folosite în rezolvarea problemelor întâlnite în studiul rezistenţei materialelor.

Prin urmare, determinarea axelor principale centrale ale secţiunilor transversale ale corpurilor va reprezenta o etapă importantă a rezolvării diverselor situaţii de solicitare.

Atenţie: Din relaţia (2.11) rezultă că vor fi axe principale acele axe pentru care I_zy = 0. După cum s-a precizat anterior, această condiţie este îndeplinită de axele de simetrie ale secţiunii. Prin urmare, oricare axă de simetrie a unei secţiuni plane este axă principală centrală a ei!

Consecinţe:

1. Dacă o suprafaţă plană are o axă de simetrie, aceasta este axă principală centrală, cea de-a doua fiind perpendiculară pe prima, în centrul de greutate.

2. Secţiunile cu mai mult decât două axe de simetrie (cum sunt poligoanele regulate şi, la limită, cercul), au o infinitate de axe principale centrale. În plus, cum valorile maxime şi minime ale momentelor principale sunt egale, rezultă că I₁ = I₂ = I_z = I_y = ct, adică momentele de inerţie axiale centrale ale acestor secţiuni nu depind, ca valoare, de axele alese.

În directă legătură cu momentele principale centrale se definesc alte două caracteristici ale suprafeţelor plane, după cum urmează.

Razele de inerţie (de giraţie)

[m] (2.14)

Modulele de rezistenţă

Se calculează ca raport între momentul de inerţie axial sau polar şi distanţa maximă a unui punct de pe secţiune până la axa (sau punctul) de reper. Sunt de două categorii:

a) axiale

[m³] (2.15)

b) polar

[m³] (2.16)

Atenţie: Pentru suprafeţele compuse, razele de inerţie şi modulele de rezistenţă nu pot fi calculate ca sume algebrice ale valorilor corespunzătoare suprafeţelor elementare, ci numai prin aplicarea definiţiei!