Exemple de calcul

A. Caracteristicile de inerţie ale figurilor geometrice elementare

Fig. 2.3.

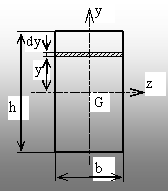
2.1. Dreptunghiul de laturi b şi h

Această secţiune are două axe de simetrie, care vor fi deci axele principale centrale y şi z. Se defineşte, la distanţa y de axa z, un element de arie dA, de formă dreptunghiulară şi laturi b şi dy (fig. 2.3).

Rezultă că aria lui va fi:

dA = b dy

Pentru a verifica dacă abordarea problemei este corectă, se calculează aria dreptunghiului, după definiţia din relaţia (2.1), astfel:

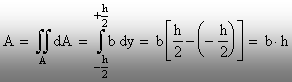(2.17)

Momentul de inerţie faţă de axa (z) fi:

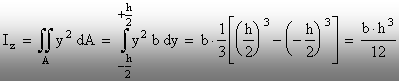(2.18)

Procedând analog, se obţine:

Razele de inerţie:

(2.19)

Modulele de rezistenţă:

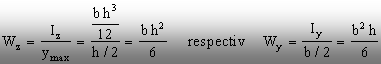(2.20)

Observaţie: Caracteristicile polare sunt importante şi vor fi calculate numai pentru secţiunile circulare!

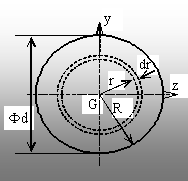
2.2. Cercul de rază R şi diametru d

Fig. 2.3.

Cercul are o infinitate de axe de simetrie, deci oricare diametru al său coincide cu direcţia unei axe principale centrale.

Elementul de arie se alege (fig. 2.3) sub forma unui inel de rază r şi grosime (dr), iar aria lui este: dA = 2p r dr

Aria cercului va fi:

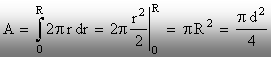
Momentele de inerţie:

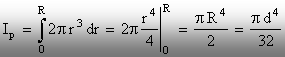(2.21)

Folosind relaţia (2.8) şi egalitatea I_z = I_y, se pot afla momentele axiale:

(2.22)

Razele de inerţie: 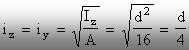(2.23)

Modulele de rezistenţă: (2.24)

(2.25)

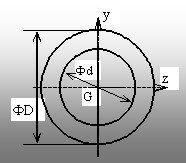
Fig. 2.4.

2.3. Secţiunea circulară inelară cu d_int = d şi d_ext = D (fig. 2.4).

Pe baza rezultatelor de mai sus, momentele de inerţie se calculează prin “scăderea” cercului interior din cel exterior:

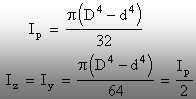(2.26)

Razele de inerţie vor fi:

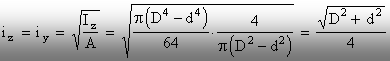(2.27)

Modulele de rezistenţă se calculează după relaţiile de definiţie (2.15)-(2.16):

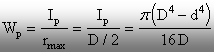(2.28)

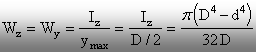(2.29)

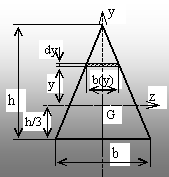
Fig. 2.5.

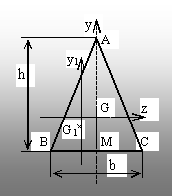
2.4. Triunghiul isoscel, cu baza b şi înălţimea h

Axele principale centrale sunt cele din figura 2.5. Elementul de arie este dreptunghiular, de laturi b(y) şi dy. Pe baza asemănării unor triunghiuri se poate scrie că:

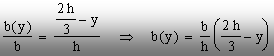
Aria triunghiului şi momentul de inerţie faţă de axa principală centrală (z) vor fi:

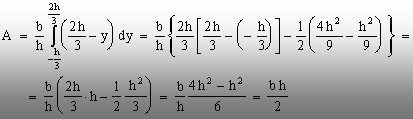
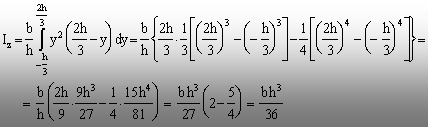(2.30)

Fig. 2.6.

Este uşor de observat că, în acest caz, nu se poate scrie momentul faţă de axa (y) prin permutarea literelor b şi h, deoarece axele au poziţii diferite faţă de laturile triunghiului (axa z este paralelă cu una dintre laturi).

Pentru a folosi, totuşi, rezultatul precedent, se fac notaţiile din figura 2.6, unde M este mijlocul lui BC, iar axa (y₁) trece prin centrul de greutate G₁ al triunghiului ABM.

În aceste condiţii, momentul I_y1(ABM) se poate afla cu o relaţie de forma (2.30) după care, cu relaţia lui Steiner (2.9), se calculează I_y(ABM), aşa cum se arată în expresia (2.31):

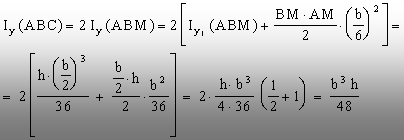(2.31)

Modulele de rezistenţă:

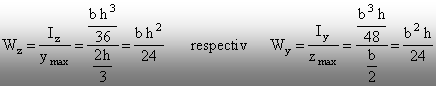(2.32)

Razele de inerţie:

(2.33)

B. Aplicaţii pentru alte secţiuni plane

Rezultatele obţinute în subcapitolul precedent sunt utilizate în mod curent la calculul caracteristicilor unor secţiuni derivate din cele elementare, sau care se descompun în suprafeţe elementare, aşa cum se arată în continuare.

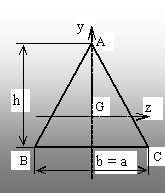
2.5. Triunghiul echilateral de latură a (fig. 2.7)

Fig. 2.7.

Se observă că înălţimea triunghiului poate fi exprimată în funcţie de latura a, astfel:

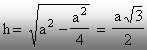
Aplicând relaţiile (2.29) şi (2.30), se pot calcula momentele de inerţie principale centrale:

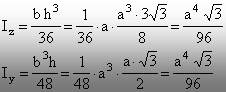
Rezultă că, în cazul triunghiurilor echilaterale, momentele de inerţie centrale sunt invariante, la rotirea axelor (pentru că maximul şi minimul lor au, de fapt, aceeaşi valoare!). Acest fapt se explică, aşa cum s-a arătat mai sus, prin existenţa celor 3 axe de simetrie ale acestor suprafeţe, toate fiind axe principale centrale.

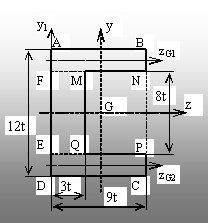
2.6. Secţiune compusă din mai multe figuri geometrice elementare

Fig. 2.8.

Se consideră secţiunea delimitată de punctele ABNMQPCD (fig. 2.8), formată prin decuparea dreptunghiului MNPQ din dreptunghiul ABCD. Să se calculeze momentele de inerţie principale centrale şi modulele de rezistenţă ale acestei secţiuni.

Rezolvare

Se observă că secţiunea admite o axă de simetrie orizontală, care va fi axa principală centrală (z) a secţiunii. Axa (y) va fi perpendiculara pe (z) în centrul de greutate G al întregii secţiuni.

Pentru a determina poziţia pe axa (z) a lui G, se alege o axă (y₁), de exemplu pe latura AD a secţiunii.

Folosind cea de-a doua relaţie (2.4) se calculează coordonata căutată, ţinând seama că centrele de greutate ale dreptunghiurilor elementare se află la distanţele (9/2)t, respectiv [3t + (6/2)t] faţă de axa (y₁).

Rezultă că:

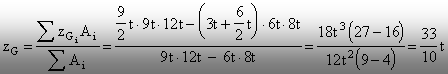
Prin urmare, axa principală centrală (y) va avea poziţia arătată în figura 2.8.

Dacă se începe prin a calcula momentul I_y, alegând descompunerea secţiunii în cele două dreptunghiuri precizate mai sus, ABCD şi MNPQ, se observă că nici unul dintre ele nu are centrul de greutate pe axa globală (y) a secţiunii. Pentru calculul momentului lor faţă de axa (y) se va aplica relaţia lui Steiner, astfel:

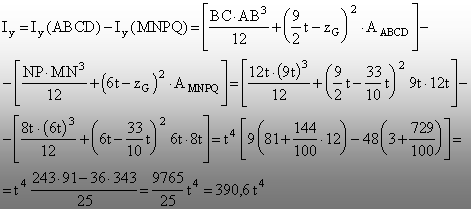
Pentru calculul celuilalt moment principal central, se poate proceda în două moduri.

a) Cu descompunerea secţiunii în cele două dreptunghiuri de mai sus

În acest caz, ambele dreptunghiuri elementare au centrul de greutate pe axa principală globală (z), deci folosirea relaţiei Steiner nu mai este necesară:

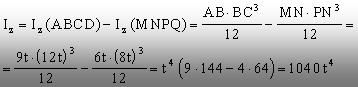
b) Cu descompunerea secţiunii într-un dreptunghi “vertical” FMQE, cu centrul de greutate pe axa (z) şi două dreptunghiuri “orizontale”, ABNF şi EPCD (pe liniile punctate din figura 2.8), având centrele de greutate pe axele (z₁) şi (z₂), care sunt axele lor principale centrale, paralele cu (z).

Momentul global faţă de axa(z) va fi:

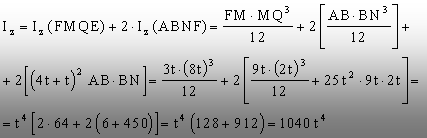
Atenţie: S-a obţinut acelaşi rezultat prin ambele metode, dar calculul a fost mai laborios în cazul al doilea! Rezultă că este important ca descompunerea secţiunilor complexe să se facă în modul care conduce la cele mai simple calcule (ceea ce se învaţă, prin exerciţiu), micşorându-se astfel şi probabilitatea apariţiei greşelilor de calcul.

Pentru determinarea modulelor de rezistenţă ale secţiunii globale, se aplică definiţia acestor mărimi, observând că

y_max = (12/2)t = 6t

z_max = 9t - z_G = 9t - (33/10)t = (57/10)t

Rezultă:

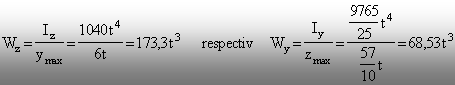
Prin urmare, o grindă cu secţiunea transversală de forma şi proporţiile din figura 2.8 va avea capacitatea maximă de rezistenţă la încovoiere dacă se va orienta cu axa principală centrală (z) pe direcţia momentului încovoietor (adică îndoirea barei se va produce în jurul acestei axe).