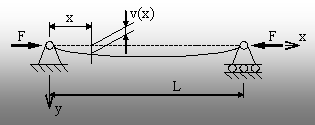
Cazul barei cu rezemare articulată la ambele capete

Fig. 9.1

Dacă se analizează starea deformată a barei din figura 9.1 se remarcă apariţia, în orice secţiune transversală a ei, a unui moment de încovoiere de forma M_iz(x) = F×v(x).

    Prin urmare, ecuaţia (8.12) se poate scrie, pentru această stare de încărcare, astfel:

                                           (9.2)

Dacă se trec toţi termenii în membrul stâng al ecuaţiei şi se face notaţia

                                                   (9.3)

atunci ecuaţia (9.2) devine                             

Soluţia acestei ecuaţii diferenţiale trebuie să fie de forma

v(x) = A sin ax + B cos ax ,

   iar coeficienţii se pot determina impunând condiţiile de deformabilitate a barei (condiţiile la limită), în acest caz – imposibilitatea deplasării ei pe verticală în secţiunile de la capete:

De remarcat că ultima condiţie rezultă din necesitatea de a se evita soluţia banală a ecuaţiei diferenţiale, v(x)=0, iar constanta k poate fi orice număr natural (diferit de zero). Dacă se ia în considerare prima dintre soluţiile posibile (k=1), rezultă că bara deformată are aspect de sinusoidă, având ecuaţia:

Trebuie făcută observaţia că, în această expresie, valoarea maximă (v _max) a deplasării rămâne nedeterminată, ceea ce explică posibilitatea de evoluţie catastrofală a fenomenului de flambaj.

Din condiţia (a×L=p) rezultă valoarea constantei a, care se poate înlocui în relaţia (9.3), astfel:

                      (9.4)

Introducerea lui I _min (cel mai mic dintre momentele de inerţie principale centrale ale secţiunii transversale) în această formulă este justificată de necesitatea de a se stabili cea mai mică dintre posibilele forţe critice de flambaj ale barei studiate.

De altfel, este uşor de intuit faptul că încovoierea barei (sub forţă axială) se produce în mod preferenţial în jurul axei principale centrale (a secţiunii transversale) faţă de care momentul de inerţie este minim.

Relaţia (9.4), numită formula lui Euler pentru cazul fundamental de flambaj, permite calculul forţei critice care corespunde barei solicitate ca în figura 9.1 de mai sus.

Atenţie! Forţa critică trebuie înţeleasă ca nivel al solicitării de compresiune până la care nu se produce pierderea stabilităţii elastice a barei. Rezultă că trebuie luate măsuri pentru ca prin încărcarea piesei să nu se atingă această limită.

Pe de altă parte, trebuie semnalat că se pot scrie şi alte soluţii ale ecuaţiei diferenţiale (9.2), dând lui k alte valori decât 1. Astfel, dacă se adoptă k=2, atunci se obţine că (a×L=2p) care conduce, pentru forţa critică a barei, la următoarea formulă de calcul:

                                         (9.5)

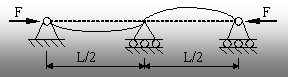
Fig. 9.2

Această valoare a forţei critice corespunde situaţiei în care bara este rezemată suplimentar, la mijlocul lungimii sale, printr-o arti-culaţie mobilă (fig. 9.2).

După cum se observă, această variantă de rezemare este o soluţie practică relativ simplă pentru a mări (de 4 ori) forţa critică de flambaj a barei, deci şi intervalul de funcţionare sigură a ei.

Pentru următoarele soluţii ale ecuaţiei diferenţiale (obţinute din condiţia a×L=kp) se deduce, pe baza unui raţionament asemănător celui de mai sus, că se introduc un număr de (k–1) reazeme mobile intermediare, ceea ce conduce la mărirea de (k²) ori a forţei critice a barei.