Calculul forţei critice pentru alte cazuri de rezemare

Fig. 9.3

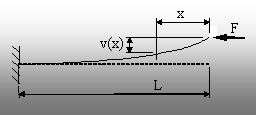
Pentru bara în consolă (fig. 9.3) se remarcă faptul că axa longi-tudinală se curbează, rămânând tangentă la poziţia din momentul anterior producerii solicitării.

    Efortul secţional de încovoiere se calculează cu o relaţie identică celei de la bara articulată la ambele capete, adică

M_iz(x) = F×v(x).

Prin urmare, ecuaţia diferenţială a fibrei deformate se scrie tot sub forma (9.2) şi întregul raţionament făcut anterior se repetă aici, iar singura deose-bire apare în scrierea condiţiilor la limită (după cum s-a ales originea coor-donatei x, rezultă că sunt egale cu zero săgeata barei – în x=0 şi respectiv rotirea ei – în x=L):

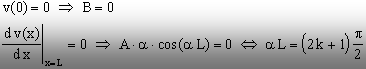
Pentru cea de-a doua condiţie se observă că nici constanta A (care ar însemna că bara nu se curbează deloc) şi nici parametrul a nu pot fi nule, iar din egalitatea cu zero a funcţiei trigonometrice rezultă că argumentul ei trebuie să fie multiplu impar de (p/2). Dacă se ia în considerare prima valoare posibilă, adică aL = p/2,  se ajunge la:

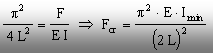                               (9.6)

   adică formula forţei critice de flambaj pentru bara în consolă.

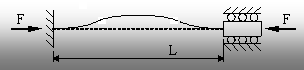
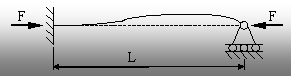
Procedând analog (dar cu rezolvarea unor ecuaţii diferenţiale neomogene) se pot rezolva alte două cazuri de rezemare pentru barele solicitate la compresiune – bara încastrată la ambele capete (fig. 9.4), respectiv încastrată la un capăt şi articulată la celălalt (fig. 9.5).

Forţa critică se calculează, pentru fiecare caz, cu relaţia scrisă în dreptul figurii respective.

Fig. 9.4

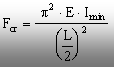  (9.7)

Fig. 9.5

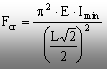  (9.8)

Dacă se analizează relaţiile pentru calculul forţei critice de flambaj pentru cele patru cazuri de rezemare studiate, se poate spune că numitorul fiecărei relaţii reprezintă o mărime caracteristică cazului respectiv de încărcare. Se obişnuieşte să se noteze această mărime prin (L_f²), iar prin L_f să se desemneze “lungimea de flambaj” a barei pentru acea variantă de rezemare.

Din relaţiile de mai sus se pot extrage lungimile de flambaj pentru situaţiile respective, astfel:

Þ pentru bara dublu articulată                     L_f = L

Þ pentru bara în consolă                              L_f = 2L

Þ pentru bara dublu încastrată                     L_f = L/2

Þ pentru bara articulată şi încastrată            L_f = 0,707×L

În acest mod se creează posibilitatea scrierii unei forme unificate a relaţiei lui Euler, pentru calculul forţei critice de flambaj corespunzătoare celor patru tipuri de încărcare studiate:

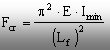                                 (9.9)