Domeniul de aplicabilitate a formulei lui Euler

După cum s-a precizat, în toate cazurile de solicitare de mai sus este vorba despre flambajul elastic, presupunându-se că pierderea stabilităţii barei se produce în domeniul elastic de deformabilitate a materialului ei, adică tensi-unea maximă din piesă nu depăşeşte limita de proporţionalitate (s_p) de pe curba caracteristică (de compresiune).

Dacă se defineşte, pe baza forţei critice dată de formula (9.9), o tensiune critică de flambaj s_cr (ca raport între forţa critică şi aria secţiunii transversale a barei), ţinând seama de relaţia de definiţie a razei de inerţie                rezultă că:

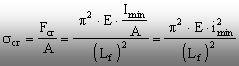                        (9.10)

Această relaţie devine mult mai simplă dacă se face notaţia    (9.11)

   adică                                                                             (9.12)

Se observă că numărul l este obţinut ca raport între două lungimi, deci este adimensional. Trebuie subliniat faptul că acest număr, numit coeficient de subţirime (sau de zvelteţe), este indicatorul principal al modului în care o anumită bară trebuie calculată la flambaj.

În acest sens, pot fi făcute următoarele observaţii:

1. Calculele de stabilitate elastică sunt specifice fiecărei bare concrete, inclusiv în privinţa materialului şi a încărcării ei.

2. Coeficientul l introduce în calculele de flambaj influenţele exercitate asupra stabilităţii barei de lungimea şi rezemarea ei, precum şi de forma şi dimensiunile secţiunii sale transversale.

3. Două bare caracterizate prin aceeaşi valoare a coeficientului de subţirime îşi vor pierde stabilitatea elastică în acelaşi fel.

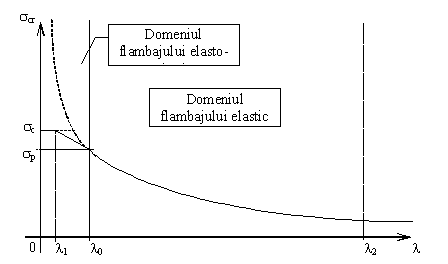
Pornind de la relaţia (9.12), se poate construi o curbă de dependenţă între tensiunea critică de flambaj şi coeficientul l. Principial, graficul acestei funcţii reprezintă o hiperbolă echilateră.

Cum relaţia (9.12) se referă la flambajul elastic, rezultă că partea hiperbolică a graficului (fig. 9.6) se restrânge la zona aflată sub limita de proporţionalitate a materialului (s_cr<s_p). Pentru a delimita această zonă pe axa absciselor, se extrage din relaţia (9.12) valoarea lui l care corespunde tensiunii s_p, astfel:

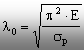                                       (9.13)

Fig. 9.6

Prin urmare, graniţa (l₀) a zonei de aplicabilitate a formulei lui Euler reprezintă o mărime caracteristică pentru materialul barei (de exemplu, pentru oţelurile obişnuite această graniţă se admite a fi l₀@100). Domeniul de pe grafic (fig. 9.6) aflat la dreapta acestei graniţe aparţine flambajului elastic, pe când cel aflat la stânga trebuie să descrie dependenţa dintre tensiunea critică şi coeficientul l în domeniul flambajului elasto-plastic.

Atenţie! Cum pentru fiecare bară şi mod de rezemare corespunde o anumită valoare a lui l, rezultă că oricărei situaţii concrete de încărcare i se poate afla punctul reprezentativ de pe axa absciselor din graficul de mai sus, iar în acest fel se poate stabili modul în care se poate produce pierderea stabilităţii longitudinale a barei.

Trebuie făcută observaţia că valoarea coeficientului l este cu atât mai mare cu cât bara este mai lungă, în raport cu dimensiunile secţiunii transversale (adică cu cât este mai zveltă). Din figura 9.6 se observă că, dacă l creşte foarte mult, domeniul tensiunilor admisibile scade spectaculos, făcând ca bara să nu mai poată fi, practic, încărcată cu forţe de compresiune.

Aceasta face ca domeniul concret al flambajului elastic să fie limitat şi în partea sa dreaptă: astfel, se impune ca barele zvelte să nu aibă un coeficient de subţirime mai mare decât un anume (l₂) care se alege, din literatură, în funcţie de aplicaţia concretă analizată.

Astfel, pentru barele făcute din oţeluri obişnuite, utilizate în construcţii de maşini sau la realizarea construcţiilor metalice, se admite că această limită este l₂ = 200¸250.