Aplicaţii

9.1. Să se calculeze forţa de compresiune pe care o poate suporta o tijă, având lungimea L şi secţiunea transversală de forma şi dimensiunile indicate în figura 9.7, ştiind că este încastrată şi articulată la capete şi solicitată ca în figura 9.5.

    Tija este din oţel, cu modulul de elasticitate E=2,1×10⁵MPa şi are parametrii dimensionali L=0,6m şi t=4mm. Coeficientul de siguranţă la flambaj se consideră a avea valoarea c=4.

Rezolvare

Secţiunea transversală are două axe de simetrie, care sunt şi axele principale centrale de inerţie ale secţiunii, iar momentele principale centrale se calculează astfel:

Observaţii: Pentru momentul faţă de axa z s-a făcut scăderea între momentul secţiunii brute şi al celor două dreptunghiuri “verticale” (3t×6t); faţă de axa y s-a descompus secţiunea în două dreptunghiuri “orizontale” (8t×2t) şi unul vertical – “inima” profilului – (2t×6t).

Observând că momentul minim se obţine faţă de axa y şi că aria secţiunii este A=44t², se poate calcula raza minimă de inerţie, astfel:

Din modul de rezemare rezultă că lungimea de flambaj este L_f=0,707×L; prin urmare, coeficientul de zvelteţe pentru tija analizată este:

Această valoare arată că flambajul barei se va produce în domeniul elasto-plastic, iar tensiunea critică se va calcula cu relaţia (9.14), cu coeficienţii indicaţi la prezentarea relaţiei respective. Dintr-o relaţie de forma (9.1) se extrage formula forţei maxime pe care o poate suporta tija, astfel:

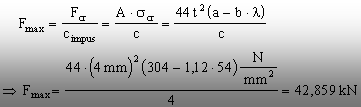
Observaţii:

1. Dacă valoarea coeficientului de zvelteţe ar fi fost mai mare decât 100, atunci forţa critică s-ar fi calculat cu relaţia lui Euler.

2. Se remarcă efectuarea tuturor calculelor sub formă literală, până la obţinerea relaţiei finale, singura în care (cu excepţia determinării lui l) s-au făcut înlocuiri numerice.

9.2. Să se dimensioneze un stâlp vertical, articulat la ambele capete, solicitat într-un mod similar schemei din figura 9.1, ştiind că are secţiunea transversală de formă dreptunghiulară, cu raportul laturilor h/b=2.

Stâlpul este din oţel, cu E =2,1×10⁵MPa şi are lungimea L=0,5m, forţa pe care trebuie să o suporte este F_ef=10⁴N, iar coeficientul de siguranţă la flambaj se impune a fi c=3.

Rezolvare

Coeficientul efectiv de zvelteţe nu poate fi calculat, astfel că se începe raţionamentul făcându-se presupunerea că flambajul stâlpului se produce în domeniul elastic al materialului său (adică l_ef³100).

Pe baza definiţiei (9.1) a coeficientului de siguranţă se poate scrie că F_cr=c×F_ef, iar din relaţia (9.9) se extrage momentul de inerţie minim al secţiunii, sub forma:

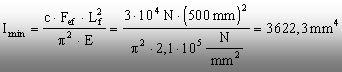
Exprimat în funcţie de dimensiunile secţiunii, cel mai mic dintre momentele de inerţie principale centrale se scrie astfel:

   iar din egalarea celor două valori de mai sus se obţine dimensiunea preliminară a secţiunii stâlpului:

                                                            b = 12,142mm.

Pentru simplitate, se adoptă valoarea rotunjită:

            b = 15mm.

Această valoare ar putea să reprezinte dimensiunea finală a secţiunii, cu condiţia să fie îndeplinită presupunerea iniţială, în legătură cu coeficientul l.

Aria secţiunii transversale este A = 2b², iar raza ei minimă de inerţie va fi

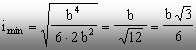
Pe aceste baze, valoarea efectivă a lui l se calculează astfel:

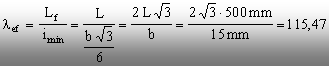
Prin urmare, coeficientul de zvelteţe real este inclus în limitele domeniului flambajului elastic de pe graficul tensiunii critice (fig. 9.6). Presupunerea iniţială a fost corectă, iar dimensionarea barei este valabilă.

Rezultă că secţiunea transversală a barei trebuie să aibă dimensiunile

b=15mm, h=30mm.