Exemplu de calcul

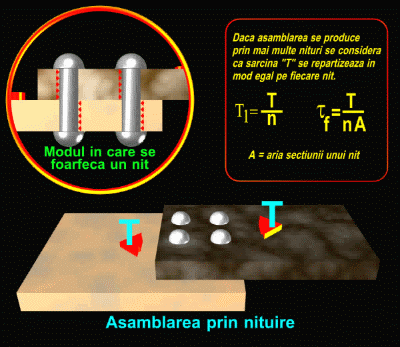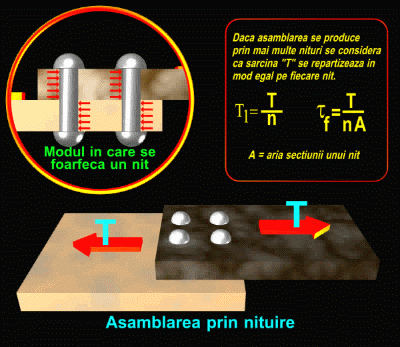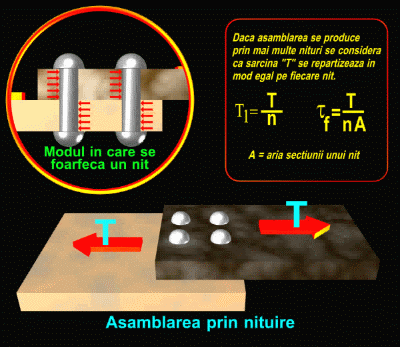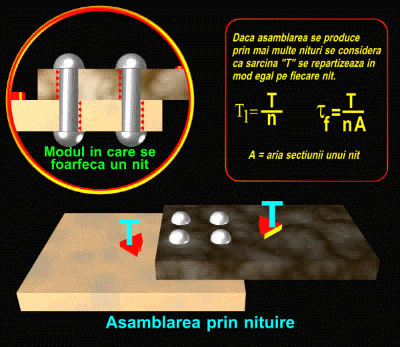
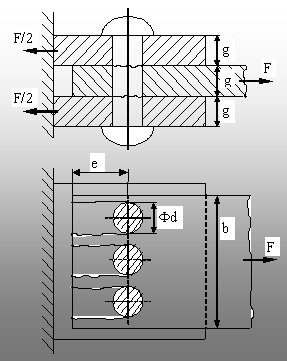
7.4. Să se dimensioneze îmbinarea cu nituri din figura 7.7. Două dintre cele trei foi de tablă sunt fixate (încastrate) pe laturile lor din partea stângă, iar tabla intermediară, prinsă de celelalte prin intermediul a trei nituri, trebuie să preia forţa F. Se cunoaşte forţa F=4×10⁴N, dar şi rezistenţele admisibile s_atb=160MPa, t_atb=120MPa, p_{a str}=180MPa – pentru table,

respectiv t_{a nit}=90MPa – pentru nituri.

Notă: Vederea de sus a fost reprezentată la nivelul feţei superioare a tablei din mijloc, deci cu tabla de deasupra îndepărtată.

Fig. 7.7

Rezolvare

Dacă se analizează reacţi-unile din încastrare, se ob-servă că acestea sunt forţe orizontale, simetrice şi egale cu jumătate din F.

Rezultă că cea mai solici-tată dintre table este cea in-termediară, încărcată cu for-ţă dublă faţă de celelalte.

Prin urmare, toate calcu-lele de rezistenţă referitoare la foile de tablă se vor face pentru tabla din mijloc.

Pe de altă parte, se ob-servă că în îmbinarea abor-dată se produc mai multe tipuri de solicitări simultan. Se recomandă (pentru orice problemă de acest fel) a se gândi rezolvarea prin analiza succesivă a modurilor în care se pot distruge elementele constructive ale îmbinării, dacă una dintre dimensiunile ei ar fi insuficient de mare.

După ce se identifică solicitarea care conduce la efectul respectiv, se scriu relaţiile de calcul corespunzătoare acelei solicitări. Se obţine astfel un sistem de inecuaţii (în număr egal cu al necunoscutelor), pe baza căruia se calculează şi apoi se adoptă valorile efective ale dimensiunilor îmbinării.

Pentru problema de faţă, se începe analiza cu elementele de îmbinare, făcând observaţia că, dacă diametrul lor (d) ar fi mai mic decât cel necesar, ele s-ar rupe pe direcţia suprafeţelor de separaţie dintre table (a se vedea liniile ondulate subţiri de pe desen).

Altfel spus, pentru fiecare nit ar exista două suprafeţe de rupere, paralele între ele şi paralele cu forţa F, cea care produce solicitarea. După cum s-a precizat mai sus, această direcţie a secţiunilor de rupere indică apariţia unei solicitări de forfecare, iar aceasta va trebui luată în considerare pentru calculul niturilor.

Dacă se trece la observarea efectelor unei eventuale dimensionări incorecte a tablelor, se pot remarca următoarele posibilităţi:

· O valoare prea mică a lăţimii (b) a tablei (din mijloc) conduce, la limită, la ruperea ei pe direcţie perpendiculară pe forţa F, ceea ce corespunde unei solicitări de tracţiune. Secţiunea periculoasă va fi cea mai mică dintre secţiunile transversale efective ale tablei (cea care se află pe axa diametrală a celor trei nituri).

· Dacă dimensiunea (e) (distanţa niturilor până la marginea tablei) nu este suficient de mare, atunci se produce, la limită, “sfâşierea” tablei, pe direcţia forţei F, la fiecare extremitate a unui nit. Rezultă că se produce forfecare, pe câte două secţiuni de rupere (marcate cu linii subţiri ondulate pe desen) pentru fiecare dintre nituri.

· Dimensiunea (g) este hotărâtoare pentru rezistenţa tablei la strivire, solicitare care se produce pe suprafeţe semi-cilindrice, la contactul dintre tablă şi nituri (câte o suprafaţă de rupere pentru fiecare nit).

Dimensionarea îmbinării presupune următoarele operaţii:

a) Calculul niturilor la forfecare

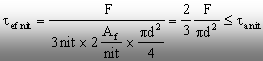
Din ultima relaţie rezultă inecuaţia

(1)

b) Calculul tablelor la tracţiune

De aici rezultă condiţia

(2)

c) Calculul tablelor la forfecare

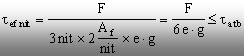
Rezultă că

(3)

d) Calculul tablelor la strivire

S-a dedus din relaţia (5.18) că aria de strivire este, pentru suprafeţele semi-cilindrice, produsul dintre diametrul şi înălţimea cilindrului, adică:

Din ultima inegalitate rezultă

(4)

S-a obţinut în acest fel un sistem de patru inecuaţii cu patru necunoscute, din care se vor obţine valorile necesare ale dimensiunilor îmbinării. Aceste valori se vor rotunji, prin adaos, ţinând seama şi de alte considerente referitoare la aspectul şi la poziţiile reciproce ale elementelor constructive respective.

Din inecuaţia (1) rezultă valoarea minimă a diametrului niturilor:

Pe această bază se adoptă, de exemplu, valoarea d_ad = 10 mm.

Inecuaţia (4) conduce la stabilirea grosimii minime a tablelor:

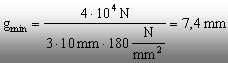
Se poate adopta g_ad = 8 mm.

Introducând aceste valori în inecuaţia (3), rezultă:

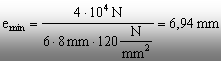
Distanţa obţinută este foarte mică (mai mică decât diametrul nitului), astfel încât se va adopta o valoare de câteva ori mai mare (urmărind, de pildă, indicaţiile dintr-un îndrumar de proiectare), cum ar fi e_ad = 25 mm.

În fine, lăţimea tablelor se va calcula pe baza inecuaţiei (2), astfel:

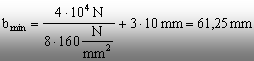
Această valoare a lăţimii este şi ea foarte mică, astfel că dimensiunea efectivă se va putea adopta pe baza altor cerinţe (funcţionale, estetice sau de standardizare dimensională) pe care trebuie să le îndeplinească tablele.