Diferite forme de curbe caracteristice

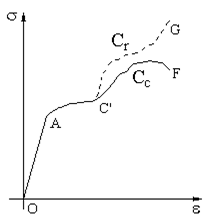
1. Curba caracteristică reală a unui material este diferită, în principiu, de aceea trasată în laborator sau de curba descrisă mai sus. Aceasta este numită curbă convenţională, deoarece ia în considerare, drept mărime plasată în ordonata graficului, nu valoarea teoretică a tensiunii, ci raportul dintre forţa efectivă şi aria iniţială a epruvetei (F/S₀).

Fig. 3.5. Curba caracteristică reală (C_r) şi cea convenţională (C_c).

Dacă s-ar face raportarea la aria “instantanee” a secţiunii transversale, care scade continuu pe parcursul încercării, s-ar obţine curba caracteristică reală, având forma (OCG) (fig. 3.5).

După cum se observă, cele două curbe capătă diferenţe semnificative numai dincolo de limita de curgere a materialului, pe când în aplicaţiile inginereşti este importantă zona iniţială (de proporţionalitate) de pe curba caracteristică.

Prin urmare, trasarea curbei reale nu prezintă un mare interes practic, cu atât mai mult cu cât curba convenţională poate fi obţinută experimental cu relativă uşurinţă, în coordonate (F-DL). În schimb, trebuie să se ţină seama de faptul că rezistenţa la rupere care se determină pe această cale este şi ea o mărime convenţională, care diferă de tensiunea maximă atinsă în epruvetă pe parcursul încercării.

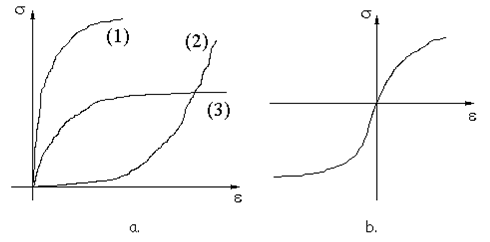
2. Forma curbei caracteristice la tracţiune pentru diverse materiale (fig. 3.6.a) poate fi mult diferită de aceea proprie oţelurilor moi.

Curbe de forma (1) se obţin, de pildă, pentru alamă, beton sau cauciuc, cele de forma (2) – pentru fibrele textile, iar (3) – pentru materiale ductile de tipul cuprului.

Fig. 3.6. Forme de curbe caracteristice la tracţiune (a) şi tracţiune-compresiune (b), pentru diverse materiale utilizate în industrie.

3. Curba caracteristică la compresiune – în cazul oţelurilor uzuale are aceeaşi formă cu diagrama de întindere, deci aproximativ aceleaşi valori pentru mărimile s_p, s_e, s_c şi E. Pentru materialele fragile, cum sunt fontele, este tipic faptul că rezistenţa lor la compresiune este mai mare decât aceea la tracţiune, deci curba caracteristică la compresiune este mai “lungă” decât cea de tracţiune (fig. 3.6.b).

Este interesant de remarcat că, dacă o probă dintr-un material de tipul oţelurilor se supune la compresiune după încercarea ei la întindere şi producerea fenomenului de ecruisare, atunci se constată că limitele de elasticitate şi de curgere s_e şi s_c nu se mai obţin egale cu acelea de la întindere, ci se ating la valori (absolute) mai mici ale tensiunilor (efectul Baushinger).

Trebuie precizat că efectul ecruisării se poate anula, de exemplu, printr-un tratament termic de recoacere aplicat materialului respectiv.

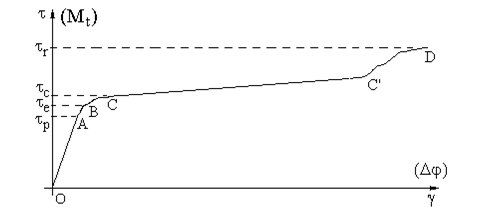
4. Curba caracteristică la răsucire – reprezintă evoluţia dependenţei dintre tensiunile (t) şi lunecările specifice (g) şi este asemănătoare – pentru oţeluri – curbei de tracţiune, dar având zona de curgere mai întinsă (fig. 3.7).

Partea rectilinie iniţială (OA) a curbei are ecuaţia t = G×g (3.7)

care este numită legea lui Hooke pentru solicitarea de răsucire, constanta G fiind modulul de elasticitate transversal al materialului.

Fig. 3.7. Curba caracteristică la răsucire pentru materialele tenace.

După cum rezultă din cele prezentate în acest capitol, proprietăţile materialelor considerate omogene şi izotrope, în domeniul deformării lor de tip elastic (reversibil), sunt concretizate prin trei “constante de elasticitate”: modulul longitudinal E, cel transversal G, respectiv coeficientul contracţiei transversale n. În cadrul teoriei elasticităţii se poate demonstra că între aceste constante există relaţia

(3.8)

ceea ce arată că numai două dintre ele sunt independente.

Observaţie: Pentru materialele neomogene şi anizotrope (cu proprietăţi diferite în direcţii diferite din material), aşa cum sunt în mod tipic materia-lele compozite, numărul constantelor elastice creşte, proporţional cu gradul de anizotropie a proprietăţilor, iar relaţiile dintre constante cresc şi ele în complexitate. Problemele de acest tip nu fac obiectul acestei lucrări, dar rezolvarea lor este prezentată în cărţile care tratează în mod amănunţit teoria elasticităţii, sau studiul proprietăţilor fizico-mecanice ale compozitelor.