Aplicarea teoremelor lui Castigliano la solicitarea de încovoiere

După cum s-a observat anterior, în toate secţiunile transversale ale barelor supuse la încovoiere se produc atât deplasări liniare, cât şi unghiulare. Prin urmare, această solicitare permite aplicarea directă a ambelor teoreme ale lui Castigliano.

Pe o grindă arbitrară se ia în considerare o secţiune transversală cu centrul de greutate în punctul P (aflat pe axa longitudinală a barei) şi în care acţionează sarcinile exterioare concentrate M – de tip moment de încovoiere pe axa (z) şi F – de tip forţă pe direcţia axei (y).

Rotirea j(P) şi deplasarea liniară v(P) ale secţiunii, pe direcţia şi în sensul eforturilor M, respectiv F, se pot calcula, pe baza teoremelor lui Castigliano – relaţiile (4.9) şi (4.10) – şi a expresiei (8.14), astfel:

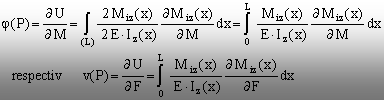(8.15)

Observaţii:

1. S-au calculat derivatele, în raport cu sarcinile M şi F, ale expresiei energiei potenţiale de deformare, ca pentru o funcţie compusă, înainte de efectuarea integralei.

2. Dacă rezultatul unui calcul făcut cu relaţia (8.15) este negativ, înseamnă că respectiva deplasare a secţiunii analizate se produce în sens contrar celui al sarcinii concentrate M sau F.

3. Dacă este necesar să se determine deplasarea unei secţiuni în care nu există sarcina concentrată necesară calculului, atunci teorema se aplică după introducerea, în acea secţiune, a unei sarcini fictive (K), de tipul cerut de algoritmul metodei, urmată de exprimarea tuturor elementelor de calcul (reacţiuni şi eforturi secţionale) în funcţie de această mărime (K).

După efectuarea derivatelor parţiale ale eforturilor M_iz(x) în raport cu (K), se fac înlocuirile necesare în relaţia (8.15), dând încărcării fictive valoarea reală K=0. (A se vedea aplicaţia dintr-un paragraf următor al acestui capitol).