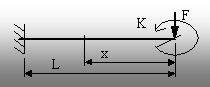
A. Rezolvare pe baza teoremelor lui Castigliano

8.11. Pentru aplicarea teoremelor este necesar ca în secţiunea de calcul să acţioneze sarcini concentrate de tipul precizat, exprimate independent de celelalte încărcări din sistem.

Fig. 8.24

Forţa F satisface această condiţie, iar pentru calculul rotirii capătului barei se introduce un moment fictiv K (de mărime reală zero), alegând să aibă sensul trigonometric (fig. 8.24).

Pe bară există o singură regiune, iar expresia efortului secţional şi derivatele ei parţiale în funcţie de sarcinile considerate vor fi următoarele:

Rotirea şi săgeata capătului liber al barei se vor obţine introducând în relaţia (8.15) termenii corespunzători şi dând apoi sarcinii K valoarea reală (K=0). Rezultă că:

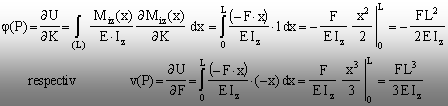
Se observă că aceste valori coincid (cel puţin dacă se face abstracţie de semne) cu cele obţinute în urma aplicării integrării directe a ecuaţiei Euler.

Atenţie: Semnul pozitiv al deplasării liniare arată că aceasta se produce în jos (în sensul lui F), în vreme ce semnul negativ al rotirii indică sensul ei – orar – invers celui al momentului fictiv K!