Aplicarea metodei eforturilor

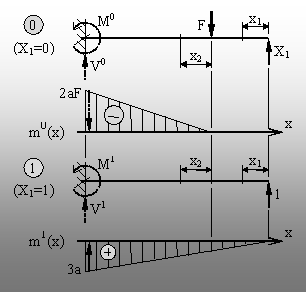
Fig. 8.28

8.15. Algoritmul metodei a fost descris în capitolul al patrulea, iar în cele ce urmează se face aplicarea lui la cazul de solicitare abordat.

Se alege a se transforma sistemul dat într-unul static determinat prin înde-părtarea imaginară a reazemului din dreapta (fig. 8.28), care se înlo-cuieşte prin forţa verticală necunoscută X₁. Cele două stări de solicitare care se vor studia, pentru bara astfel obţinută, vor fi:

· starea “zero” – cu solicitarea exterioară prezentă pe bară şi cu X₁=0;

· starea “1” – cu forţa exterioară îndepărtată şi cu X₁=1.

După cum s-a precizat anterior, pentru aplicarea corectă a metodei este necesar ca împărţirea barei în regiuni să se facă identic în toate stările de solicitare studiate. Eforturile secţionale au următoarea evoluţie pe lungimea barei:

Pentru x₁Î(0; a) m⁰(x₁)=0 m¹(x₁)=1×x=x

Pentru x₂Î(0; 2a) m⁰(x₂)=–F×x m¹(x₂)=1 (a+x)=a+x

Aceste rezultate sunt prezentate şi grafic (fig. 8.28) prin diagramele de momente care corespund celor două stări imaginare (fictive) de solicitare.

Problema abordată este simplu static nedeterminată, astfel încât aplicarea metodei eforturilor va conduce la obţinerea unei singure ecuaţii, având ca necunoscută forţa X₁. Conform formulei de calcul (4.13), dacă i = j = 1, această ecuaţie va avea forma următoare:

(8.21)

iar cei doi coeficienţi se vor calcula după relaţia (8.18), aşa cum se arată în continuare.

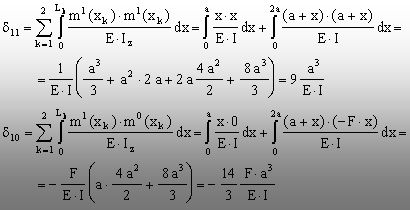
Înlocuind valorile acestor coeficienţi în ecuaţia (8.21), se calculează valoarea forţei necunoscute X₁, care coincide, în fapt, cu reacţiunea V₂ din problema iniţială static nedeterminată.

Rezultă că:

Această soluţie a problemei coincide cu valoarea obţinută prin aplicarea teoremei lui Castigliano, ceea ce confirmă rezolvarea corectă a nedeterminării.