Relaţii diferenţiale între eforturi

Fig. 8.2

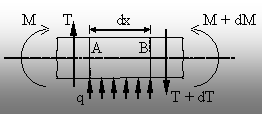
Se izolează un segment, de lungime (dx), dintr-o bară solicitată la încovoiere. Asupra lui se consideră că acţionează o forţă distribuită uniform (deoarece lungimea dx este foarte mică), de intensitate (q), iar eforturile din secţiunile sale de capăt se echivalează cu forţele şi momentele concentrate T şi M – în punctul A, respectiv (T+dT) şi (M+dM) – în punctul B (fig. 8.2). Dacă se analizează echilibrul acestui element de bară, se constată că pot fi scrise două ecuaţii de echilibru semnificative, astfel:

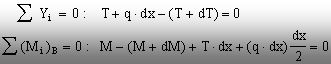
Ultimul termen din cea de-a doua ecuaţie este un “infinit mic de ordin superior”, deci tinde către zero. Pe de altă parte, în ecuaţiile de mai sus se pot reduce termenii asemenea, iar notaţiile eforturilor secţionale, precum şi intensitatea distribuţiei se pot scrie ca funcţii de variabila x, adică de poziţia pe axa longitudinală a elementului de bară studiat. În acest fel se obţin următoarele relaţii diferenţiale între eforturile dintr-o secţiune transversală oarecare a unei bare supuse la încovoiere:

(8.1)

Rezultă că se pot enunţa următoarele două reguli:

à Derivata, în raport cu x, a expresiei matematice a efortului de tip forţă tăietoare T_y(x) reprezintă expresia matematică a forţei distribuite q(x) din secţiunea considerată.

à Derivata, în raport cu x, a expresiei matematice a efortului de tip moment încovoietor M_iz(x) reprezintă expresia matematică a forţei tăietoare T_y(x) din secţiunea considerată.

Este evident că semnul membrului drept din expresiile (8.1) va fi direct influenţat de convenţia de semne definită mai sus. Astfel, dacă se iau în considerare încărcările din partea dreaptă, în raport cu secţiunea de calcul, atunci cele două tipuri de eforturi au convenţii de semne inverse (forţele tăietoare considerate pozitive produc momente de semn negativ faţă de secţiune), iar derivata expresiei momentului va fi egală cu [-T_y(x)].

Pe baza relaţiilor (8.1) pot fi scrise şi câteva consecinţe importante pentru deducerea expresiilor eforturilor secţionale:

1. Între expresiile matematice ale momentului încovoietor şi forţei tăietoare, respectiv între cele ale forţei tăietoare şi forţei distri-buite din orice secţiune transversală a unei bare solicitate la înco-voiere există toate legăturile dintre o funcţie matematică şi deri-vata ei (panta graficului, monotonia funcţiei, puncte de extrem).

Dacă expresiile sunt de tip polinomial, atunci funcţia momentului încovoietor are gradul cu o unitate mai mare decât funcţia forţei tăietoare, iar aceasta din urmă depăşeşte cu o unitate gradul funcţiei de distribuţie a forţei de pe tronsonul de bară considerat.