Tensiuni şi deformaţii specifice

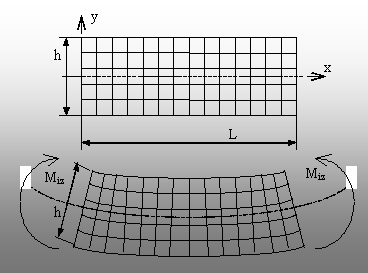
Se consideră o bară prismatică având lungimea L şi înălţimea secţiunii transversale h, pe a cărei suprafaţă se trasează o reţea de linii echidistante, longitudinale şi transversale. Ochiurile reţelei astfel obţinute au formă de pătrate (fig. 8.3).

Dacă la capetele barei se aplică, pe direcţia perpendiculară pe planul desenului, doi vectori moment de mărimi egale şi de sensuri contrare, atunci bara este solicitată la încovoiere, iar prin analiza efectelor acestei solicitări se observă următoarele:

Þ Marginile barei tind să se ridice faţă de mijlocul ei, iar axa longitudinală, precum şi “fibrele” de material paralele cu această axă, capătă forme aproximative de arce de cerc.

Þ Aceste arce au lungimi inegale (cu atât mai mari cu cât se află mai la exteriorul curburii).

Þ Cum volumul de material nu se modifică, rezultă că o parte dintre fibre trebuie să se scurteze, iar altele să se lungească, existând şi unele care nu se deformează.

Fig. 8.3

Þ Se poate spune deci că fibrele din jumătatea superioară a barei sunt solicitate la compresiune, cele din partea de jos sunt supuse la tracţiune (deci tensiunile care apar în bară sunt de tip s(x) – ca la solicitările axiale), iar fibrele din planul median (planul neutru al barei) nu sunt solicitate. Solicitările maxime se produc la extremităţile secţiunilor transversale.

Secţiunile care erau iniţial plane şi perpendiculare pe axa barei îşi păstrează, în principiu, aceste caracteristici, după producerea solicitării, chiar dacă se rotesc în jurul axei lor transversale (z). Rezultă că, în cazul încovoierii simple a barelor prismatice, se poate admite că se respectă ipoteza lui Bernoulli, ceea ce simpli-fică mult calculele de rezistenţă şi de rigiditate la încovoiere.