Deducerea relaţiilor pentru calculele de rezistenţă

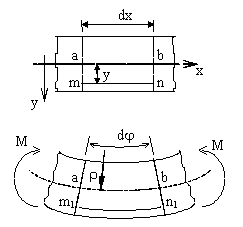
Se consideră un volum elementar, de lungime (dx), dintr-o bară solicitată la încovoiere prin momentele concentrate M (fig. 8.4). În acest volum se evidenţiază fibra longitudinală (mn), situată la distanţa (y) de planul median al barei, în care îi corespunde fibra (ab).

Ca urmare a solicitării, bara se curbează, iar fibra (mn) se alungeşte, ajungând în poziţia (m₁n₁), în timp ce fibra mediană rămâne la aceeaşi lungime

ab = dx = r dj.

Observaţii:

1. Ultimul termen din relaţia de mai sus exprimă lungimea arcului (ab), în funcţie de raza de curbură şi de unghiul la centru care îi corespund.

2. Pentru calculele de la încovoiere este util să se aleagă sensul axei (y) către exteriorul curburii barei îndoite, aşa cum s-a procedat în desenul de mai sus.

Fig. 8.4

Rezultă că lungimea finală a fibrei (mn) poate fi exprimată ca

m₁n₁ = (r+y)dj.

Dacă se calculează alungirea (Ddx) fibrei (mn), se obţine:

Prin urmare, deformaţia specifică a acestei fibre va fi:

,

iar dacă se admite că solicitarea nu depăşeşte limita de elasticitate a materialului, atunci se respectă legea lui Hooke, iar tensiunea din fibra de la distanţa (y) de planul median va fi:

(8.2)

Din această expresie rezultă că tensiunile din fibre, la fel ca deformaţiile specifice ale acestora, sunt direct proporţionale cu distanţa fibrelor până la axa neutră a grinzii, având valoarea maximă de tracţiune în fibra extremă inferioară (unde distanţa y are cea mai mare valoare de semn pozitiv), iar valoarea maximă de compresiune la extremitatea superioară. În plus, mărimile s şi e sunt nule în planul neutru al grinzii (unde y=0).

Pe de altă parte, dacă se admite că raza de curbură este aceeaşi în toate fibrele barei, din relaţia (8.2) rezultă că, pentru barele cu secţiuni transversale simetrice faţă de planul neutru, tensiunile maxime de întindere şi compresiune dintr-o aceeaşi secţiune sunt egale în valoare absolută.

Pentru a se stabili legătura dintre tensiuni şi efortul secţional de tip moment încovoietor, se face apel la ecuaţiile de echivalenţă, prezentate anterior (a se vedea ecuaţiile (1.18) şi figura 1.12), dintre care cea de-a şasea se scrie:

Introducând sub integrală expresia (8.2) a tensiunii şi identificând apoi relaţia (2.5) de definiţie a momentului de inerţie I_z al secţiunii de calcul, se obţine:

(8.3)

În fine, dacă se extrage din (8.3) valoarea fracţiei (E/r), înlocuind-o apoi în membrul drept al expresiei (8.2), se ajunge la relaţia pentru calculul tensiunilor normale efective din fibra (y) a secţiunii arbitrare (x) dintr-o bară solicitată la încovoiere (relaţia lui Navier):

(8.4)

Din analiza acestei relaţii rezultă că:

à Tensiunile de încovoiere sunt direct proporţionale cu momentul încovoietor din secţiunea de calcul M_iz(x) (a cărui valoare se obţine din diagrama de efort) şi cu distanţa (y) a fibrei de calcul până la axa neutră a barei şi invers proporţionale cu momentul de inerţie axial al secţiunii considerate I_z(x).

à Grinda va suporta cu atât mai bine solicitarea cu cât va fi mai mare momentul de inerţie al secţiunii sale transversale, în raport cu axa care reprezintă direcţia vectorului moment încovoietor (axa de îndoire a barei, pentru secţiunea respectivă).

Pentru calculele de rezistenţă este importantă valoarea maximă a tensiunii (care apare în fibrele cele mai distanţate de axa de îndoire) din secţiunea cea mai solicitată a barei, adică:

Dacă, în această relaţie, se trece mărimea (y _max) la numitorul numitorului, atunci se obţine relaţia de definiţie (2.15) a modulului de rezistenţă axial W_z(x). Se deduce astfel relaţia pentru calculele de rezistenţă, în cazul barelor solicitate la încovoiere:

(8.5)

Principial, problemele de încovoiere necesită parcurgerea următoarelor etape:

· Trasarea diagramei momentelor de încovoiere M_iz(x) – pentru stabilirea secţiunilor transversale în care solicitarea este maximă.

· Trasarea diagramei forţelor tăietoare T_y(x) (dacă este necesară!).

· Verificarea corelaţiilor dintre cele două diagrame, dar şi dintre acestea şi încărcările de pe grindă, pe baza relaţiilor diferenţiale între eforturi.

· Particularizarea inecuaţiei (8.5), pentru secţiunea periculoasă a barei.

Efectuarea calculelor cerute de problemă.