Exemple de calcul

Fig. 8.5

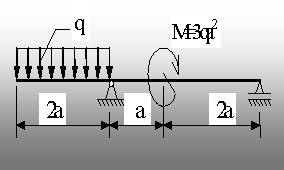
8.1. Să se traseze diagramele de eforturi pentru grinda din figura 8.5.

Rezolvare

a) Calculul reacţiunilor

Se notează cu V₁ reacţiunea verticală din articulaţie, respectiv cu V₂ – cea din reazemul simplu (fig. 8.6), iar cele două ecuaţii de echilibru semnificative se scriu astfel:

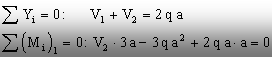
Ecuaţia de momente de mai sus conduce la valoarea reacţiunii din dreapta

V₂ = (1/3)qa.

Cea de-a doua reacţiune se calculează dintr-o altă formă a ecuaţiei de momente:

din care rezultă că V₁ = (5/3)qa.

Verificare: V₁ + V₂ = (1/3)qa + (5/3)qa = 2qa rezultatele sunt corecte.

b) Stabilirea expresiilor analitice ale eforturilor secţionale şi trasarea diagramelor de efort

Punctele în care se aplică încărcările delimitează pe grindă un număr de trei regiuni (fig. 8.6), iar expresiile eforturilor sunt:

Fig. 8.6

Pentru x₁Î(0; 2a)

T_y(x₁)=–q x funcţie liniară T(0)=0; T(2a)=–2qa

M_iz(x₁)=–q x×(x/2) =–(1/2)q x² funcţie de gradul al doilea.

Derivata ei este M’_iz (x₁)=–q x=T_y(x₁).

Această derivată se anulează în x₁=0, care va fi un punct de extrem pentru funcţia M(x₁).

Cum cea de-a doua derivată este M’’_iz (x₁)=–q < 0 rezultă că extremul este un punct de maxim al funcţiei, iar valorile momentului la capetele tronsonului studiat vor fi

M(0)=M_max(x₁)=0; M(2a)=–2qa².

Pentru x₂Î(0; a), alegem să calculăm efectele încărcărilor din partea dreaptă şi rezultă

T_y(x₂) = –V₂ = –(1/3)qa =ct.

M_iz(x₂) = V₂ (2a+x) – M = (1/3)qa (2a+x) – 3qa² =

= (2/3)q a² + (1/3)qa x – 3qa² = – (7/3)qa² + (1/3)qa x

funcţie de gradul întâi, a cărei derivată este

M’(x₂)=(1/3)qa=–T(x₂)=ct.

(derivata momentului şi expresia forţei au semne contrare, datorită convenţiilor inverse de semne, în partea dreaptă faţă de secţiunea de calcul).

Valorile de la capetele regiunii sunt M(x₂=0)=–(7/3) qa²; M(x₂=a)=–2qa².

Pentru x₃Î(0; 2a), calculând tot efectele încărcărilor din partea dreaptă se obţine

T_y(x₃) = – V₂ = – (1/3)qa = ct.

M_iz(x₃) = V₂ x = (1/3)qa x M’(x₃) = (1/3)qa = – T(x₃) = ct.

Valorile de la capetele regiunii sunt M(x₃=0)=0; M(x₃=2a)=(2/3)qa².

Folosind valorile găsite, se trasează diagramele de efort, ca în figura 8.6, cu atenţie la următoarele aspecte:

1. Derivata funcţiei M(x) are aceeaşi valoare în regiunile 2 şi 3, deci pe cele două regiuni graficul va avea o aceeaşi “pantă”!

2. Diagrama de momente de încovoiere se reprezintă cu valorile pozitive sub axa absciselor!!

c) Verificarea corectitudinii diagramelor

Se poate observa că, din relaţiile diferenţiale dintre eforturi (8.1) rezultă, pentru regiunile de pe o bară având încărcare de forţă distribuită uniform (funcţia q(x) de gradul zero), că expresia forţei tăietoare trebuie să fie o funcţie polinomială de gradul întâi (în variabila x), iar cea a momentului încovoietor – de gradul al doilea.

În acelaşi sens, pe regiunile lipsite de forţe distribuite forţele tăietoare nu variază de la o secţiune la alta (funcţie constantă), iar variaţia momentelor se exprimă printr-o funcţie de gradul întâi.

Aceste condiţii sunt îndeplinite de graficele de mai sus, pe care se verifică şi celelalte legături dintre funcţia momentului şi derivata ei – forţa tăietoare:

Þ Derivata este negativă pe toată lungimea grinzii, deci funcţia M(x) trebuie să fie strict descrescătoare peste tot – condiţie îndeplinită dacă se parcurge bara de la stânga către dreapta.

Dacă se alege sensul invers de parcurs, atunci se reaminteşte că, privind către dreapta faţă de secţiunea de calcul, derivata momentului şi forţa tăietoare au semne contrare, adică derivata este pozitivă, iar funcţia – crescătoare.

Þ Secţiunile în care forţa tăietoare este nulă trebuie să corespundă unor valori extreme ale momentului; acest lucru se întâmplă în capătul din stânga al barei, în care funcţia momentelor are un punct de maxim (ceea ce se confirmă fie calculând a doua derivată a funcţiei M(x), fie reamintind sensul descrescător al evoluţiei funcţiei pe lungimea barei).

În fine, este necesar să se verifice concordanţa salturilor din diagrame cu încărcarea grinzii:

Þ pe diagrama de forţe trebuie să existe două salturi – în dreptul reazemelor – ceea ce se şi întâmplă (a se revedea figura 8.6), iar aceste salturi coincid ca valoare şi sens cu reacţiunile V₁ şi V₂;

Þ pe diagrama de momente poate să apară un singur salt, în corespondenţă cu singurul moment concentrat, în valoare de 3qa², care există pe bară.

Observaţie: Şi în privinţa sensului salturilor din diagrama de momente se poate face o legătură cu sensul în care se parcurge, imaginar, grinda.

Astfel, dacă se merge către dreapta – saltul este pozitiv, deoarece momentul M se află la stânga secţiunii de calcul şi corespunde semnului considerat pozitiv în figura 8.1.

Dacă se merge către stânga, atunci momentul are sens negativ, faţă de secţiunea de calcul, deci şi saltul se face de la o valoare pozitivă (2/3 qa²) la una negativă (–7/3 qa²) a efortului.

Se recomandă ca etapa de verificare a diagramelor de eforturi să nu lipsească din rezolvarea problemelor de încovoiere, pentru că toate calculele ulterioare depind de corectitudinea stabilirii expresiilor eforturilor secţionale, respectiv a trasării graficelor acestora.

Fig. 8.7

8.2. Să se traseze diagramele de eforturi pentru grinda din figura 8.7.

Rezolvare

Calculul reacţiunilor a fost efectuat într-un capitol ante-rior (aplicaţia 1.3):

V₁ = (17/6)qa

V₂ = –(7/6)qa

Pe lungimea barei se delimitează patru regiuni (fig. 8.8), iar expresiile eforturilor secţionale se prezintă în continuare.

Pentru x₁Î(0; 3a), încărcarea este distribuită neuniform, iar legea de distribuţie se află prin stabilirea valorii intensităţii q(x) a forţei în secţiunea curentă.

Aplicând cunoştinţe simple de geometrie (asemănări de triunghiuri), se obţine q(x₁)=(2q/3a)x.

Pe baza relaţiilor analitice între eforturile secţionale, rezultă că, pe această regiune a grinzii, forţele tăietoare vor varia după o funcţie parabolică, iar momentele după o funcţie de gradul al treilea. Aceste aspecte vor fi confirmate de calculele bazate pe definiţiile eforturilor.

Dacă ne referim la încărcările aflate la stânga faţă de secţiunea (x₁), se observă o forţă distribuită în formă de triunghi, având catetele (x₁) şi q(x₁). Rezultanta acesteia va fi egală cu aria triunghiului, iar forţa tăietoare din secţiune va fi:

T_y(x₁) = V₁ – q(x₁) x/2 = (17/6) qa – (2q/3a) x²/2 = (17/6) qa – (q/3a) x²

funcţie de gradul al doilea, cu derivatele T’(x₁)=–(2q/3a)x=–q(x₁)

(semnul negativ rezultă din convenţia de semne), T’’(x₁)=–(2q/3a)<0

Prima derivată se anulează în x₁=0, care va reprezenta un punct de maxim al funcţiei (pentru că derivata a doua este negativă). Prin urmare, valorile de la extremităţile regiunii vor fi

T(0) = T_max(x₁) = (17/6) qa; T(3a) = (17/6 – 3) qa = –(1/6) qa

Pentru evoluţia funcţiei momentelor este importantă secţiunea în care forţa tăietoare se anulează, adică punctul

Ţinând seama de modul cum se calculează rezultanta unei forţe distribuite în formă de triunghi, precum şi de poziţia centrului de greutate al încărcării, expresia momentelor încovoietoare se scrie astfel:

adică o funcţie de gradul al treilea în (x), aşa cum era de aşteptat.

Derivata ei este M’ _iz (x₁) = (17/6) qa – (q/3a) x² = T_y(x₁)

Această funcţie a fost studiată complet anterior, ajungându-se la concluzia că în secţiunea (x₁=2,9×a) se înregistrează un punct de extrem pentru M(x₁).

Cum cea de-a doua derivată este negativă (datorită semnului coeficientului din termenul care conţine pe x³), rezultă că extremul este un punct de maxim al funcţiei. Prin urmare, valorile momentului care prezintă importanţă la trasarea graficului vor fi

M(0)=0; M(2,9a)=M _max(x₁)=5,51 qa²; M(3a)=(11/2) qa²=5,5 qa².

Atenţie: Este important de precizat că notarea variabilei (x) cu indici numerici este folosită doar pentru identificarea regiunii pentru care se scrie o anumită expresie a unui efort secţional!

Cu alte cuvinte, oricare astfel de expresie nu poate include simultan două variabile cu indici diferiţi (x_i şi x_j). Din acest motiv, în interiorul expresiilor analitice ale eforturilor nu este nevoie să se pună vreun indice variabilei (pentru că s-ar complica inutil scrierea), aşa cum se observă în relaţiile de mai sus.

Pentru x₂Î(0; 2a), alegem să calculăm efectele încărcărilor din partea stângă şi rezultă

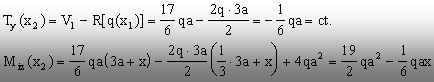
Aceste expresii respectă relaţiile dintre moment şi forţa tăietoare, iar pentru trasarea graficelor este nevoie doar de valorile de capăt ale momentului:

M(0) = 9,5 qa²; M(2a) = (55/6) qa²= 9,17 qa².

Pentru x₃Î(0; a) (cu variabila crescând către stânga!), calculând efectele încărcărilor din partea dreaptă faţă de secţiunea de lucru, se consideră (pentru simplificarea scrierii) că forţa distribuită uniform este alcătuită din două porţiuni distincte – una de lungime (3a), din capătul barei şi până la reazem, cealaltă de lungime (x), din dreptul reazemului şi până la secţiunea arbitrară – şi se obţine

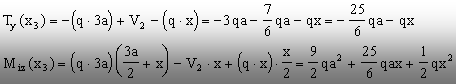
Aceste rezultate confirmă, de asemenea, relaţiile care trebuie să existe între expresiile analitice ale momentelor încovoietoare şi forţelor tăietoare, inclusiv în privinţa semnelor inverse (datorită situării la dreapta faţă de secţiunea de calcul).

Se observă că derivata momentului (expresia forţei tăietoare, cu semnele termenilor inversate) nu poate avea valoarea zero pe acest interval, deci funcţia M(x₃) nu are vreun extrem. Derivata este strict pozitivă, deci funcţia este strict crescătoare, atunci când regiunea este parcursă de la dreapta către stânga, aşa cum s-a considerat aici (a se vedea figura 8.8).

Valorile celor două funcţii la capetele regiunii sunt următoarele:

În fine, pentru x₄Î(0; 3a), calculând efectele încărcărilor din partea mai simplă – cea din dreapta – rezultă

T_y(x₄) = – q x M_iz(x₄) = (q/2) x²

funcţii care sunt foarte simplu de analizat.

Derivata momentului (egală şi de semn contrar cu expresia forţei tăietoare) se anulează în secţiunea (x₄=0), unde se va înregistra un punct de minim al funcţiei, deoarece M’’(x₄)=q>0.

Valorile celor două funcţii ale eforturilor secţionale la capetele regiunii sunt:

T(0)=0; T(3a)=–3qa; M(0)=M _min(x₄)=0; M(3a)=(9/2)qa²

Toate calculele efectuate mai sus conduc la trasarea diagramelor de eforturi din figura 8.8.

Verificarea diagramelor

a) Corespondenţa dintre gradul funcţiilor polinomiale ale eforturilor şi tipul încărcărilor de pe grindă: pentru porţiunea fără forţă distribuită – forţele tăietoare sunt constante, iar momentele se distribuie liniar; pe regiunile cu forţă distribuită uniform – T_y(x) este funcţie liniară (cu aceeaşi pantă pe ambele regiuni, pentru că este o aceeaşi valoare a intensităţii forţei), iar M_iz(x) – parabolică; în fine, în zona cu forţă distribuită liniar – T_y(x) are gradul doi, iar M_iz(x) – gradul trei.

Fig. 8.8

b) Salturile: pe diagrama T(x) trebuie să existe trei salturi (marcate pe desen), care corespund forţelor concentrate, de direcţia axei (y), de pe grindă; diagrama M(x) conţine un singur salt – în dreptul momentului M=4qa², deci graficul trebuie să înceapă şi să se termine în puncte de pe axa absciselor (efortul secţional de tip moment este nul la capetele, neîncărcate cu momente concentrate, ale grinzilor!).

c) Legătura dintre funcţii şi derivatele lor: dacă se parcurge grinda către dreapta, se observă că funcţia M(x) este strict crescătoare, pe porţiunile în care T(x) este pozitivă, respectiv strict descrescătoare, acolo unde T(x) este negativă; în plus, secţiunile în care graficul T(x) trece prin zero (x₁=2,9a şi x₄=0) corespund unor puncte de extrem ale funcţiei M(x); pe prima regiune funcţia liniară q(x) trece prin zero în secţiunea de capăt (x₁=0), care corespunde unui punct de maxim pentru funcţia forţelor tăietoare.

Toate condiţiile de mai sus fiind îndeplinite, se poate spune că diagramele trasate sunt corecte.

Fig. 8.9

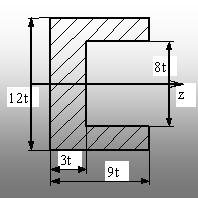
8.3. Să se dimensioneze grinda solicitată ca în figura 8.8 şi având secţiunea transversală de forma şi proporţiile din figura 8.9, cunoscând valorile q=25N/mm; a=0,1m şi s_a=180MPa.

Se observă că secţiunea are drept axă de îndoire axa de simetrie orizontală (z).

Caracteristicile ei în raport cu această axă principală centrală, I_z şi W_z, au fost calculate într-un capitol anterior (a se vedea aplicaţia 2.6 şi figura 2.8):

I_z = 1040 t⁴; W_z = (1040/6) t³

Prin urmare, se poate scrie tensiunea efectivă maximă din secţiunea periculoasă a grinzii (x₂=0) sub forma:

Comparând această valoare, după o relaţie de forma (8.5), cu rezistenţa admisibilă a materialului, rezultă că:

Pe această bază se poate adopta o valoare convenabilă a parametrului (t) al secţiunii, de exemplu t_ad=5 mm. Rezultă o secţiunea transversală a grinzii cu dimensiunile de gabarit (45´60) mm.