Bare de egală rezistenţă la încovoiere

Din cele prezentate anterior a rezultat că tensiunile de încovoiere sunt repartizate neuniform pe secţiunile transversale ale grinzilor, solicitările maxime apărând în fibrele cele mai distanţate de axa de îndoire (z). Acest fapt este exprimat şi de relaţia lui Navier (8.4), care arată că valoarea tensiunilor este direct proporţională cu distanţa (y) a fibrei de calcul până la planul neutru al grinzii.

De aici rezultă că, pentru ca materialul să fie utilizat raţional, lăţimea secţiunii trebuie să fie mai mare, la extremităţile ei, decât în preajma axei neutre. Astfel, grinzile din profile laminate de tip “I” sau “U” sunt mai avantajoase decât cele de secţiune dreptunghiulară sau circulară.

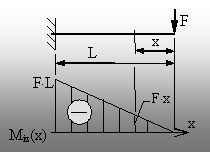
Fig. 8.10

Pe de altă parte, dacă se analizează, de exemplu, solicitarea unei grinzi în con-solă printr-o forţă concentrată aplicată pe capătul ei liber (fig. 8.10), se observă că eforturile secţionale de tip moment înco-voietor variază liniar pe lungimea barei, având valoarea maximă în încastrare. Pe baza acestei valori a momentului se face calculul de rezistenţă al barei.

Prin urmare, dacă secţiunea transversală este constantă pe întreaga bară, atunci materialul este folosit la capacitatea lui maximă numai în dreptul reazemului, celelalte secţiuni fiind supradimensionate. Pentru a creşte eficienţa construcţiei, ar trebui să se adapteze mărimea secţiunilor transversale la nivelul solicitării care le corespunde.

Cu alte cuvinte, dacă se urmăreşte ca nivelul tensiunilor maxime de încovoiere să fie acelaşi în toate secţiunile grinzii, adică s_efmax(x)=ct.=s₀, cum momentul este variabil de la o secţiune la alta, din relaţia (8.7) rezultă că modulul de rezistenţă al secţiunilor transversale trebuie să fie şi el variabil, după o funcţie de forma

(8.8)

O asemenea grindă se numeşte bară de egală rezistenţă la încovoiere, iar relaţia de mai sus arată că forma ei depinde de încărcarea şi modul de rezemare ale barei, dar şi de tipul de secţiune transversală care se utilizează.

Pentru bara din figura 8.10, în cazul în care se adoptă secţiunea dreptunghiulară de lăţime (b) şi înălţime (h), construcţia de eficienţă maximă poate fi realizată în două variante distincte, după dimensiunea care se alege să fie variabilă pe lungimea grinzii.

A. Cazul grinzii de lăţime variabilă b(x)

Folosind relaţia (2.20) pentru calculul modulului de rezistenţă, ecuaţia (8.8) devine:

de unde rezultă funcţia de variaţie a lăţimii grinzii, sub forma

(8.9)

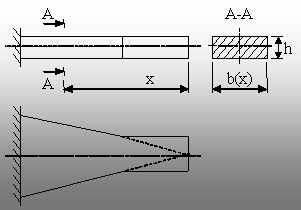
Fig. 8.11

adică această dimensiune variază liniar pe lungimea barei.

Practic, grinda poate fi simetrică (fig. 8.11) sau nesimetrică, iar porţiunea de la capătul liber nu este ascu-ţită (nu porneşte de la lăţime nulă), deoarece trebuie să suporte efortul de tip forţă tăietoare T_y(x)=ct.=F.

Altfel spus, partea de lăţime constantă de la capătul grinzii se dimensionează din considerente de rezistenţă la forfecare.

B. Cazul grinzii de înălţime variabilă h(x)

Relaţia (8.8) se scrie sub forma

care conduce la variaţia înălţimii după relaţia

(8.10)

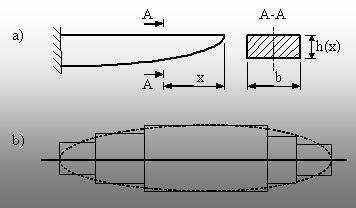
Fig. 8.12

adică o evoluţie parabolică. La fel ca în cazul precedent, grinda poate fi construită simetric (sub formă de parabolă bilaterală) sau nesimetric (ca în figura 8.12 - a).

Un caz particular de grindă de egală rezistenţă este cel al arborilor de transmisie. Realizarea lor practică se bazează pe aproximarea profilului parabolic prin trepte cilindrice de diametre diferite (fig. 8.12 - b).