Calculul tensiunilor tangenţiale din barele solicitate la încovoiere

Dacă se urmăreşte modul în care se curbează, în urma solicitării de încovoiere, o grindă compusă din mai multe plăci prismatice identice, suprapuse (de forma unor scânduri), se observă că suprafeţele frontale de la capetele plăcilor curbate nu se găsesc în acelaşi plan, aşa cum se întâmpla în starea nedeformată a ansamblului.

Rezultă de aici că se produc lunecări ale plăcilor, pe suprafeţele de separaţie, ceea ce nu se poate întâmpla decât sub acţiunea unor tensiuni de tip tangenţial apărute, pe direcţie longitudinală, pe acele suprafeţe.

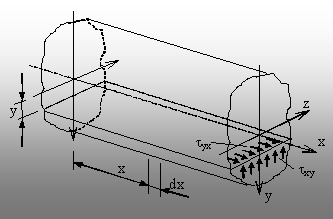
Se consideră un tronson, de secţiune transversală constantă pe toată lungimea, izolat dintr-o bară supusă la încovoiere. Se presupune adevărată ipoteza făcută de Juravski precum că, într-o secţiune longitudinală orizon-tală, situată la distanţa (y) de planul neutru al grinzii (fig. 8.13), tensiunile tangenţiale (t_yx) sunt constante pe întreaga suprafaţă a secţiunii.

Fig. 8.13

Cu alte cuvinte, tensiunile (t_yx) depind numai de coordonata (y) a unui punct de calcul (fiind independente de poziţia punctului pe axele x şi z).

Pe de altă parte, în conformitate cu principiul dualităţii tensiunilor tangenţiale (a se vedea primul capi-tol, fig. 1.12), tensiu-nilor de mai sus le corespund, în secţiunile transversale ale barei, tensiunile tangenţiale (t_xy) având aceeaşi valoare şi aceeaşi orientare faţă de muchia comună (fig. 8.13).

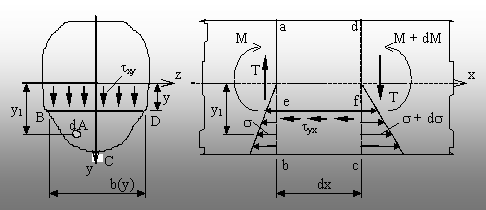
Se propune a se stabili o relaţie de legătură între eforturile din grindă şi tensiunile tangenţiale din “fibra” definită prin coordonata (y). În acest scop, se studiază echilibrul părţii aflate sub fibra (y) a elementului de volum de lungime (dx). Tensiunile şi eforturile secţionale de pe feţele elementului sunt reprezentate schematic în figura 8.14.

Fig. 8.14

Se pot evidenţia mai multe elemente caracteristice ale stării de solicitare analizate.

Astfel, pe secţiunea transversală (a e b), în punctele situate la distanţa (y₁) de planul neutru, tensiunile normale (s) se vor calcula cu o relaţie de forma (8.4), adică

aşa încât se poate vorbi despre o forţă rezultantă, de direcţie axială, care acţionează pe faţa din stânga a elementului de volum considerat şi care se poate determina cu relaţia

În penultimul termen al şirului de egalităţi a fost identificată şi s-a notat prin S _z(y) o integrală de forma (2.2), reprezentând, prin definiţie, momentul static al ariei (BCD) în raport cu axa (z) a secţiunii.

Pe secţiunea transversală (d f c) tensiunea corespunzătoare lui s(y₁) este

iar forţa axială rezultantă de pe faţa din dreapta a volumului elementar se scrie

Dacă se ţine seama şi de forţa rezultantă datorată tensiunilor tangenţiale (t_xy) ce apar pe faţa superioară a elementului de volum, atunci echilibrul forţelor de direcţie axială care acţionează asupra lui se poate exprima sub forma:

Prin înlocuirea termenilor plasaţi între paranteze drepte cu valorile lor de mai sus se ajunge, după reducerea termenilor asemenea, la egalitatea

Din relaţia (8.1) se ştie că (dM/dx)=T(x), deci se poate stabili relaţia căutată (în care se evidenţiază că forţa tăietoare şi momentul de inerţie depind de secţiunea de lucru) pentru calculul tensiunilor tangenţiale din fibra (y):

(8.11)

Numită şi formula lui Juravski, egalitatea de mai sus arată dependenţa tensiunilor tangenţiale de următoarele mărimi:

§ T_y(x)=efortul de tip forţă tăietoare din secţiunea transversală (x) în care se face calculul; dacă diagramele de efort au fost trasate în prealabil, atunci această valoare se extrage din diagramă.

§ b(y)=lăţimea secţiunii, în dreptul fibrei (y) în care se calculează tensiunile (t).

§ I_z(x)=momentul de inerţie, în raport cu axa principală centrală (z) (care este şi axa de încovoiere), al întregii secţiuni transversale.

§ S_z(y)=momentul static, în raport cu axa (z), al părţii din secţiunea (x) care se află deasupra (sau dedesubtul) fibrei (y); este vorba, prin urmare, despre partea din secţiune care lunecă pe fibra de calcul, sub acţiunea tensiunilor tangenţiale t_xy.

Această formulă este utilizată în mai multe categorii de probleme din rezistenţa materialelor, aşa cum se va arăta în continuare.