A. Variaţia tensiunilor tangenţiale pe înălţimea unor secţiuni particulare

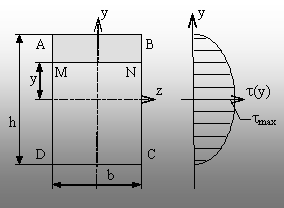
8.4. Cazul secţiunii dreptunghiulare (fig. 8.15)

Se propune a se calcula valoarea tensiunii tangenţiale din fibra orizontală MN a secţiunii dreptunghiulare ABCD. Fibra se află la distanţa (y) de axa neutră a secţiunii, iar lăţimea ei nu depinde de această distanţă: b(y)=ct.=b.

Dacă se consideră că se studiază o grindă solicitată ca în figura 8.10, atunci efortul forţă tăietoare este constant pe lungimea barei: T_y(x)=ct.=F

Fig. 8.15

Secţiunea dreptunghiulară a fost analizată anterior (aplicaţia 2.1) în privinţa momentelor de iner-ţie principale centrale, deci se cunoaşte că: I_z = (b×h³)/12.

În acest fel, dintre mărimile ce apar în relaţia (8.11) a rămas de determinat doar momentul static al părţii din secţiune care lunecă pe fibra MN. Alegându-se partea de deasupra fibrei (aria ABNM, al cărei centru de greutate se notează G₁) şi folosind relaţia (2.2) – definirea momentului static, se obţine:

Prin înlocuirea valorilor de mai sus în relaţia (8.11), se obţine expresia tensiunilor tangenţiale din fibra de calcul, astfel:

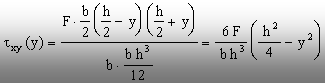
Din această expresie, precum şi din modul în care a fost obţinută, rezultă următoarele:

Þ Dacă forţa tăietoare şi forma secţiunilor transversale nu variază pe lungimea barei, atunci tensiunile tangenţiale depind numai de coordonata (y) a fibrei de calcul.

Þ Dacă lăţimea secţiunii este constantă, măcar pe porţiuni din înălţimea ei, atunci funcţia de variaţie a tensiunilor tangenţiale în raport cu (y) va fi aceeaşi cu a momentului static S_z(y) (înmulţită cu nişte mărimi constante).

Þ Funcţia tensiunilor tangenţiale de pe secţiunea dreptunghiulară se reprezintă grafic sub formă de parabolă, având rădăcinile în punctele simetrice y=–h/2 şi y=h/2 (a se vedea prima formă a expresiei de mai sus, în care funcţia de gradul doi apare scrisă “cu rădăcinile separate”). Vârful parabolei (mijlocul distanţei dintre rădăcini) se va găsi în punctul y=0 (adică exact pe axa neutră, la încovoiere, a secţiunii).

Þ Valoarea maximă a tensiunilor tangenţiale va fi

Se observă că numitorul ultimei fracţii reprezintă chiar aria secţiunii dreptunghiulare, adică valoarea extremă a lui t este cu 50% mai mare decât valoarea aproximativă (t=F/A) care se introduce în calculele convenţionale la solicitarea de forfecare. Totuşi, acele calcule rămân acceptabile pentru elementele de îmbinare (de exemplu penele longitudinale), care de obicei sunt caracterizate prin dimensiuni relativ mici ale secţiunilor de forfecare.

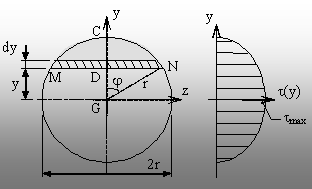
8.5. Cazul secţiunilor circulare pline (fig. 8.16)

Se face referire la fibra MN = b(y), aflată la distanţa (y) de axa neutră (z) a secţiunii. Forţa tăietoare se consideră, ca în cazul precedent, T_y(x)=ct.=F.

Fig. 8.16

Momentul de inerţie prin-cipal central I_z al secţiunii a fost calculat anterior, obţi-nându-se relaţia (2.22) de la aplicaţia 2.2, din care:

Calculul analitic următor necesită exprimarea tuturor dimensiunilor în funcţie de raza (r) a cercului şi de jumătatea (j) a unghiului la centru care corespunde coardei MN.

Prin urmare, dând coordonatei (y) o creştere infinit mică (dy), elementele de calcul necesare pentru definirea elementului de arie (dA) (aproximat printr-un dreptunghi curbiliniu) se vor scrie astfel:

y=r×cosj; dy=–r×sinj dj; b(y)=MN=2 MD=2 r×sinj

dA=b(y)×dy=–2 r²×sin²j dj

Prin urmare, momentul static faţă de axa (z) al părţii din secţiune care lunecă pe fibra MN (alegem din nou partea de deasupra fibrei, adică aria CMDN) se va calcula, conform relaţiei de definiţie (2.2), astfel:

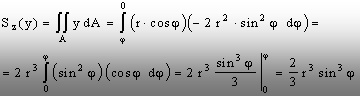
Introducând rezultatele de mai sus în relaţia (8.11), se obţine expresia analitică (de această dată în funcţie de variabila unghiulară j) a tensiunilor tangenţiale din fibra de calcul, sub forma următoare:

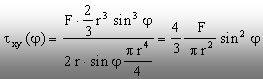
Cum parcurgerea întregii secţiuni se face atunci când unghiul (j) are valori în intervalul [0; p], iar funcţia reprezintă pătratul unei sinusoide, rezultă variaţia tensiunilor tangenţiale după graficul din figura 8.16.

Valoarea lor maximă se înregistrează în fibra de pe axa neutră a secţiunii (în care j=p/2), adică:

La numitorul ultimei fracţii se recunoaşte relaţia de calcul pentru aria cercului de rază r, deci valoarea extremă a lui t este cu o treime mai mare decât valoarea aproximativă (t=F/A) luată în considerare la calculele convenţionale de forfecare. Totuşi, aceste calcule sunt admise pentru piesele de dimensiuni mici (cum sunt niturile sau şuruburile).

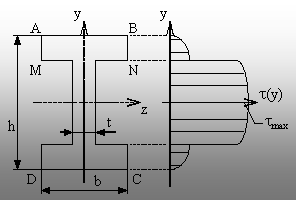
8.6. Cazul secţiunilor de forma literei I (fig. 8.17)

Fig. 8.17

Secţiunile de acest fel aproximează profilele laminate (bare cu secţiuni optimizate pentru preluarea solicitării de încovoiere, având forma literelor I, U, T sau L), pentru care calculul tensiunilor tangenţiale se bazează pe raţionamente precum cel de mai jos.

Secţiunile sunt formate din mai multe dreptunghiuri, deci variaţia lui (t_xy) va fi similară celei de la aplicaţia 8.4. Deosebirea principală provine din variaţia bruscă a lăţimii b(y) a secţiunii, în dreptul fibrei orizontale MN, de la valoarea (b) – la extremităţi (“tălpi”), la valoarea (t) – în zona de mijloc (numită “inima” profilului).

De aici rezultă, pe de o parte, că momentul static S _z(y) va avea un salt în acea fibră. Pe de altă parte, cum valoarea b(y) apare la numitorul relaţiei (8.11), rezultă că trecerea de la talpa la inima profilului conduce la o creştere bruscă a valorii tensiunilor tangenţiale, aşa cum se arată în figura 8.17. Valorile concrete sunt dependente de dimensiunile reale ale secţiunii studiate.

Concluzii

1. Tensiunile de forfecare nu se repartizează uniform pe secţiunile transversale ale barelor solicitate la încovoiere, iar valorile lor maxime depăşesc pe aceea (F/A) luată în considerare în cazul calculelor convenţionale ale elementelor de îmbinare.

Valorile maxime ale tensiunilor tangenţiale t_xy se produc la jumătatea înălţimii secţiunilor transversale. Trebuie observat că, pentru toate secţiunile la care axa de îndoire este axă de simetrie, deci şi axă neutră pentru încovoiere, tensiunile normale s sunt nule pe această axă. Pe de altă parte, tensiunile normale sunt maxime la extremităţile secţiunilor transversale, acolo unde tensiunile t_xy au valoarea zero. Prin urmare, cele două tipuri de tensiuni nu se influenţează reciproc în punctele de pe secţiune în care au valori extreme!