C. Lunecarea longitudinală şi împiedicarea ei

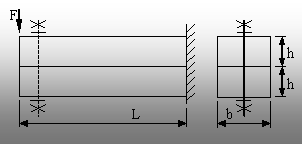
Fig. 8.19

8.8. Bara din figura 8.19 este formată din două grinzi suprapuse, identice, de secţiune dreptunghiu-lară. Acestea pot să parti-cipe la preluarea solicitării în mod independent, sau pot fi solidarizate printr-un bolţ (element de îmbinare cu aspectul unui şurub alungit şi având filetate doar porţiunile de la capete) de diametru (d) (reprezentat simbolic pe desen).

Se cere să se compare capacitatea de rezistenţă a barei, în cele două variante, iar apoi să se stabilească relaţia cu care se calculează diametrul bolţului folosit la îmbinarea grinzilor.

Rezolvare

În cazul în care cele două grinzi nu ar fi solidarizate între ele, atunci măsura rezistenţei lor la încovoiere ar fi dublul modulului de rezistenţă al uneia, adică:

Asamblarea prin intermediul bulonului implică realizarea unei grinzi unice (din punctul de vedere al preluării solicitării de încovoiere), având capacitatea de rezistenţă:

Prin urmare, această măsură dublează rezistenţa la încovoiere (momentul maxim care poate fi preluat) pentru ansamblul analizat.

Pentru calculul de rezistenţă al bulonului, se face mai întâi observaţia că forţa care îl solicită este aceea care face grinzile să alunece una pe suprafaţa celeilalte, în lipsa îmbinării. Această forţă (numită de obicei forţă de lunecare şi notată F_L) este, în fapt, efectul tensiunilor tangenţiale de încovoiere (t_xy) care apar pe suprafaţa de separaţie (a cărei arie este produsul dintre lăţimea b şi lungimea L a grinzilor), adică:

.

Dacă se ţine seama că fibra de calcul se găseşte la jumătatea înălţimii (y=0) unei grinzi de secţiune dreptunghiulară, rezultă, conform relaţie (8.11) – cu momentul static calculat după relaţia de definiţie (2.2) – că:

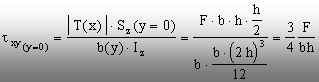
Observaţie: Cum aria secţiunii compuse este (2bh), înseamnă că acest rezultat confirmă valoarea maximă a tensiunilor tangenţiale care s-a calculat în cadrul aplicaţiei 8.4.

Elementul de îmbinare este solicitat la forfecare, iar dacă se consideră că rezistenţa admisibilă a materialului bolţului este (t_ab), atunci relaţia (7.1) devine:

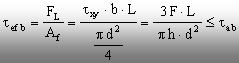
Pe această bază, calculul diametrului bolţului se face astfel:

Se remarcă faptul că dimensiunea bolţului nu este influenţată de lăţimea (b) a grinzilor!

Aplicaţie numerică: Să se stabilească diametrul bolţului folosit pentru îmbinarea a două grinzi, făcute din oţel cu t_a=120MPa şi având dimen-siunile h=50mm, L=0,5m. Ansamblul trebuie să suporte forţa F=3×10⁴N.

Prin înlocuirea acestor valori în relaţia de mai sus se obţine:

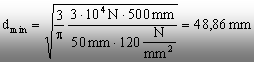
Rezultă că îmbinarea se poate realiza, de exemplu, cu un bulon cu diametrul de 50 mm.

Alte variante ale problemei

În cazul în care sunt solidarizate mai mult decât două grinzi, calculele se vor modifica numai în privinţa tensiunii tangenţiale de pe suprafeţele de separaţie. Din graficul variaţiei lui t_xy pe înălţimea secţiunii globale (fig. 8.15) rezultă că, dacă grinzile sunt în număr impar, atunci tensiunile tangenţiale cele mai mari se vor înregistra pe suprafeţele de lunecare alăturate grinzii din mijloc.

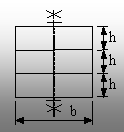
Fig. 8.20

Dacă se îmbină un număr par de grinzi, atunci forţa maximă de lunecare se va produce pe suprafaţa mediană a grinzii finale (la mijlocul înălţimii secţiunilor transversale).

De exemplu, dacă se folosesc trei grinzi ele-mentare (fig. 8.20), atunci tensiunile maxime de lune-care (egale pe ambele suprafeţe de separaţie dintre grinzi) se vor calcula pe fibrele aflate la distanţa (h/2) de axa neutră globală, astfel:

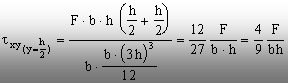
Celelalte calcule se vor face în acelaşi mod ca mai sus.

O altă variantă a acestei probleme o reprezintă cazul folosirii a mai multe buloane, montate la distanţe egale de-a lungul grinzii. În această situaţie, singura modificare a calculelor se referă la suprafaţa de lunecare (implicit – la forţa de forfecare) care corespunde fiecărui bulon. Astfel, dacă sunt (n) buloane, atunci forţa care solicită un bulon va fi:

Există şi alte variante de îmbinări pentru care calculele de rezistenţă implică luarea în considerare a unor forţe de lunecare. Aplicaţia următoare se referă la asamblarea prin sudură a unei grinzi compuse.

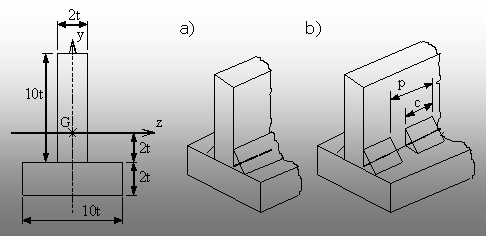
8.9. O grindă cu secţiunea în forma literei T se realizează prin îmbinarea cu sudură (de colţ) a două platbande identice (fig. 8.21), cu dimensiunile transversale (10t´2t). Dacă grinda este solicitată ca în figura 8.10 de mai sus, să se deducă relaţia de dimensionare a cordoanelor de sudură, în cele două variante constructive: a) cordon continuu; b) cordon intermitent.

Fig. 8.21

Rezolvare

Forţa de lunecare preluată de sudură se calculează pe baza valorii tensiunilor tangenţiale de încovoiere care apar pe suprafaţa de separaţie dintre cele două platbande. Pentru aplicarea relaţiei (8.11) este nevoie de cunoaşterea poziţiei pe axa (y) a centrului de greutate global G al secţiunii finale, iar apoi de aflarea momentului de inerţie principal central, al întregii secţiuni, în raport cu axa de îndoire (z).

Dacă se ia în considerare o axă orizontală iniţială situată la baza secţiunii, centrele de greutate ale secţiunilor celor două platbande au coordonatele pe axa (y) de valori y₁=t (pentru platbanda inferioară), respectiv y₂=7t astfel încât, folosind relaţia (2.4), coordonata centrului de greutate global se stabileşte astfel:

Prin urmare, axa (z) a secţiunii globale are poziţia arătată în figura 8.21, iar momentul static faţă de această axă al părţii de secţiune care lunecă pe fibra de calcul se poate determina, folosind relaţia de definiţie (2.2), în două moduri:

· pentru platbanda verticală (partea din secţiune aflată deasupra fibrei), sub forma

· pentru platbanda orizontală (partea de dedesubtul fibrei)

Se poate observa că valoarea acestui moment static este aceeaşi în ambele variante de calcul, ceea ce confirmă precizarea făcută în paragraful anterior, privind explicitarea mărimilor care apar în formula lui Juravski (8.11).

În fine, momentul principal central I_z al secţiunii globale se calculează, folosind relaţiile lui Steiner (2.9), astfel:

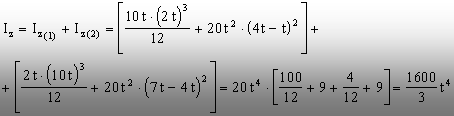
Prin urmare, având în vedere că bara este încărcată ca în figura 8.10 (deci forţa tăietoare este constantă, la valoarea F, pe lungimea grinzii) şi că suprafaţa pe care se face lunecarea are lăţimea (2t), tensiunea tangenţială de pe acea suprafaţă se determină, conform relaţiei (8.11), sub forma:

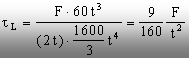
Pe de altă parte, calculul efectiv al cordonului de sudură se face, urmând raţionamentul prezentat la aplicaţia 7.1, în mod diferit pentru cele două variante tehnologice.

a) Cazul cordonului continuu

Forţa de lunecare pe care trebuie să o suporte cele două cordoane de sudură (fiind vorba despre o sudură bilaterală) se referă la întreaga suprafaţă de separaţie, de lungime L, dintre platbande, iar aria totală de forfecare rezultă din luarea în considerare a cordoanelor întregi. Astfel, forţa de lunecare este

F_L = t_L × 2t × L

iar dacă înălţimea secţiunii transversale a cordoanelor se notează cu (a), atunci aria de forfecare va fi

A_f = 2a × L

Prin urmare, calculul de rezistenţă al cordoanelor se face cu relaţia:

b) Cazul cordonului intermitent

De această dată calculul se face pentru o porţiune de grindă de lungimea unui “pas” (p) al sudurii, căreia îi corespunde o lungime efectivă (c) a cordoanelor. Prin urmare, forţa de lunecare ce trebuie preluată pe această porţiune va fi

F_L = t_L × 2t × p

în timp ce aria de forfecare a cordoanelor este

A = 2a × c

Relaţia pentru calculul cordoanelor se va scrie:

Ca principiu, această relaţie permite stabilirea dimensiunii (a) (grosimea electrodului de sudură), dacă se impune (sau se alege) o valoare a raportului (p/c), sau invers. În final, se adoptă unul dintre parametrii cordoanelor (p sau c) şi se calculează celălalt.