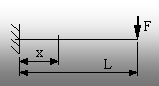
Fig. 8.23

Aplicaţie

8.10. Să se determine expresiile funcţiilor deplasărilor pentru grinda din figura 8.23. Pe această bază, să se precizeze secţiunile în care se obţin valorile maxime ale celor două feluri de deplasări, apoi să se calculeze aceste valori.

Rezolvare

Se observă că expresia momentelor încovoietoare secţionale este aceeaşi pe întreaga lungime a barei, cu alte cuvinte se poate scrie că:

(V) x = (0; L) M_iz(x) = -F (L - x)

iar ecuaţia (8.12) are forma următoare:

Prima operaţie de integrare nedefinită conduce (ţinând seama că secţiunea transversală nu se modifică, pe întreaga bară, deci I_z=ct) la expresia funcţiei de variaţie pe axa barei a rotirilor secţiunilor transversale, astfel:

Aplicând cea de-a doua operaţie de integrare se obţine expresia analitică a deplasărilor liniare:

Condiţiile pentru calculul constantelor de integrare rezultă numai din rezemarea barei (pentru că nu există mai multe regiuni, deci nici condiţii de continuitate), adică din faptul că bara nu poate să se rotească şi nici să se deplaseze, în secţiunea fixată în reazemul încastrat (unde x=0).

Punând aceste condiţii în cele două relaţii de mai sus, se ajunge la valorile C₁=C₂=0, adică expresiile efective ale variaţiei deplasărilor sunt:

Dacă se analizează modul în care se produce deformarea barei, se poate observa că deplasările maxime se înregistrează în capătul liber, adică în punctul în care acţionează forţa concentrată F.

Dacă se introduce, în expresiile de mai sus, valoarea x=L, rezultă aceste valori maxime, astfel:

Observaţie: Prin înlocuirea, în aceste relaţii, a unităţilor de măsură ale mărimilor respective, se evidenţiază faptul că rotirile secţiunilor transversale se măsoară în radiani, iar deplasările liniare – în unităţi de lungime.

Valorile maxime ale deplasărilor înregistrate pe bara analizată vor fi verificate, în cele ce urmează, prin aplicarea unora dintre metodele energetice pentru calculul deformaţiilor barelor solicitate la încovoiere.