Principiul dualităţii tensiunilor tangenţiale

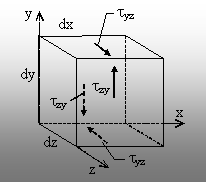
Fig. 1.13.

Se consideră un paralelipiped elementar (de laturi dx, dy şi dz) din interiorul unui corp solid solicitat într-un mod oarecare (fig. 1.13), astfel încât pe feţele sale perpendiculare pe planul (yOz) apar tensiunile tangenţiale t_yz şi t_zy.

După cum s-a arătat mai sus, se poate considera că aceste tensiuni produc efecte similare unor forţe, obţinute prin înmulţirea lor cu ariile suprafeţelor pe care se plasează.

Studiul echilibrului acestor forţe în raport cu sistemul de axe considerat conduce la scrierea unei singure ecuaţii de echilibru semnificative – ecuaţia momentelor faţă de axa (x):

t_yz×(dx dz)dy - t_zy×(dx dy)dz = 0 (1.19)

După cum se observă, din această ecuaţie se obţine egalitatea t_yz = t_zy , care poate fi exprimată, la modul general, astfel:

Existenţa tensiunilor tangenţiale (t_zy) într-un plan oarecare dintr-un corp solicitat implică apariţia unor tensiuni egale (t_yz) într-un plan perpendicular pe primul şi pe direcţia tensiunilor (t_zy). Aceste perechi de tensiuni tangenţiale au orientare simetrică faţă de muchia comună a celor două plane.

Acest enunţ reprezintă principiul dualităţii tensiunilor tangenţiale, iar existenţa lui simplifică mult calculele în cazul solicitărilor la care predomină această categorie de tensiuni.