Deplasări şi deformaţii

În prezentul paragraf sunt introduse două noţiuni de primă importanţă în studiul rezistenţei materialelor, legate în mod direct de considerarea solidelor drept deformabile.

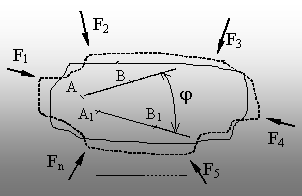
Fig. 1.14

Pentru definirea acestor noţiuni se poate analiza situaţia punctelor din interiorul unui corp de formă arbitrară, solicitat într-un mod oarecare (fig. 1.14). Liniile punctate se referă la situaţia dinainte de producerea solicitării, iar liniile continue – la corpul deformat în urma aplicării solicitării.

Se numesc deplasări schimbările poziţiei punctelor unui corp solid, ca urmare a deformării lui sub o solicitare oarecare. Pot fi:

Þ deplasări liniare – distanţele (AA₁) sau (BB₁) dintre poziţiile ocupate de punctele respective înainte şi după producerea deformării;

Þ deplasări unghiulare (rotiri) – unghiul dintre segmentele de dreaptă (AB) şi (A₁B₁) determinate de două puncte din corp înainte şi după deformare.

Se numesc deformaţii variaţiile dimensiunilor geometrice în vecinătatea unui punct al corpului studiat, ca urmare a solicitărilor aplicate asupra lui. Şi acestea pot fi:

Þ liniare (alungiri sau scurtări) – modificarea distanţei dintre două puncte ale corpului; exemplu DL = A₁B₁ – AB;

Þ unghiulare (lunecări) – modificarea unghiului dintre două segmente din vecinătatea punctului dat.

Mărimile de tip liniar se măsoară în unităţi de lungime, cele unghiulare – în radiani sau, mai rar, în grade.

Pentru a se înlesni compararea deformaţiilor a două corpuri, se apelează la mărimi relative (adimensionale):

Þ deformaţia specifică (e) – raportul dintre deformaţia liniară absolută şi lungimea iniţială

(1.20)

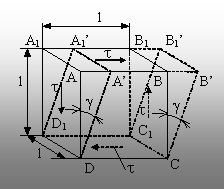
Þ lunecarea specifică (g) – unghiul care marchează variaţia, după deformare, a unghiului iniţial drept dintre două plane din corpul studiat (fig. 1.15); se consideră pozitivă în cazul în care unghiul drept se micşorează.

Fig. 1.15

Deformaţiile specifice liniare (e) şi lunecările specifice (g) reprezintă mărimi fundamentale în studiul rezistenţei materialelor, cu ajutorul cărora se evaluează tipul şi nivelul deformaţiilor unei structuri elastice, sub acţiunea unei anumite solicitări.

Totalitatea valorilor deforma-ţiilor specifice din jurul unui punct dintr-un corp solicitat într-un mod oarecare formează starea de deformaţii din acel punct.

Dacă s-ar măsura, printr-o metodă oarecare, aceste deformaţii specifice, s-ar putea constata că valorile lor se obţin diferite, în funcţie de planul sau direcţia în care se face măsurarea. Din acest motiv, ele se exprimă de obicei prin componentele lor pe axele de coordonate (x), (y) şi (z) ale unui sistem orto-normat oarecare, având originea în punctul considerat, respectiv în planele determinate de aceste axe.

Aceste componente se notează (e_x), (e_y) şi (e_z) – pentru deformaţiile specifice liniare, respectiv (g_xy), (g_yz) şi (g_zx) – pentru lunecările specifice. Pe cunoaşterea lor se bazează studiul amănunţit şi riguros al stărilor de tensiuni şi deformaţii din diverse tipuri de corpuri, în cazul solicitărilor din domeniul elastic al deformabilităţii materialelor, ceea ce formează obiectul unei discipline separate, numită Teoria elasticităţii.