Calculul forţei rezultante

Se începe prin a se pune în evidenţă, ca în figură, forţa elementară (dF) a distribuţiei, reprezentată de suma forţelor (q) care acţionează pe distanţa infinit mică (dx). Valoarea forţei elementare va fi dF = q(x) dx.

Deoarece forţa rezultantă este suma tuturor componentelor q(x) de pe distanţa (b-a) rezultă, la modul general, următoarea relaţie de calcul:

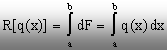(1.3)

Dacă funcţia de distribuţie este cunoscută şi primitiva ei este uşor de calculat, atunci rezultanta se poate stabili imediat, cu relaţia de mai sus. Pe de altă parte însă, cunoscându-se interpretarea geometrică a acestei relaţii, se poate formula următoarea regulă de calcul:

Rezultanta unei forţe distribuite este numeric egală cu aria suprafeţei care reprezintă încărcarea distribuită respectivă.

Prin urmare, pentru încărcările care reprezintă figuri geometrice elementare, se poate evita calculul integralei din relaţia (1.3), înlocuindu-l prin simpla determinare a ariei geometrice a încărcării.

Punctul de aplicaţie a rezultantei va fi centrul de greutate G al suprafeţei care reprezintă încărcarea. Trebuie observat că, în calculele obişnuite, este importantă doar coordonata (x_G), de pe axa barei.

În altă ordine de idei, este important să se precizeze că multe dintre calculele implicate de rezolvarea problemelor de rezistenţa materialelor se preferă a fi efectuate sub formă literală, înlocuirea simbolurilor cu datele numerice urmând a se face doar în relaţiile finale de calcul. Acest mod de lucru permite să se păstreze un grad mare de generalitate în rezolvarea problemelor, precum şi să se menţină legătura, pe parcursul rezolvării, cu fenomenele fizice la care se referă aplicaţia considerată.

De exemplu, intensitatea forţelor distribuite se exprimă prin numere înmulţite cu simbolul (q) – cu unitatea de măsură [N/m], iar distanţele prin numere înmulţite, de obicei, cu (a) sau (l), măsurate în [m]. Prin urmare, rezultanta unei forţe distribuite se va exprima în funcţie de simbolul (q∙a), având ca unitate de măsură [N]. În plus, rezultă că o mărime notată prin factorul (qa) înmulţit cu un număr (întreg sau fracţionar) va reprezenta, în principiu, o forţă concentrată.