Calculul momentului rezultant

Momentul rezultant al unei forţe distribuite, în raport cu un punct arbitrar P, se poate calcula cu relaţia generală de forma:

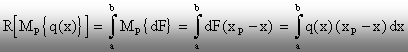(1.4)

Cunoscând, din mecanica teoretică, teorema care precizează că rezultanta momentelor elementare este egală cu momentul, faţă de punctul P, al rezultantei forţelor q(x), rezultă că:

(1.5)

Se observă că această relaţie simplifică mult calculele, astfel că va fi preferată relaţiei (1.4) în toate cazurile în care coordonata (x_G) este uşor de stabilit pentru încărcarea distribuită concretă.

Unitatea simbolică de măsură a momentelor rezultante va fi, în calculele literale, de forma (q∙a²), măsurată în [Nm]. Rezultă că o mărime identificată prin factorul (qa²) înmulţit cu un număr (întreg sau fracţionar) va reprezenta, în principiu, un moment concentrat.

Atenţie: Rezultantele momentelor forţelor distribuite reprezintă momente concentrate imaginare, conform regulilor generale formulate mai sus! Ca urmare, aceste momente vor fi incluse în sumele de momente faţă de axele (z) din diferite puncte ale planului în care acţionează solicitarea, alături de momentele încovoietoare concentrate şi de momentele forţelor concentrate incluse în plan.

Aplicarea practică a noţiunilor prezentate în acest paragraf se va face în cadrul exemplelor privind calculul reacţiunilor.