Ecuaţii de echilibru

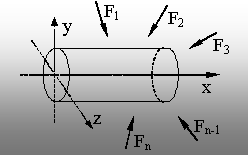
Faptul că un corp solid se află în echilibru (fig. 1.4) sub acţiunea sarcinilor exterioare se poate exprima, din punct de vedere matematic, prin condiţiile de egalitate cu zero a rezultantelor forţelor şi momentelor care îl încarcă.

Fig. 1.4. Studiul stării de echilibru

pentru un corp solid.

În privinţa forţelor, aceasta înseamnă că suma proiecţiilor forţelor, pe fiecare dintre axele de coordonate ale sistemului tri-ortogonal arbitrar (Oxyz), trebuie să fie egală cu zero:

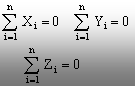(1.6)

Vor fi, prin urmare, trei astfel de ecuaţii, în cazul general, “spaţial”, respectiv două – pentru solicitările care produc efecte într-un singur plan.

Pe de altă parte, este necesar ca suma momentelor produse de toate încărcările aplicate piesei, în raport cu fiecare dintre axele de coordonate duse printr-un punct arbitrar O, să fie zero:

(1.7)

În acest fel se scriu încă trei ecuaţii – într-o problemă “spaţială”, respectiv doar una (în raport cu axa perpendiculară pe planul forţelor, singura axă faţă de care forţele respective pot să producă momente) – în cazul plan.

Rezultă că starea de echilibru a unui corp se exprimă prin şase ecuaţii, în problemele în spaţiu, respectiv prin trei – la solicitările într-un singur plan. Acestea se numesc ecuaţii de echilibru şi sunt folosite la calculul reacţiunilor, adică al forţelor şi momentelor aplicate de reazeme asupra corpului care se propune a fi studiat.

Calculul reacţiunilor este, de obicei, prima etapă în rezolvarea unei probleme de rezistenţa materialelor, întrucât numai după găsirea lor se poate considera cunoscută în întregime încărcarea exterioară a corpului respectiv.

Problemele din rezistenţa materialelor pentru care numărul N al reacţiunilor de determinat este egal cu numărul E de ecuaţii de echilibru care pot fi scrise, deci N = E, se numesc probleme static determinate.

Acele probleme în care numărul N este mai mare decât E se numesc static nedeterminate, iar numărul n = N-E este gradul nedeterminării unei asemenea probleme.

După cum rezultă din definiţia momentului unei forţe în raport cu o axă, în cazul unei probleme plane ecuaţia de echilibru pentru momente se va calcula, de fapt, în raport cu un punct oarecare (P) din planul forţelor de solicitare. Astfel, dacă acest plan include axele (x) şi (y) ale sistemului, atunci se poate scrie că

(1.8)