Aplicaţii: Calculul reacţiunilor în probleme static determinate

Fig. 1.5.

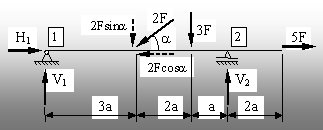
1.1. Bara din fig. 1.5 este articulată în capătul din stânga, (punctul 1) şi simplu rezemată în punctul 2. Cele trei reacţiuni, toate de tip forţă, s-au notat H₁, V₁ şi V₂.

Solicitarea exterioară include o forţă verticală (3F), una orizontală (5F) şi una oblică (2F), înclinată la unghiul (a) faţă de axa barei.

Aşa cum s-a explicat mai sus, se preferă rezolvarea literală, deci toate calculele vor include forţele exprimate în funcţie de parametrul (arbitrar, dar fixat) notat cu (F).

Rezolvare

Se alege punctul 1 ca reper pentru scrierea ecuaţiei de echilibru pentru momente, astfel încât cele trei ecuaţii ale problemei se vor scrie astfel:

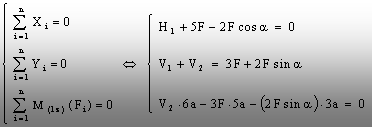
Din aceste ecuaţii se pot deduce valorile (literale) ale reacţiunilor H₁ şi V₂, precum şi o relaţie între cele două reacţiuni verticale:

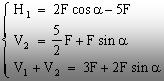(1.9)

Au fost utilizate toate cele trei ecuaţii de echilibru care pot fi scrise în acest caz de solicitare. Totuşi, echilibrul momentelor poate fi exprimat în raport cu oricare punct din planul longitudinal al barei (coincident cu planul desenului). De aici rezultă că reacţiunea V₁ ar putea fi calculată separat, din ecuaţia de momente scrisă în raport cu un punct din plan diferit de punctul 1, ales iniţial. De obicei se preferă cel de-al doilea reazem al barei, pentru ca reacţiunea deja calculată să nu apară în noua ecuaţie.

Acest lucru nu înseamnă că se pot scrie mai multe ecuaţii de momente, independente între ele, adică ecuaţiile de echilibru semnificative rămân în număr de trei. Este vorba doar despre scrierea uneia dintre ecuaţii sub două forme. Această metodă are avantajul că ecuaţia rămasă neutilizată (SY_i = 0) va deveni relaţie de verificare a valorilor calculate ale reacţiunilor, contribuind la .menţinerea controlului asupra corectitudinii rezolvării.

Pentru aplicaţia propusă, ecuaţia de momente faţă de axa (z) din punctul 2 este: (1.10)

Cea de-a doua reacţiune verticală se obţine: V₁ = F/2 + F sina (1.11)

Se observă că suma celor două reacţiuni V este (3F + 2F sina), adică valorile reacţiunilor sunt corecte, deoarece transformă cea de-a treia ecuaţie din sistemul (1.9) într-o identitate.

Reacţiunile care acţionează pe bara din figura (1.5) sunt deci următoarele:

H₁ = F (–5 + 2 cosa) ; V₁ = F (1/2 + sina) ; V₂ = F (5/2 + sina)

Fig. 1.6.

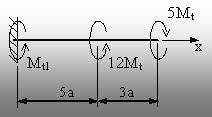
1.2. Bara din figura 1.6 este încărcată numai cu momente de răsucire concen-trate, adică vectori de tip moment care au direcţia axei barei. Rezultă că, dintre cele şase reacţiuni posibile în reazemul încastrat, va fi semnificativă doar cea de tip moment de răsucire (M_t1). Oricare alta nu are vreo solicitare oponentă pe bara considerată, deci va fi nulă.

¨ Momentele de răsucire produc rotiri ale secţiunilor în care acţionează, în plane perpendiculare pe axa barei, astfel încât ele se reprezintă, convenţional, prin arce de cerc (cu săgeţi care indică sensul rotirii) “turtite”, spre a fi deosebite de momentele care produc rotiri în alte plane decât cele transversale.

¨ Folosind în continuare calculele literale, toate momentele se exprimă în funcţie de parametrul (arbitrar, dar fixat) notat cu (M_t).

Rezolvare

Pentru solicitările de acest fel se poate scrie o singură ecuaţie de echilibru:

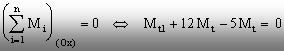(1.12)

Pentru problemele static determinate (cu o singură necunoscută), această ecuaţie conduce imediat la finalizarea calculelor. Aici: M_t1 = –7 M_t

¨ După cum a reieşit şi din rezolvarea problemei 1.1, în scrierea ecuaţiilor de echilibru nu sunt necesare convenţii de semne, deoarece este vorba despre sume de termeni egale cu zero. Aceste ecuaţii pot fi oricând înmulţite cu numărul (–1), schimbând astfel semnele tuturor termenilor. În principiu, primul termen al unei asemenea ecuaţii se consideră pozitiv, iar ceilalţi termeni vor avea semnele rezultate din comparaţia cu primul.

¨ Sensurile reacţiunilor se aleg arbitrar, la începutul rezolvării, fără vreo implicaţie specială asupra calculelor. Cele care acţionează, în realitate, în sens contrar celui de pe desenul barei, vor rezulta din calcule cu semnul (–) (ca în problema 1.2 de mai sus), ceea ce nu prezintă nici un inconvenient pentru etapele ulterioare ale rezolvării problemelor de rezistenţa materialelor.

Fig. 1.7.

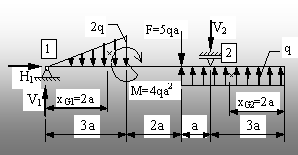
1.3. Bara din figura 1.7 este sprijinită pe un reazem simplu (în punctul 2) şi pe o articulaţie (în 1) şi încărcată cu o forţă concentrată verticală (F = 5qa), un moment concen-trat (M = 4qa²), de sens orar (în planul desenului), o forţă distribuită uniform, de intensitate (q), pe lungimea (4a), precum şi o forţă distribuită liniar, pe lungimea (3a), având intensităţile extreme 0 şi (2q).

¨ Pe desen s-au reprezentat şi abscisele centrelor de greutate ale încărcărilor distribuite, care vor fi utilizate în calculele de mai jos.

¨ Momentul concentrat (M) produce rotirea barei, în jurul direcţiei momentului, în planul desenului (adică solicitare de încovoiere în jurul axei (z) din punctul în care se aplică M), astfel că se reprezintă printr-un arc de cerc (cu săgeată de sens) “real” (nedeformat).

¨ Aşa cum s-a explicat mai sus, prezenţa forţelor distribuite implică necesitatea exprimării solicitărilor în funcţie de parametrii (q) şi (a). Este de precizat faptul că acest fel de exprimare este posibil în oricare caz concret de solicitare, făcându-se raportul între mărimile concrete ale forţelor şi momentelor concentrate de pe bară şi valorile mărimilor [qa], respectiv [qa²], exprimate numeric, în funcţie de datele problemei.

Exemplu: Să presupunem că, pentru problema considerată, se dau valorile a=0,2m şi q=20kN/m, iar sarcinile concentrate sunt M=3,2kNm şi F=20kN. Produsele de mai sus vor avea valorile qa=4kN şi qa²=0,8kNm. Rezultă:

M = 4qa² şi F = 5qa.

Este evident că aceste rapoarte pot fi calculate în orice problemă de acest fel, iar eventualele lor valori fracţionare nu influenţează calculele ulterioare.

Rezolvare

Pe bară apar trei reacţiuni, toate de tip forţă, notate cu H₁, V₁ şi V₂. Cele trei ecuaţii de echilibru care pot fi scrise fac ca problema să fie static determinată.

Pe de altă parte, echilibrul proiecţiilor de forţe pe direcţie orizontală se scrie, simplu, H₁=0, deci în problemă există doar două necunoscute, dar şi numai două ecuaţii de echilibru semnificative.

Echilibrul proiecţiilor verticale ale forţelor conduce (ţinând seama că rezultanta unei forţe distribuite este egală numeric cu aria geometrică a desenului încărcării) la următoarea ecuaţie:

(1.13)

După reducerea termenilor asemenea, se obţine: V₁–V₂ = 4qa (1.14)

La fel ca la problema 1.1, se preferă calculul independent al celor două reacţiuni, din ecuaţiile de echilibru al momentelor faţă de cele două reazeme (la care se ţine seama de poziţiile centrelor de greutate ale încărcărilor distribuite, deci ale rezultantelor de tip forţă ale acestora):

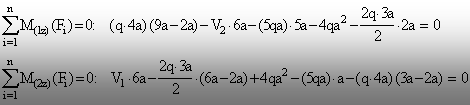
Ca principiu, scrierea acestor ecuaţii se începe cu solicitările dintr-un capăt al barei, studiindu-se apoi efectul fiecărei încărcări, ca moment în raport cu punctul considerat, pe măsura parcurgerii imaginare a barei către celălalt capăt al ei.

Rezultat După reducerea termenilor asemenea în ecuaţiile de mai sus se ajunge la următoarele valori ale reacţiunilor verticale:

V₁ = (17/6) qa V₂ = (–7/6) qa

Verificare V₁–V₂ = (24/6) qa = 4qa adevărat, conform (1.14)

deci rezultatele obţinute sunt corecte.

Concluzii (pentru barele drepte, static determinate, cu încărcări care produc efecte în planul desenului)

· Dacă nu există pe bară forţe exterioare de direcţie diferită de verticală, atunci reacţiunea orizontală din articulaţie este nulă.

· Forţele distribuite de o parte şi de alta faţă de un reazem pot fi luate în calcul ca şi cum ar fi divizate în două forţe distincte (prin ariile şi centrele de greutate ale figurilor geometrice respective), dar cel mai simplu este să se considere efectul lor global.

Fig. 1.8

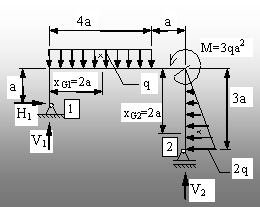
1.4. Bara din figura 1.8 are axa cotită, fiind formată din două segmente verticale, de lungimi (a) şi (3a) şi unul orizontal de lungime (4a). Capătul 1 este articulat, iar 2 – simplu rezemat, pe verticală.

Sarcinile sunt:

· un moment concentrat (M=3qa²), de sens antiorar;

· o forţă distribuită uniform, de intensitate (q), pe lungimea (4a);

· o forţă distribuită liniar, pe lungimea (3a), cu valorile extreme 0 şi (2q).

Este evidentă similitudinea acestui caz de solicitare, în privinţa schematizării barei şi încărcărilor ei, cu situaţia din problema precedentă. Calculele vor fi diferite numai pentru că axa acestei bare nu are aceeaşi direcţie pe toată lungimea ei.

Rezolvare

Cele trei reacţiuni, de tip forţă, s-au notat cu H, V₁ şi V₂.

Echilibrul proiecţiilor de forţe pe cele două direcţii ale planului se scrie:

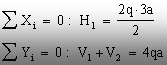(1.15)

Cele două reacţiuni verticale se calculează independent, scriind echilibrul momentelor faţă de cele două reazeme, astfel:

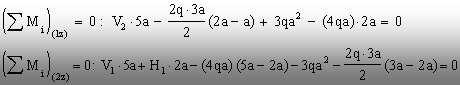
Rezultat După reducerea termenilor asemenea (înlocuind pe H₁ cu 3qa), se ajunge la următoarele valori ale reacţiunilor:

V₁ = (12/5) qa V₂ = (8/5) qa H₁ = 3qa

Verificare V₁ + V₂ = (20/5) qa = 4qa

adică rezolvarea a fost corectă, confirmând a doua ecuaţie (1.15).