Ipoteze de bază

Pentru a se realiza modelarea situaţiilor reale de solicitare, se iau în considerare câteva ipoteze simplificatoare asupra structurii şi comportării materialelor, după cum se va arăta în continuare.

à Ipoteza mediului continuu – materialul reprezintă un mediu lipsit de discontinuităţi, omogen, ocupând întregul spaţiu reprezentat de volumul său; această ipoteză este mai apropiată de realitate în cazul materialelor amorfe, fiind doar aproximativă pentru cele cristaline.

à Ipoteza izotropiei – încercări efectuate pe oricare direcţie din structura materialului conduc la aceleaşi valori pentru constantele elastice (E, G, n), proprietăţile mecanice, electrice ş.a.m.d.

à Ipoteza elasticităţii perfecte – apropiată de realitate, deoarece în mod obişnuit materialele sunt solicitate sub limita lor de elasticitate, deci deformaţiile pe care le suportă sunt reversibile.

à Ipoteza deformaţiilor mici (faţă de dimensiunile corpului) – din care rezultă, de exemplu, că ecuaţiile de echilibru pot fi scrise la fel, pentru corpul deformat şi nedeformat, deoarece direcţiile forţelor şi distanţele dintre ele nu se modifică în urma deformării. În plus, în expresiile matematice care includ şi valori ale deformaţiilor, termenii care conţin puteri ale acestor valori pot fi neglijaţi (ca “infiniţi mici de ordin superior”), ceea ce constituie aşa-numita “teorie de ordinul întâi”. În teoria de ordinul al doilea utilizată, de pildă, la calculele de stabilitate, se iau în considerare şi deformaţiile în scrierea ecuaţiilor de echilibru.

à Ipoteza relaţiei liniare între eforturi şi deformaţii – deschide posibilitatea aplicării principiului “suprapunerii efectelor” (al independenţei efectelor) încărcărilor. Acest principiu permite simplificarea calculelor şi poate fi aplicat în toate cazurile în care există o relaţie liniară între două mărimi fizice (pentru materialele liniar-elastice, asemenea relaţii există între forţe şi deplasări, între momente şi rotiri, dar şi între tensiuni şi deformaţiile specifice). Ipoteza se foloseşte şi pentru extinderea aplicabilităţii relaţiilor de calcul deduse pentru materialele elastice,care deci se folosesc şi pentru materialele care nu respectă legea lui Hooke.

à Principiul lui Saint-Venant – la distanţă suficientă de locul de aplicare, efectele a două forţe având aceeaşi intensitate sunt aceleaşi, chiar dacă ele sunt aplicate în mod diferit (concentrat sau distribuit).

Fig. 4.1. Verificarea ipotezei lui Bernoulli în cazul barelor supuse

la încovoiere.

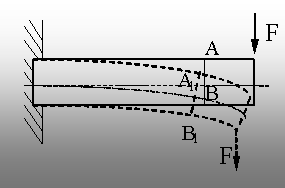
à Ipoteza lui Bernoulli – o secţiune plană şi normală la axa unei bare înainte de deformarea ei printr-o solicitare oarecare rămâne plană şi perpendiculară pe axă şi după deformare. Ipoteza se respectă în mod riguros la tracţiune, dar şi la răsucirea barelor de secţiune circulară. Ea aduce simplificări în calculele legate de distribuţia tensiunilor pe secţiunile barelor, mai ales la încovoiere (fig. 4.1), faţă de calculele din teoria riguroasă a elasticităţii.

Ipoteza stării naturale – pentru un corp, o rezemare şi un sistem de sarcini date, starea de tensiuni şi deformaţii este unică (adică se neglijează eventualele tensiuni remanente din materialul piesei).