Energia potenţială de deformare

Pe măsură ce se produc deformări ale unei bare, sub acţiunea unei anumite solicitări, consumul de lucru mecanic duce la acumularea în bară a unei energii potenţiale de deformare. Această cantitate de energie este eliberată atunci când se produce descărcarea (eliberarea) corpului respectiv, ceea ce determină reversibilitatea deformaţiilor, dacă este respectată condiţia ca solicitarea să nu depăşească limita de elasticitate a materialului considerat.

Dacă în urma încărcării şi descărcării complete a unui corp solid, în cadrul unui proces reversibil de deformare, variaţia energiei potenţiale este nulă, atunci sistemul format din acel corp şi încărcările aplicate asupra lui se numeşte conservativ (nu are “pierderi” de energie).

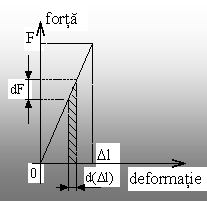
Se ia în considerare, ca exemplu, o bară cilindrică, dreaptă, solicitată la tracţiune prin forţa axială F, care conduce la alungirea barei cu cantitatea (DL). În aceste condiţii, lucrul mecanic efectuat de forţa exterioară, atunci când se deplasează pe o distanţă elementară dd, se va numi lucru mecanic elementar şi se va calcula cu relaţia: dL = F(d)×dd.

Prin urmare, lucrul mecanic total se va obţine prin integrare:

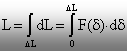(4.4)

Dacă se analizează diagrama din figura 4.2, se observă că integrala din relaţia (4.4) are ca interpretare geometrică aria suprafeţei cuprinse între graficul dependenţei F - (d) şi axa absciselor.

Fig. 4.2. Lucrul mecanic elementar

Deoarece se discută despre domeniul elastic al deformabilităţii materialului barei, în care dependenţa dintre cele două mărimi este liniară, rezultă că lucrul mecanic de deformare va fi dat de aria triunghiului de sub grafic.

Pe această bază rezultă că lucrul mecanic necesar pentru deformarea barei în modul descris a va fi:

(4.5)

O discuţie cu totul similară se poate face pentru o solicitare produsă de un moment concentrat M, căruia îi corespunde deformaţie unghiulară (Dj) a barei, în secţiunea în care acţionează momentul M. Prin urmare, în acest caz lucrul mecanic de deformare va fi:

(4.6)

În cazul cel mai general, în care atât sarcinile exterioare, cât şi deplasările şi rotirile sunt date (ca în expresia de mai jos) prin proiecţiile lor pe axele unui sistem tri-axial de coordonate, în conformitate cu ipoteza proporţionalităţii între sarcini şi deformaţii (deci cu “principiul suprapunerii efectelor”), efectele solicitărilor nu depind de ordinea aplicării lor, iar expresia globală a lucrului mecanic exterior poate fi scrisă astfel:

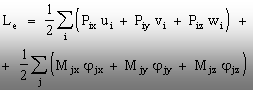(4.7)

Pe de altă parte, pentru un corp elastic aflat în repaus lucrul mecanic al sarcinilor exterioare care acţionează asupra lui este considerat egal ca mărime cu energia potenţială de deformare acumulată în corp:

(4.8)

Expresiile (4.7) şi (4.8) sunt cunoscute, în studiul rezistenţei materialelor şi al teoriei elasticităţii, drept teoremele lui Clapeyron.