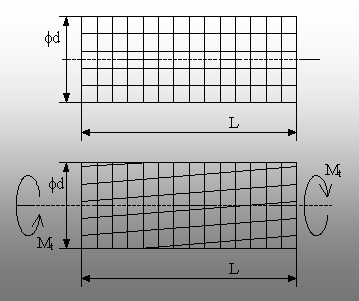
Tensiuni şi deformaţii specifice

Se consideră o bară cilindrică, având lungimea L şi diametrul d, pe a cărei suprafaţă se trasează o reţea de linii reprezentând generatoare şi circum-ferinţe. Ochiurile reţelei astfel obţinute au formă de pătrate curbilinii.

Dacă se aplică, la capetele barei, doi vectori moment de mărimi egale şi de sensuri contrare (fig. 6.1), atunci bara este solicitată la răsucire, iar prin analiza efectelor acestei solicitări se observă următoarele:

· Dimensiunile barei nu se schimbă, pe nici o direcţie, după aplicarea solicitării.

· Secţiunile care erau iniţial plane şi perpendiculare pe axa barei îşi păstrează aceste caracteristici după producerea solicitării, chiar dacă se rotesc în jurul axei longitudinale. Rezultă că, în cazul răsucirii barelor de secţiune circulară, se respectă în mod riguros ipoteza lui Bernoulli.

Fig. 6.1. Deformarea prin răsucire a barelor cilindrice.

· Se produc doar rotiri reciproce ale secţiunilor transversale, astfel că liniile generatoare devin elicoidale, iar pătratele iniţiale ale reţelei de linii se transformă în paralelograme curbilinii. Rezultă că în bară se produc numai deformaţii specifice de lunecare, adică lunecări specifice (g), cărora le corespund tensiuni tangenţiale (t).