Deducerea relaţiilor pentru calculele de rezistenţă

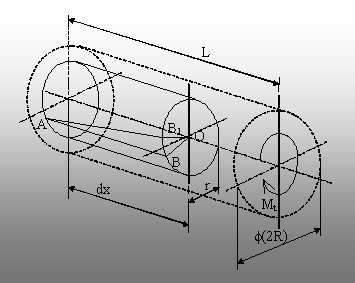
Se consideră o bară cilindrică, de diametru (2R) şi lungime L (fig. 6.2), având capătul dinspre stânga fixat, iar pe celălalt liber – în dreptul lui acţionând un moment de răsucire M_t.

Se izolează din bară un element de volum, de formă cilindrică, de lungime (dx) şi rază r, iar pe suprafaţa lui exterioară se trasează o generatoare AB. După aplicarea momentului M_t, în urma rotirii secţiunii de capăt a elementului de volum considerat, generatoarea AB devine elice, iar punctul B se deplasează în B₁.

Fig. 6.2.

Întrucât cele două secţiuni care mărginesc volumul elementar se află la distanţa (dx), se defineşte unghiul (dj) dintre razele OB şi OB₁ drept rotirea elementară a secţiunii respective, iar unghiul dintre poziţia iniţială AB şi cea finală AB₁ ale generatoarei considerate reprezintă mărimea lunecării specifice (g) care se produce în materialul barei. Prin urmare, se fac notaţiile:

Se observă că, în baza trigonometriei elementare, se poate scrie: B₁B=r dj. Pe de altă parte, din triunghiul dreptunghic B₁AB (cu laturile curbilinii suficient de mici pentru a fi asimilate unor segmente de dreaptă), cum unghiul g este foarte mic, rezultă:

B₁B = AB tgg = g dx

Egalând cele două relaţii care dau mărimea lui B₁B şi ţinând seama că se defineşte rotirea specifică, pentru elementul de volum considerat, sub forma q=dj/dx, se obţine o relaţie de legătură între lunecarea specifică şi rotirea specifică, astfel:

Se introduce această exprimare a lui g în expresia (3.7) – legea lui Hooke pentru solicitarea de răsucire – ajungându-se la o relaţie pentru calculul tensiunilor tangenţiale din secţiunile transversale ale barei:

(6.2)

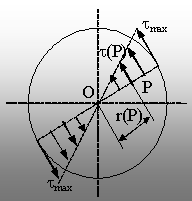
Pentru o stare dată de solicitare, rotirea specifică q este constantă, cel puţin pentru o secţiune a unei bare cilindrice, dacă nu pentru porţiuni (regiuni) întregi de pe lungimea ei. Prin urmare, dacă se consideră o secţiune transversală oarecare a barei din figura 6.2, tensiunea tangenţială dintr-un punct arbitrar P (fig. 6.3) depinde numai de distanţa dintre punctul P şi centrul O al secţiunii, adică de raza acelui punct, r(P).

Fig. 6.3.

Cum relaţia (6.2) arată o directă propor-ţionalitate între cele două mărimi, rezultă că tensiunile t au o evoluţie liniară pe orice rază a secţiunii, având valoarea 0 în centru şi valoarea maximă (t_max) pe circumferinţă, unde r=R. Figura 6.3 prezintă variaţia tensiunilor pe diametrul care trece prin punctul arbitrar P.

Aşadar, punctele de pe o secţiune transversală aflate la aceeaşi distanţă faţă de centru (deci pe cercul de rază r) sunt caracte-rizate de o aceeaşi valoare a tensiunii tangenţiale de răsucire, iar tensiunea maximă se înregistrează pe conturul exterior al secţiunii, având mărimea:

(6.3)

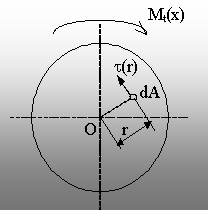
Fig. 6.4.

Dacă se pune în evidenţă un element de arie dA, situat la raza r, tensiunea care îi cores-punde se notează t(r), iar efectul global al tuturor tensiunilor de acest fel trebuie să echilibreze momentul M_t(x), care reprezintă efortul din secţiunea considerată (fig. 6.4).

Cu alte cuvinte, ecuaţia care exprimă echilibrul momentelor faţă de axa longitu-dinală a barei se scrie sub forma:

Aceasta reprezintă ecuaţia de echivalenţă dintre tensiuni şi efortul secţional, de tipul (1.18), pentru secţiunea analizată.

Introducând în această ecuaţie expresia (6.2) a tensiunilor, se ajunge la relaţia:

Ultima integrală de mai sus este, conform definiţiei (2.6), exprimarea matematică a modulului de inerţie polar I_p(x) al secţiunii. Prin urmare, se poate scrie că:

(6.4)

şi înlocuind acest rezultat în relaţia (6.2) se obţine formula finală pentru calculul tensiunilor tangenţiale efective dintr-un punct aflat în secţiunea (x), la distanţa r de axa barei:

(6.5)

După cum s-a arătat, valoarea maximă a tensiunilor dintr-o secţiune se obţine în punctele cele mai depărtate de axa barei, adică:

Dacă, în această relaţie, se trece mărimea (r_max) la numitorul numitorului, atunci se obţine relaţia de definiţie (2.16) a modulului de rezistenţă polar W_p. Pe de altă parte, pentru o bară sau un tronson de bară de secţiune constantă, rezultă că solicitarea cea mai periculoasă va avea loc în secţiunea în care momentul de răsucire este maxim. Din aceste două considerente se deduce că relaţia pentru calculele de rezistenţă, în cazul barelor de secţiune circulară solicitate la răsucire, se scrie astfel:

(6.6)

Problemele de acest fel necesită parcurgerea următoarelor etape:

· Trasarea diagramei momentelor de răsucire M_t(x) – pentru stabilirea secţiunilor transversale în care solicitarea este maximă.

· Trasarea diagramei t_max(x) – aflarea valorii maxime a tensiunilor efective din piesă.

· Particularizarea inecuaţiei (6.6) pentru secţiunea periculoasă.

· Efectuarea calculelor cerute de problemă.