Exemplu de calcul
|
Fig. 6.5. |
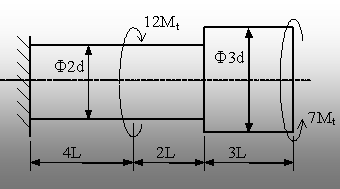
6.1. Se consideră o bară cilindrică în
consolă, formată din două tronsoane de diametre şi lungimi
diferite şi solicitată prin două momente concentrate de
răsucire (fig. 6.5).
Se cere dimensionarea barei (adică
să se determine valoarea necesară a para-metrului d), dacă Mt=20kNm,
iar ta=120MPa.
Se observă
că se menţine exprimarea parametrică a datelor problemei, deci
şi rezolvarea ei se va face literal, cu respectarea principiilor de calcul
explicate anterior.
Pe de altă parte, este important să fie remarcată,
în toate paragrafele acestui capitol, similitudinea dintre raţionamentele
făcute în legătură cu solicitările axiale şi cele de
la răsucire. Ea se datorează faptului că ambele categorii de
solicitări sunt produse prin vectori (forţe, respectiv momente) care
au direcţia axei longitudinale a barei.
Rezolvare
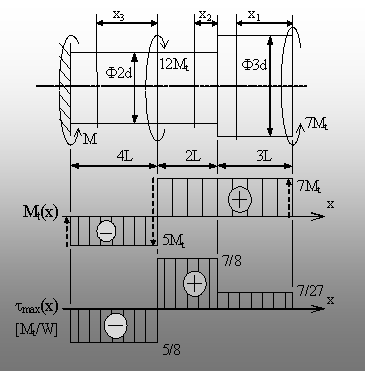
Punctele de aplicare a momentelor
delimitează pe bară două regiuni, iar saltul de secţiune de
la interfaţa tronsoanelor conduce la apariţia celei de-a treia (fig.
6.6).
|
Fig. 6.6. |
Se alege varianta de
măsurare a variabilei x de la capătul din dreapta al fiecărei
regiuni, aşa cum se arată în figură.
Bara este solicitată numai
prin momente de direcţie axială, deci în încastrare există un
singur tip de reacţiune, momentul M, iar singura ecuaţie de echilibru
semnificativă se scrie:
M – 12Mt
+ 7Mt = 0
de unde rezultă că M =
5Mt.
Acest rezultat arată că
reacţiunea are, în mod real, sensul indicat pe desen.
A. Trasarea diagramelor
Se trece la stabilirea
parametrilor solicitării, pe regiuni. Se reaminteşte că nu
există o diferenţă de efecte între cele două sensuri
posibile ale momentelor de răsucire, astfel încât semnele eforturilor de acest tip sunt cu totul arbitrare. Singura
condiţie care trebuie avută în vedere este ca rezultatul calculelor
să fie acelaşi, indiferent de poziţia faţă de
secţiune a părţii de bară de pe care se sumează
încărcările. Din acest motiv, convenţia
de semne pentru partea din dreapta trebuie să fie inversă celei din
partea stângă!
Pentru x1Î(0; 3L) efortul axial este Mt(x1) = 7Mt
= ct.
Acest calcul s-a făcut
pentru încărcările din partea dreaptă faţă de
secţiune, considerând pozitive momentele de sensul celui din capătul
barei, adică acelea care, privind dinspre dreapta, rotesc bara în sens
orar.
Dacă se
verifică şi suma momentelor din partea stângă, inversând
convenţia de semne, se obţine:
Mt(x1)
= –5Mt + 12Mt = 7Mt
ceea ce confirmă cerinţa de a se respecta regula
menţionată mai sus.
Folosind simplificarea scrierii,
prin notaţia ![]()
, se calculează modulul de rezistenţă polar al
secţiunilor transversale de pe primul tronson al barei, astfel:
![]()
Tensiunile maxime din
această primă regiune se determină cu o relaţie de forma
(6.6), adică:
![]()
Este uşor
de remarcat că toate mărimile de calcul se exprimă în
funcţie de parametri literali, ceea ce va înlesni compararea valorilor lor
de pe diferite regiuni ale barei.
Pentru cea de-a doua regiune, cu x2Î(0; 2L),
se obţin următoarele rezultate:
Mt(x2)
= 7Mt = ct. ![]()
![]()
În fine, pentru x3Î(0;
4L), valorile sunt:
Mt(x3)
= 7Mt – 12Mt = –5Mt = ct. Wp(x3) = 8W ![]()
Folosind aceste rezultate, se
trasează diagramele din figura 6.6, făcând şi observaţiile
ce urmează:
Pentru diagrama de efort de răsucire Mt(x)
Ř Pe
bară există două zone distincte, ca sens al eforturilor
secţionale.
Ř Graficul
prezintă trei puncte de discontinuitate (salturi – indicate pe desen prin
săgeţi cu linii punctate), care coincid ca punct de apariţie,
mărime şi sens cu momentele concentrate de pe bară.
Ř Saltul
din dreptul reazemului confirmă valoarea reacţiunii M, precum şi
sensul ei, acelaşi cu al momentului 7Mt, din capătul
barei.
Se poate observa că, în
problemele de acest tip, reacţiunea poate fi determinată direct, din
diagrama de efort, fără a se mai scrie ecuaţia de echilibru,
deci făcând rezolvarea mai rapidă.
Pe de altă
parte, trebuie subliniat că simpla cunoaştere a efortului din
secţiunile transversale ale barei nu este suficientă pentru a se
evidenţia solicitarea maximă din piesă. Aceasta va fi
influenţată de modulul de rezistenţă al secţiunii pe
care se distribuie efortul, adică de valorile tensiunilor maxime din
bară.
Diagrama
tensiunilor maxime tmax(x)
Ř Acest
grafic conţine trei zone distincte, care coincid cu regiunile de pe
bară. Punctele de discontinuitate sunt determinate de modificarea valorilor
Mt(x) şi Wp(x), deci salturile nu au o
semnificaţie fizică.
Ř Intensitatea
solicitării este perfect vizibilă pe diagramă. Secţiunea
periculoasă (în care bara se poate distruge, dacă parametrii ei sau
ai încărcărilor sunt aleşi incorect) este oricare dintre
secţiunile transversale de pe regiunea de mijloc a barei, de lungime (2L).
Ř Calculele
de rezistenţă se vor baza pe o relaţie de forma (6.6), astfel:
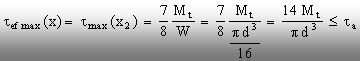 (6.9)
(6.9)
Observaţii
1.
Este interesant de subliniat că în
această relaţie nu apare parametrul L, deci calculele de
rezistenţă nu sunt influenţate de lungimea barei.
2.
Deoarece semnele eforturilor de
răsucire sunt arbitrare, este suficientă scrierea unei singure
relaţii de forma (6.6), pe baza valorii maxime, în modul, a tensiunii efective
din piesă:
B. Dimensionarea barei
Din inecuaţia (6.9)
rezultă, pe baza datelor problemei, că:
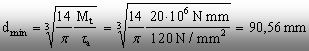
Pe această bază se
adoptă o valoare convenabilă a parametrului d, cum ar fi, de exemplu, dad=100mm.