Exemplu de calcul

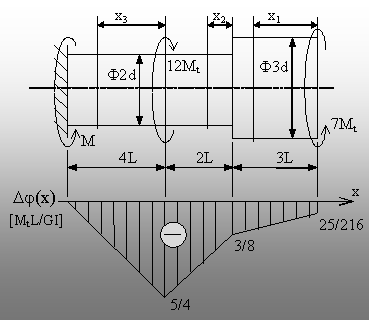
6.2. Pentru bara din figura 6.5, se propune a se trasa diagrama de variaţie, pe axa longitudinală a barei, a rotirilor secţiunilor transversale, Dj(x). Se mai cer următoarele:

a) Să se calculeze valoarea concretă a celei mai mari rotiri a unei secţiuni, dacă se cunosc L=0,1m, G=8×10⁴MPa, M_t=20kN×m şi d=100mm (adoptat anterior).

b) Să se determine valoarea maximă a parametrului M_t pentru care rotirea maximă nu depăşeşte valoarea 0,1 grade.

Rezolvare

Bara fiind solicitată numai la răsucire, rezultă că secţiunile ei se vor deplasa prin rotire, în sens orar sau trigonometric, faţă de poziţia pe care o au în bara lipsită de încărcări.

Dacă se ţine seama de studiul făcut anterior asupra barei rezultă, pe baza consecinţelor 1 şi 3 de mai sus, că:

Þ deformaţia absolută a celor trei tronsoane de bară se calculează cu câte o relaţie de forma (6.12);

Þ funcţia rotirilor Dj(x) are gradul cu o unitate mai mare decât al funcţiei M_t(x), deci va fi o funcţie de gradul întâi (liniară);

Þ întrucât nu interesează atât expresia analitică a acestei funcţii, cât valorile (deci graficul) ei, este suficient să se calculeze aceste valori pentru secţiunile de capăt ale celor trei regiuni de pe bară, iar graficul se va obţine prin unirea, cu segmente de dreaptă, a acestor trei puncte.

Pe de altă parte, este clar că unul dintre punctele graficului este cunoscut de la început, deoarece capătul prins în reazem al barei nu se poate deplasa, deci graficul va începe de la valoarea zero.

Studiul se va continua, pe baza regulii de calcul de mai sus, prin parcurgerea imaginară a barei, din reazem către capătul liber, cu păstrarea notaţiilor din etapa anterioară de rezolvare a problemei.

Mai întâi este necesar să se calculeze momentele polare de inerţie ale secţiunilor transversale de pe cele trei regiuni ale barei. Pentru simplificarea scrierii, se propune să se facă notaţia , rezultând că:

Păstrând convenţia de a exprima toate mărimile în funcţie de anumiţi parametri literali, unghiurile cu care se rotesc (faţă de reazem, sau de poziţia lor în bara nesolicitată) secţiunile de capăt, dinspre dreapta, ale celor trei tronsoane de bară, calculate cu relaţii de forma (6.12), vor fi următoarele:

Fig. 6.7. Trasarea diagramei rotirilor.

Aceste valori se regăsesc pe diagrama rotirilor secţiunilor transversale ale barei (fig. 6.7).

Având în vedere faptul că semnul roti-rilor este determinat de cel al eforturilor secţionale (semn care a fost, la rândul său, ales arbitrar), rezultă că rotirile tuturor sec-ţiunilor se produc în sensul momentului concentrat considerat negativ, adică 12M_t.

Cel mai mare unghi de rotire se produce în secţiunea de la capătul din dreapta al tronsonului de lângă reazem.

Este remarcabil faptul că modul în care se exprimă rotirea unei secţiuni oarecare depinde în mod hotărâtor de secţiunea de pe bară care se alege ca reper. Astfel, calculele de mai sus s-au făcut în raport cu secţiunea prinsă în reazem, care deci nu se poate roti (altfel spus, rezultatele exprimă rotirile faţă de poziţiile secţiunilor în bara lipsită de solicitare).

Dacă însă am alege ca reper, de pildă, secţiunea x₃=0, atunci am obţine rotiri de semn pozitiv ale celorlalte două secţiuni de calcul (aşa cum se observă din semnul pozitiv al fracţiilor care corespund regiunilor din dreapta în expresiile anterioare).

Folosind diagrama rotirilor, se poate trece la efectuarea calculelor numerice precizate în enunţul problemei, aşa cum se arată în continuare.

a) Calculul unghiului maxim de rotire efectivă

Dacă se introduc datele numerice din enunţ în expresia valorii extreme din diagramă, se ajunge la următorul rezultat:

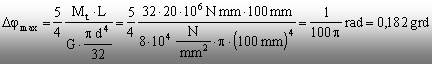
b) Calculul momentului admisibil, dacă se impune o limită a deformaţiei unghiulare

Luând în considerare criteriul de rigiditate se determină, folosind o relaţie de forma (6.15), valoarea maximă permisă a parametrului prin care se exprimă momentele de răsucire. Practic, se egalează expresia de mai sus a unghiului maxim cu rotirea admisibilă Dj_a=0,1grd, de unde rezultă că:

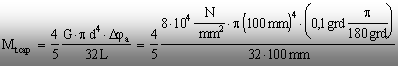
Ultima paranteză de la numărătorul fracţiei mari reprezintă relaţia de transformare, din grade în radiani, a valorii unghiului de rotire maxim admis.

Efectuând calculele se obţine M_{t cap}=10966×10³Nmm deci, pentru ca bara să respecte limita de deformabilitate impusă, valoarea efectivă a parametrului M_t nu trebuie să depăşească 11kNm.