A. Rezolvare pe baza teoremei lui Castigliano

Pentru aplicarea teoremei este necesar ca în secţiunile de calcul să acţioneze momente concentrate de direcţie axială, exprimate independent de celelalte încărcări din sistem.

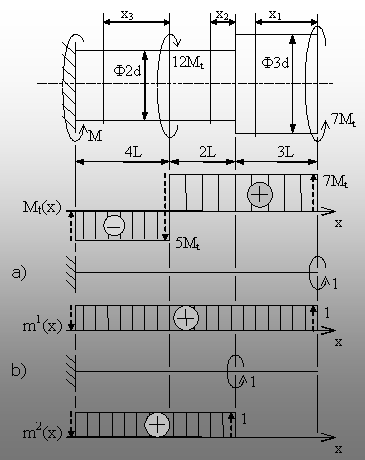
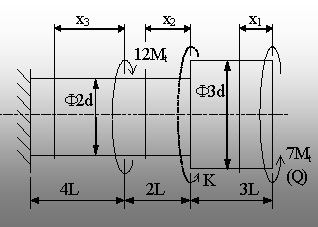
Fig. 6.9.

Din acest motiv se notează prin Q momentul (7M_t) din capătul liber al barei, iar în capătul celălalt al tronsonului din dreapta se introduce un moment fictiv K (de mărime reală zero), alegând să aibă sensul lui Q (fig. 6.9).

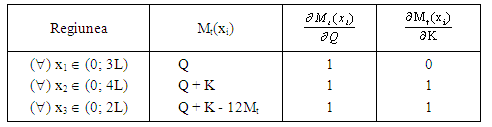
Regiunile de pe bară se iau la fel ca în aplicaţia precedentă, iar eforturile secţionale şi derivatele lor parţiale în funcţie de forţele considerate vor fi următoarele:

Rotirea capătului liber (x₁=0) se va obţine introducând în relaţia (6.19) termenii corespunzători lui (Q) şi dând eforturilor M_t(x_i) valoarea lor reală (cu Q=7M_t şi K=0). Rezultă că:

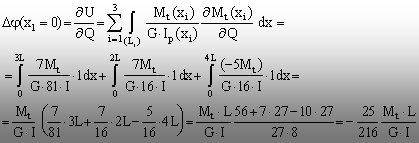(6.23)

Un calcul analog, în raport cu momentul fictiv (K), duce la aflarea rotirii secţiunii de la celălalt capăt (x₂=o) al tronsonului din dreapta, astfel:

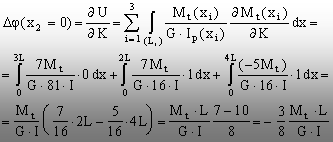(6.24)

2Se observă că valorile obţinute coincid cu cele de la calculele făcute prin metoda geometrică.

Semnul lor negativ arată că secţiunile transversale de calcul se rotesc în sens invers momentelor concentrate care le încarcă, ceea ce s-a observat şi din calcu-lele anterioare