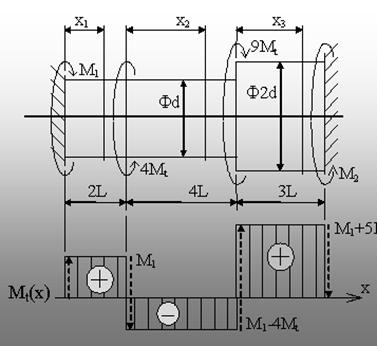
Fig. 6.12.

A1. Aplicarea metodei geometrice

În acest caz se foloseşte condiţia de fixare a capetelor barei, care conduce la o ecuaţie (6.29).

Pentru aceasta este nevoie să se cunoască valorile parametrilor M_t(x) şi I_p(x), pe regiuni, în exprimare literală.

Pentru x₁=(0; 2L)

M_t(x₁)=M₁





Notând
, rezultă că I_p(x₁)=I.

Pentru x₂=(0; 4L) M_t(x₂) = M₁ – 4M_t I_p(x₂)=I

Pentru x₃=(0; 3L) M_t(x₃) = M₁ + 5M_t I_p(x₃)=16 I

Se observă că, în expresiile eforturilor secţionale, s-au considerat pozitive momentele care acţionează în sensul momentelor concentrate M₁ şi 9M_t.

Diagrama de momente poate fi schiţată, în această exprimare dependentă de necunoscuta M₁, aşa cum se arată în figura 6.12. Ecuaţia de tipul (6.29) va avea trei termeni, sub formă de fracţii, astfel:

(6.30)

Înmulţind această ecuaţie cu fracţia (strict pozitivă) , se obţine o ecuaţie cu singura necunoscută M₁ (deoarece toate eforturile secţionale s-au calculat din partea stângă a barei, în raport cu secţiunile considerate):

32M₁ + 64M₁ – 256M_t + 3M₁ + 15M_t = 0

Rezultă că , iar ecuaţia de echilibru duce la

ceea ce înseamnă că nedeterminarea a fost îndepărtată.

Atenţie: De obicei se preferă a se lucra, în etapele următoare ale rezolvării, cu aceste valori numerice, fracţionare, ale reacţiunilor, deoarece transformarea lor în numere zecimale implică, în principiu, rotunjiri, deci apariţia în calcule a unor valori aproximative.