Aplicarea teoremelor lui Castigliano la barele solicitate axial

Aici este aplicabilă numai prima teoremă a lui Castigliano (deoarece în barele solicitate axial nu se produc deformaţii unghiulare). Pe baza acestei teoreme şi folosind ultima egalitate din relaţia precedentă, se poate calcula deplasarea unui punct P de pe axa barei, pe direcţia şi în sensul forţei axiale (F) care se aplică în punctul respectiv, astfel:

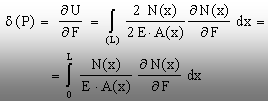(5.36)

Observaţii:

1. S-a calculat derivata în raport cu forţa (F) a expresiei energiei potenţiale de deformare, ca pentru o funcţie compusă, înainte de efectuarea integralei.

2. Dacă este vorba despre un sistem de (n) bare, atunci integrala pe lungimea (L) se va desface în (n) integrale pe lungimile (L_i) ale barelor, iar termenii de sub integrală se vor particulariza pentru fiecare bară a sistemului.

3. Dacă rezultatul calculului este negativ, înseamnă că deplasarea punctului P se produce în sens contrar celui al forţei (F).

4. Dacă se intenţionează a se calcula deplasarea unui punct Q în care nu există o forţă concentrată exterioară, atunci teorema se aplică după introducerea unei forţe axiale fictive (K) în acel punct, urmată de exprimarea tuturor elementelor de calcul (reacţiuni şi eforturi secţionale) în funcţie de (K). După efectuarea derivatelor parţiale ale eforturilor N(x) în raport cu acest (K), se fac înlocuirile în relaţia (5.36), dând forţei fictive valoarea reală K=0. (A se vedea aplicaţia de mai jos).

5. La solicitarea axială simplă, deplasarea lui P va fi egală cu a tuturor punctelor din secţiunea transversală care îl conţine.

Primele patru dintre aceste observaţii vor fi valabile şi pentru celelalte solicitări, inclusiv în calculele de la solicitările compuse.