A. Rezolvare pe baza teoremei lui Castigliano

Notăm cu A şi cu B punctele de pe axa barei (centrele de greutate) ale secţiunilor de calcul.

Pentru aplicarea teoremei este necesară existenţa, în punctele precizate, a unor forţe concentrate axiale, exprimate independent de celelalte forţe din sistem.

Din acest motiv se notează prin Q forţa (7F) din capătul liber al barei, iar în punctul B se introduce o forţă fictivă K (de mărime reală zero), alegându-i sensul către dreapta (fig.5.10).

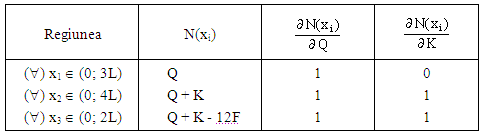
Regiunile de pe bară se iau la fel ca în aplicaţia precedentă, iar eforturile axiale şi derivatele lor parţiale în funcţie de forţele considerate vor fi următoarele:

Mai departe, deplasarea lui A se va obţine introducând în relaţia (5.36) termenii corespunzători forţei (Q) şi dând eforturilor axiale N(x_i) valoarea lor reală (obţinută pentru Q=7F şi K=0). Rezultă astfel că:

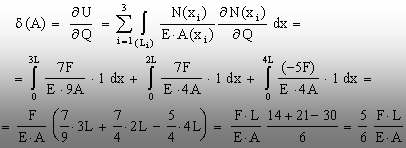(5.39)

Un calcul analog, în raport cu forţa (K), conduce la aflarea deplasării lui B:

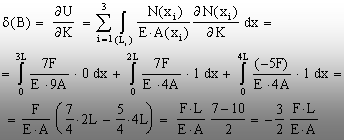(5.40)

Se poate observa cu uşurinţă că rezultatele obţinute coincid cu cele de la calculul prin metoda geometrică. Semnul negativ al deplasării lui B arată că secţiunea transversală cu centrul de greutate în acest punct se deplasează către stânga (în sens invers celui ales pentru forţa fictivă K), ceea ce s-a pus în evidenţă şi prin calculul făcut anterior.