Determinarea tensiunilor de pe secţiunile înclinate din barele drepte solicitate axial

Toate paragrafele anterioare au făcut referire la secţiuni transversale (obţinute prin “tăierea” barelor cu plane perpendiculare pe axa lor longitudinală). Este interesant de urmărit efectul produs de solicitările axiale în secţiunile înclinate faţă de cele transversale.

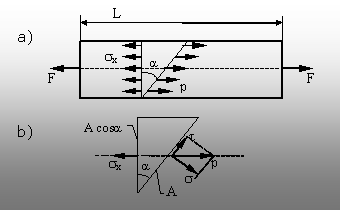
Se imaginează o bară prismatică, de lungime oarecare L, încărcată la capete cu forţele egale şi opuse F, în care se pune în evidenţă o secţiune arbitrară, plană şi înclinată sub unghiul a faţă de o secţiune transversală oarecare (fig. 5.12.a).

Se observă că, dacă se notează cu A mărimea ariei secţiunii înclinate, atunci secţiunea transversală a barei va avea aria (A×cosa).

Atenţie: Pe desen s-au reprezentat tensiunile s_x din secţiunea transversală, precum şi tensiunile (axiale) p care apar pe secţiunea înclinată!

Se separă, imaginar, un element din volumul barei, mărginit de cele două secţiuni citate şi de suprafaţa superioară a piesei (fig. 5.12.b), iar dimensiunea lui pe direcţie perpendiculară pe planul desenului se consideră a fi egală cu unitatea.

Fig. 5.12. Tensiunile de pe secţiuni înclinate la solicitarea axială.

Tensiunile s_x, s şi t conduc, ca efect global, la apariţia unor forţe rezultante care acţionează pe elementul de volum considerat şi care se află în echilibru, atât timp cât bara întreagă se află în echilibru.

Deoarece tensiunile sunt distribuite uniform pe suprafeţele pe care acţionează, oricare dintre forţele rezultante va fi egală cu produsul dintre valoarea tensiunii care îi corespunde şi mărimea suprafeţei pe care aceasta se repartizează.

Exprimarea matematică a acestei stări se face prin ecuaţiile de echilibru scrise pentru forţele rezultante ale tensiunilor menţionate, proiectate pe direcţia secţiunii înclinate considerate, respectiv pe normala la această suprafaţă, astfel:

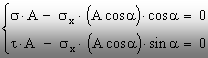
Deoarece aria A este o mărime strict pozitivă, se poate face împărţirea prin (A) a celor două ecuaţii de mai sus, după care cele două componente ale tensiunii (p) se vor scrie astfel:

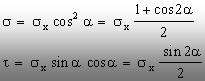(5.45)

Aceste expresii definesc componentele normală, respectiv tangenţială ale tensiunilor de pe o secţiune înclinată la unghiul a din volumul barei.

Dacă se analizează evoluţia acestor mărimi, atunci când unghiul a variază între valorile 0 (care corespunde unei secţiuni transversale a barei) şi (p/2) (secţiune longitudinală), se constată următoarele:

Þ Tensiunile normale s sunt maxime pe secţiunile transversale (unde s_max=s_x) şi scad în mod continuu la creşterea unghiului a, ajungând să se anuleze pe secţiunile longitudinale.

Þ Tensiunile tangenţiale t sunt nule pe secţiunile longitudinale şi transversale, având valoarea maximă (t_max=s_x/2) pe secţiunile înclinate la 45° faţă de secţiunile transversale ale barei.

Pe această bază se poate face încă o precizare importantă, confirmată de observaţiile experimentale:

Dacă ruperea unei bare se produce datorită atingerii limitei de rupere de către componentele s ale tensiunilor, atunci secţiunea de rupere va fi perpendiculară pe axa barei. Dacă se depăşeşte limita de rupere de către componentele tangenţiale t, atunci secţiunea de rupere va conţine suprafeţe înclinate la 45° faţă de secţiunile transversale ale barei.