2. Bare a căror dilatare termică este împiedicată

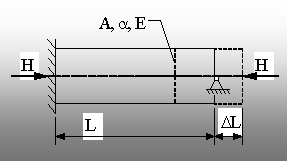
Fig. 5.18.

Se consideră (fig. 5.18) o bară prismatică (având lungimea L şi aria secţiunii transversale A), dintr-un metal cu modulul de elasticitate E şi coeficientul de dilatare termică liniară a.

Capetele barei sunt fixate, prin rezemare, împo-triva deplasărilor axiale.

Se imaginează că se aplică barei o creştere de temperatură (Dt), astfel că ea tinde să-şi mărească volumul, adică să se dilate. Dacă se presupune că dilatarea barei nu ar fi împiedicată şi că s-ar produce preponderent în direcţie axială (modificarea celorlalte dimensiuni fiind neglijabilă), atunci creşterea lungimii ei ar avea mărimea

(5.51)

În realitate, distanţa dintre capetele barei nu se poate modifica. Se poate imagina că acest lucru se întâmplă pentru că reazemele apasă asupra piesei cu forţe axiale H, care sunt egale între ele (conform ecuaţiei de echilibru al forţelor de pe direcţia axei) şi care produc comprimarea barei pe o distanţă (DL^m). Aceasta poate fi numită deformaţie mecanică şi calculată cu o relaţie de forma (5.10).

Observând că, pe toată lungimea barei, efortul axial este N(x)=H=ct.

se obţine:

(5.52)

Deoarece lungimea barei nu se schimbă după producerea încălzirii, rezultă că DL^t=DL^m, iar din egalitatea termenilor din partea dreaptă, din relaţiile (5.51) şi (5.52), se ajunge la determinarea forţei care solicită bara, după formula:

(5.53)

Atenţie: Trebuie remarcată lipsa lui L din această relaţie. Forţa H este constantă pentru toate secţiunile transversale şi nu este influenţată de lungimea barei!

Pe de altă parte, tensiunile din piesă sunt constante în întregul ei volum, având mărimea dată de relaţia:

(5.54)

Prin urmare, calculele de rezistenţă se vor baza pe inecuaţia următoare:

(5.55)

Din această condiţie se poate calcula, de exemplu, diferenţa de temperatură pe care o poate suporta o bară, în condiţii de siguranţă.

Exemplu: 5.6. Pentru o bară ca aceea din figura 5.18, cu E=2,1×10⁵ MPa, a=1,2×10^-5 grd^-1 şi s_a=150MPa, să se calculeze până la ce temperatură din timpul verii bara nu este periclitată, cunoscând că a fost instalată iarna, la temperatura de -20°C.

Rezolvare

Din relaţia (5.55) rezultă:

Prin urmare, bara poate suporta, în siguranţă, temperaturi de până la aproximativ 40°C. Dacă se doreşte creşterea temperaturii maxime, atunci trebuie schimbat materialul din care se confecţionează bara, alegând una sau mai multe dintre următoarele variante: rezistenţă admisibilă mai mare, modul de elasticitate mai mic, sau/şi coeficient de dilatare mai mic.

În final, trebuie observat faptul că în relaţia (5.55), pe care se bazează calculele de rezistenţă, nu apare nici una dintre dimensiunile barei, deci acestea nu influenţează în vreun fel comportarea piesei în condiţiile date!