Variantă a problemei precedente

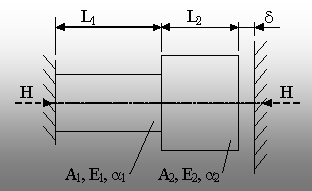
Fig. 5.19.

Se consideră o bară formată din două tronsoane de dimensiuni şi materiale diferite (fig. 5.19), având în plus şi lungimea totală ceva mai mică (cu intervalul d) decât distanţa dintre cei doi “pereţi” între care este montată.

Urmărind un raţio-nament similar celui de mai sus, dacă temperatura mediului creşte cu (Dt) grade, atunci dilatarea termică (liberă) a barei se poate calcula cu relaţia:

(5.56)

Se observă că, dacă această alungire este mai mică decât intervalul d, atunci bara nu va ajunge să atingă obstacolul din partea dreaptă, deci nu va fi solicitată din punct de vedere mecanic.

Din momentul atingerii acestuia, dilatarea barei nu va mai fi posibilă. Creşterea în continuare a temperaturii mediului va conduce la apariţia unei forţe de compresiune H în bară, având valoare constantă pe întreaga ei lungime (conform ecuaţiei de echilibru).

Prin urmare, pentru ca dilatarea să nu se producă, se poate spune că ea este compensată de o comprimare a celor două tronsoane, având valoarea:

(5.57)

Analizând desenul de mai sus, rezultă că:

(5.58)

iar pe baza ultimelor trei relaţii se poate determina valoarea forţei de compresiune care solicită bara, după formula:

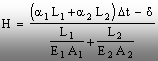(5.59)

Toate mărimile din membrul drept au valori cunoscute, deci calculul forţei H nu prezintă dificultăţi şi permite stabilirea tensiunilor mecanice din cele două tronsoane ale barei.

Pentru ca tensiunile să nu depăşească domeniul de funcţionare sigură şi stabilă, calculul de rezistenţă se face, fără dificultăţi deosebite, pe baza inecuaţiilor (5.60), care trebuie să fie adevărate simultan:

(5.60)

Pe de altă parte, se observă că problema ca tronsoanele barei să fie solicitate amândouă la capacitatea maximă de rezistenţă poate fi rezolvată numai în cazuri particulare de dimensionare a lor, ca şi de alegere a caracteristicilor fizice ale celor două materiale. De obicei, solicitarea la nivelul rezistenţei admisibile se realizează numai pentru unul dintre tronsoane, celălalt fiind “sub-solicitat”.