3. Bare cu secţiunea transversală neomogenă

Barele din această categorie sunt formate prin solidarizarea a două sau mai multe piese coaxiale, care de obicei sunt fabricate din materiale diferite şi participă în mod inegal la preluarea solicitărilor mecanice.

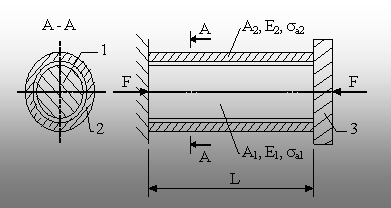
5.7. Se ia ca exemplu îmbinarea din figura 5.20, dintre o piesă plină 1 şi una tubulară 2, pentru care se cunosc elementele de calcul notate pe desen. Cele două piese sunt încastrate, la capătul din stânga, iar solidarizarea lor se realizează prin intermediul unei plăci rigide 3, asupra căreia acţionează forţa exterioară F. Se propune să se stabilească valorile tensiunilor care se produc în cele două piese.

Fig. 5.20.

Rezolvare

Din singura ecuaţie de echilibru semnificativă rezultă că în încastrare apare, ca reacţiune, o forţă egală cu F. Solicitarea din cele două piese va fi dată de eforturi de tip axial, care constituie necunoscutele problemei şi a căror sumă trebuie să fie F.

Prin urmare, dacă se fac notaţiile N(x₁)=N₁ N(x₂)=N₂

atunci se poate scrie că:

N₁ + N₂ = F (5.61)

Observaţie: Această egalitate se mai poate obţine, de exemplu, scriind ecuaţia de echilibru pentru toate forţele care acţionează asupra plăcii rigide din partea dreaptă.

Problema este simplu static nedeterminată, iar pentru a se ajunge la o a doua relaţie între forţele necunoscute trebuie remarcată egalitatea deformaţiilor produse în cele două piese în urma solicitării, din care urmează că

Se observă că fracţiile din ultima egalitate se împart prin (L), iar apoi se poate folosi o proprietate a şirurilor de rapoarte egale, precum şi ecuaţia (5.61), pe baza cărora se ajunge la următorul şir de egalităţi:

(5.62)

Egalând succesiv primul, respectiv al doilea raport din şirul de mai sus, cu ultimul, se pot determina tensiunile efective din cele două piese, care nu trebuie să depăşească rezistenţele admisibile ale celor două materiale:

(5.63)

Calculele de rezistenţă pentru cele două piese se vor face pe baza inecuaţiilor (5.63). Luând în considerare primul şi cel de-al treilea termen din fiecare dintre cele două expresii, se poate obţine raportul dintre tensiunile din cele două piese, sub forma următoare:

(5.64)

Această relaţie arată că valorile celor două tensiuni sunt inter-dependente, iar raportul lor are o valoare determinată de caracteristicile elastice ale celor două materiale.

Consecinţă importantă: Piesele considerate vor putea fi solicitate, simultan, la capacitatea maximă de rezistenţă numai în cazuri particulare, în care raportul rezistenţelor admisibile ale materialelor lor este egal cu cel al modulelor de elasticitate!