4. Sisteme de bare paralele

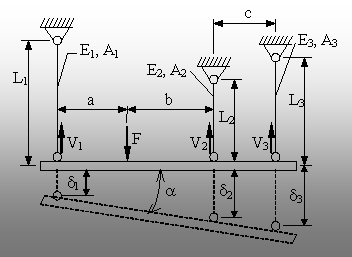
Fig. 5.21.

5.8. Se consideră o bară rigidă, suspendată în poziţie orizontală prin intermediul a trei tije verticale, de dimen-siuni şi din materiale diferite (fig. 5.21).

Dacă pe bara rigidă se aplică forţa verticală F, se cere să se determine valorile reacţiunilor care se produc în cele trei tije de sprijin.

Rezolvare

Desenul cu linii punctate din figura 5.21 prezintă, fără să respecte proporţiile fenomenelor reale (pentru că sunt reprezentate deformaţii exagerate ale tijelor), poziţia căpătată de bara rigidă în urma acţiunii forţei exterioare F.

S-au notat cu (d_i) deformaţiile tijelor, cu (V_i) – reacţiunile din tije, iar cu (a) – unghiul (necunoscut) cu care bara se înclină faţă de poziţia sa iniţială. Deoarece deformaţiile sunt de fapt foarte mici, în raport cu dimensiunile tijelor, se poate considera că tijele rămân verticale şi după aplicarea forţei F.

Toate forţele din problemă având direcţie verticală, rezultă că se pot scrie doar două ecuaţii de echilibru semnificative – suma forţelor verticale, respectiv suma de momente faţă de un punct din planul desenului (s-a ales punctul în care acţionează reacţiunea V₁), adică:

(5.65)

S-a obţinut un sistem de două ecuaţii, cu trei necunoscute, deci problema este simplu static nedeterminată.

Cea de-a treia ecuaţie de legătură între reacţiuni se poate obţine, de exemplu, observând că cele două poziţii ale barei rigide se află pe direcţia unei catete, respectiv a ipotenuzei, dintr-un triunghi dreptunghic imaginar, cu vârful în punctul de intersecţie a celor două direcţii.

Cum cele trei tije rămân verticale şi după deformarea lor, pe baza cunoştinţelor de geometrie elementară, referitoare la segmentele cuprinse între drepte paralele, se poate scrie că:

(5.66)

Observând că eforturile axiale din cele trei tije sunt egale cu reacţiunile V_i, rezultă că deformaţiile lor se vor putea calcula pe baza unor relaţii de forma:

Dacă se înlocuiesc aceste expresii în egalitatea (5.66), atunci se obţine o ecuaţie care are ca singure necunoscute reacţiunile V_i şi care, adăugată sistemului (5.65), conduce la rezolvarea nedeterminării din problema considerată.