5. Sisteme de bare concurente

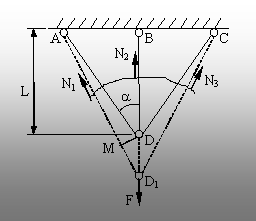
Fig. 5.22.

5.9. Se imaginează un sistem de trei bare, identice ca material şi secţiune transversală, dintre care una verticală, de lungime L şi alte două aşezate simetric, cu încli-nare la unghiul a (fig. 5.22).

Barele sunt articulate la capete şi concurente într-un punct D, în care acţionează forţa con-centrată F, de direcţie verticală.

Se propune să se deter-mine valorile eforturilor din cele trei bare.

Rezolvare

Pe desenul alăturat s-au reprezentat (exagerând mărimea deformaţiilor), cu linii întrerupte, poziţiile punctelor sistemului după aplicarea forţei F. Dacă se face o secţiune imaginară prin cele trei bare, atunci se pun în evidenţă eforturile axiale (N_i), singurele eforturi din barele sistemului (datorită prinderii lor articulate la ambele capete).

Deoarece forţele care apar în problemă se întâlnesc în punctul D₁, rezultă că echilibrul lor se poate scrie numai sub forma ecuaţiilor de forţe:

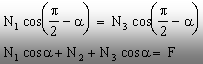(5.67)

Din prima ecuaţie rezultă egalitatea reacţiunilor din barele oblice N₁ = N₃, care se verifică şi prin simetria lor. Pe această bază, se poate constata că rămân de determinat două necunoscute, între care se cunoaşte o singură ecuaţie de legătură (cea de-a doua din sistemul de mai sus), care se scrie:

(5.68)

Problema este deci simplu static nedeterminată, iar cea de-a doua ecuaţie rezultă din observarea relaţiilor geometrice dintre segmentele de bară care formează triunghiul dreptunghic D₁MD. Deformaţiile barelor sunt foarte mici faţă de lungimile lor, astfel încât se poate considera că unghiurile dintre bare nu se modifică, în starea finală a sistemului.

Între laturile triunghiului citat există relaţia MD₁=D₁D cosa, iar segmentele care apar în această relaţie sunt egale cu deformaţiile barelor, astfel:

(5.69)

Din enunţul problemei rezultă că barele au aceeaşi rigiditate, iar segmentele din membrul drept al relaţiilor (5.69) au mărimile: AD=L/cosa şi BD=L.

Rezultă că relaţia dintre cele două alungiri se scrie

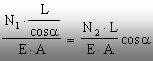
de unde se deduce o nouă ecuaţie de legătură între necunoscute:

(5.70)

Sistemul format din ecuaţiile (5.67) şi (5.70) permite rezolvarea nedeterminării problemei.

Atenţie: Rezolvarea se face identic în cazul în care barele oblice sunt diferite ca material şi arie transversală faţă de bara din mijloc!

Metoda prezentată este geometrică, iar aplicarea ei este indicată în cazurile în care barele sunt aşezate simetric, sau în care relaţiile dintre deformaţii pot fi obţinute cu uşurinţă. Pentru celelalte situaţii se folosesc metodele energetice de rezolvare a nedeterminărilor.